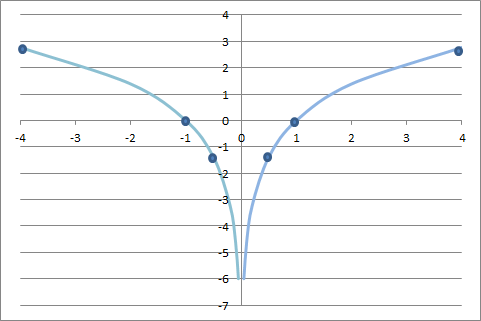
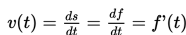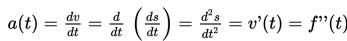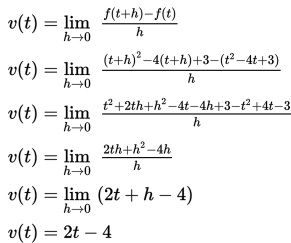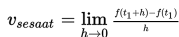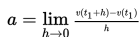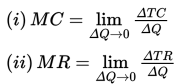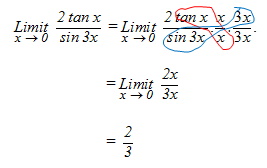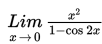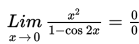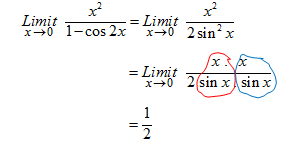Menggambarkan hubungan dengan grafik

Menggambarkan hubungan dengan grafik 

SOAL 1

Kamu menyewa mobil yang menempuh jarak 10 meter dalam satu jam. Temukan hubungan untuk menghitung jarak tempuh mobil selama "t" jam.

SOAL 2

Jika seorang penulis menulis 80 halaman dalam satu jam untuk sebuah novel, temukan jumlah total halaman yang ditulis dalam jam 't' jika 50 halaman ditulis oleh asistennya.

SOAL 3

Jika sebuah derek mengangkat 45 ton/jam untuk sekali kerjanya. Temukan  jumlah waktu yang diperlukan untuk mengangkat 750 ton jika 50 ton sudah diangkat sebelumnya sebelum derek mulai bekerja.

SOAL 4

Jika seorang sales berja selama 12 jam sehari, temukan jumlah total produk yang dijual setelah 30 hari jika dia menjual 10 produk / jam ditambah 50 produk gratis bulanan.

SOAL 5

Jika sebuah perusahaan membuat produk dengan biaya $5 dan biaya teknologi total untuk produknya adalah $650, grafik mana yang menggambarkan hubungan antara total pengeluaran y yang dibutuhkan untuk membuat produk sejumlah x?

SOAL 6

Seorang pria menyewa sebuah apartemen. Dia membayar biaya tunggal $1200 ditambah $250 per bulan. Grafik hubungan manakah yang paling bisa menggambarkan total pembayarannya?

SOAL 7

Keuntungan dari suatu perusahaan dihitung dengan bentuk:

P=x2+2x+4

mana x adalah jumlah produk yang dijual oleh perusahaan. Jika keuntungannya enam kali jumlah produk, berapakah kuantitas produk yang dijual?

SOAL 8

Sebuah perusahaan telepon awalnya membebankan $400 untuk sambungan dan kemudian membebankan biaya sewa $45 per bulan. Manakah yang menggambarkan hubungan antara total pembayaran dan jumlah bulan, t?

SOAL 9

Berat truk yang dimuati dengan n objek, dalam kg, adalah 

W=150n+4500

Jika sebuah jembatan mempunyai batas beban 6000kg, berapa banyak objek yang bisa truk muat tanpa menyebabkan kerusakan pada jembatan?

SOAL 10

Hubungan untuk kurva permintaan dan kurva penawaran dari perusahaan dinyatakan dengan

Qd=1400-80P

Qs=400+45P
dimana Qd adalah jumlah permintaaan sedangkan Qs adalah jumlah yang ditawarkan. Manakah yang merupakan titik keseimbangannya?

Grafik Fungsi Eksponensial dan Logaritma

Grafik Fungsi Eksponensial dan Logaritma

SOAL 1

Identifikasilah grafik fungsi logaritma f(x) = ln (-x)

SOAL 2

Identifikasilah grafik fungsi eksponensial f(x) = e (x + 2)

SOAL 3

Dari grafik berikut ini, manakah yang merepresentasikan fungsi eksponensial f(x) = -e -x

?

SOAL 4

Dari grafik berikut ini, manakah yang merepresentasikan fungsi logaritma f(x) = ln (x - 1) + 1
?

SOAL 5

Identifikasilah grafik fungsi logaritma berikut ini : f(x) = -ln (-x + 1)

SOAL 6

Fungsi eksponensial f(x) = -e (-x - 1) + 1   direpresentasikan oleh grafik berikut ini :

SOAL 7

Dari grafik berikut ini, manakah yang merepresentasikan f(x), jika diketahui :

             f (x) = -3 ln (x - 4)

SOAL 8

Dari pilihan di bawah ini, grafik manakah yang merepresentasikan f(x) f(x) 

              jika diketahui :  f (x) = 3(x + 1) - 2

 SOAL 9

Dari pilihan berikut ini, fungsi manakah yang merepresentasikan grafik di bawah ini?

SOAL 10

Grafik yang merepresentasikan fungsi f(x) = log2 (x + 2) adalah :

Nilai fungsi dan nilai akar-akar persamaan aljabar

Nilai fungsi dan nilai akar-akar persamaan aljabar - Kalian tentu sudah memahami tentang konsep dan sifat turunan fungsi, bukan?

Pada topik ini kalian akan belajar tentang penerapan konsep dan sifat turunan fungsi dalam menentukan nilai fungsi dan akar-akar persamaan aljabar.

Salah satu dari terapan konsep turunan fungsi yang berkaitan dengan nilai fungsi dan akar-akar persamaan aljabar adalah tentang gerak rektilinear. Gerak rektilinear adalah gerakan sebuah partikel di sepanjang garis lurus. Persamaan gerak sebuah partikel dinyatakan dengan s = f (t) , dimana

• s adalah panjang lintasan atau jarak (dalam satuan panjang)
• t adalah waktu (dalam satuan waktu)

Macam-macam gerak rektilinear antara lain :

• Kecepatan dan laju
• Percepatan

Kecepatan v(t) pada saat waktu t adalah

Kecepatan gerak sebuah partikel merupakan turunan pertama dari panjang lintasan terhadap waktu.

Percepatan v(t) pada saat waktu t adalah

Percepatan gerak partikel merupakan turunan pertama dari kecepatan terhadap waktu atau turunan kedua dari panjang lintasan terhadap waktu. Selain dalam gerak rektilinear, konsep turunan dapat juga digunakan dalam menentukan laju perubahan luas terhadap panjang sisi atau jari-jari, laju perubahan volume terhadap panjang sisi atau jari-jari.

Agar lebih jelas, mari kita perhatikan contoh-contoh berikut ini.

Contoh 1:

Sebuah partikel bergerak sepanjang lintasan dengan posisi memenuhi persamaan 
s = f(t) = t2 – 4t + 3, t ≥ 0, dengan s dalam meter dan t dalam detik.

a) Tentukan kecepatan gerak partikel pada saat t = 3 detik.
b) Tentukan percepatan gerak partikel

Penyelesaian :

Kecepatan gerak partikel pada saat t detik dapat ditentukan dengan cara berikut :

Berdasarkan uraian di atas, kecepatan gerak partikel pada saat t = 3 detik adalah
v(3) = 2(3) – 4 = 2. Dengan kata lain, kecepatan pada saat t = 3 detik adalah 2 m/det.

Selanjutnya, karena percepatan merupakan turunan pertama dari kecepatan, maka
a(t) = v’(t) = 2. Dengan demikian, percepatan gerak partikel dalam kasusu ini adalah konstan, yaitu 2 m/det2

Contoh 2 :

Sebuah partikel bergerak di sepanjang suatu garis lurus dengan persamaan 
s = f(t) = 2t3 – 9t2 + 12t – 1. Tentukan waktu dimana pertikel berhenti, dan kemudian bergerak lagi!

Penyelesaian :

Karena kecepatan adalah turunan pertama dari fungsi jarak, maka

v(t) = f’(t) 
<=> v(t) = 6t2 – 18t + 12

Karena partikel berhenti kemudian bergerak lagi bila kecepatan nol, maka

v(t) = 0
<=> 6t2 – 18t + 12 = 0
<=> t2 – 3t + 2 = 0
<=> (t – 1)(t – 2) = 0
<=> t = 1 atau t = 2

Jadi, partikel berhenti kemudian bergerak lagi pada waktu t = 1 atau t = 2.

Masalah nyata yang berkaitan dengan turunan fungsi trigonometri

Masalah nyata yang berkaitan dengan turunan fungsi trigonometri - Pada topik sebelumnya kalian telah belajar tentang konsep turunan fungsi aljabar dan fungsi trigonometri. Kalian juga telah belajar menerapkan konsep turunan fungsi aljabar untuk masalah nyata maupun masalah matematika.

Apakah kalian masih ingat terapan konsep turunan digunakan untuk apa?

Penerapan konsep turunan antara lain dipakai untuk :
1) menentukan persamaan garis singgung kurva
2) menentukan interval dimana fungsi naik dan interval dimana fungsi turun
3) menentukan menyelesaikan masalah-masalah ekstrim
4) menentukan gerak rektilinear (kecepatan dan percepatan pada gerak lurus)
5) perhitungan pada limit fungsi

Nah, pada topik kali ini, kalian akan belajar menyelesaikan masalah-masalah nyata yang berkaitan dengan turunan fungsi trigonometri.

Dalam hal ini, tentu kalian harus ingat turunan fungsi trigonometri, antara lain :

1. turunan fungsi y = sin x adalah y’ = cos x
2. turunan fungsi y = cos x adalah y’ = - sin x
3. turunan fungsi y = tan x adalah y’ = sec2 x, dan seterusnya.

Agar lebih jelas mari kita perhatikan contoh berikut ini.

Contoh :

Sebuah tangga panjangnya 8 meter bersandar pada dinding tegak yang tingginya 6 meter dengan bagian atas tangga melewati dinding. Jika ujung bawahnya ditarik horizontal dengan kecepatan 2 meter/detik menjauhi dinding, tentukan kecepatan vertikal ujung atas tangga pada saat tangga membentuk sudut 60o dengan permukaan lantai.

Penyelesaian :

Perhatikan gambar berikut :

Misalkan pada saat t, sudut antara tangga dengan permukaan lantai adalah ϴ, jarak ujung bawah tangga ke dinding adalah x meter, dan jarak ujung atas tangga ke permukaan lantai adalah y meter.

Oleh karena kecepatan vertikal ujung atas tangga ditanyakan, maka kita perlu menentukan dy/dt pada saat tangga membentuk sudut 60o dengan permukaan lantai dan dx/dt = 2 m/det.

Berdasarkan gambar di atas,

Turunan implisit terhadap t dari kedua ruas menghasilkan

Untuk ϴ = 60o berlaku :

Jika hasil di atas disubtitusikan ke persamaan (*), maka diperoleh hasil sebagai berikut :

Jika kita melihat gambar di atas lagi, maka diperoleh

Turunan implisit terhadap t dari kedua ruas menghasilkan

(tanda negatif menunjukkan arah ke bawah)

Dengan demikian, kecepatan vertikal ujung atas tangga adalah -1 m/det .

Penerapan turunan fungsi trigonometri untuk menentukan titik Stasioner

Penerapan turunan fungsi trigonometri untuk menentukan titik Stasioner - Pada materi turunan fungsi aljabar kita telah mempelajari bagaimana cara menentukan titik-titik stasioner, yaitu dengan syarat f’(x) = 0. Demikian pula halnya cara menentukan titik-titik stasioner dari fungsi trigonometri yang akan kita pelajari ini, pada prinsipnya sama seperti cara menentukan titik-titik stasioner dari fungsi aljabar.

Setelah kalian paham cara menurunkan fungsi trigonometri, sekarang kita akan menerapkannya untuk menentukan titik-titik stasioner (titik maximum, titik minimum dan titik belok), menentukan interval fungsi naik dan fungsi turun serta menentukan persamaan garis singgung dari fungsi trigonometri.

Agar lebih jelas, mari kita cermati beberapa contoh berikut ini.

Contoh 1 :

Tentukan titik stasioner dan jenisnya dari fungsi : f(x) = sin x + cos x, untuk 0o ≤ x ≤ 360o

Penyelesaian :

Kita ingat pada fungsi aljabar bahwa titik stasioner dicapai jika turunannya adalah nol, demikian juga untuk fungsi trigonometri, titik stasioner dicapai juga jika turunannya sama dengan nol.

Jadi titik stasioner untuk fungsi di atas adalah

Untuk menentukan jenis titik stasioner, kita gunakan pertolongan garis bilangan :

Jadi jenis titik (45o, √2) adalah titik balik maksimum dan titik (225o, -√2) adalah titik balik minimum.

Contoh 2 :

Tentukan interval fungsi naik dan fungsi turun dari fungsi f(x) = √3 cos x – sin x, untuk 0 ≤ x ≤ 2π

Penyelesaian :

Seperti pada fungsi aljabar, bahwa fungsi akan naik jika f’(x) > 0 dan fungsi akan turun jika f’(x) < 0.

Jadi fungsi naik untuk interval 5/6 π < x < 11/6 π

Syarat fungsi turun => f’(x) < 0
Jadi fungsi turun untuk interval 0 < x < 5/6 π atau 11/6 π < x < 2π.

Contoh 3 :

Tentukan persamaan garis singgung kurva y = √3 sin x – cos x di titik (1/3 π,1).

Penyelesaian :

Sebelum menentukan persamaan garis singgung suatu kurva kita cari dulu gradien dari fungsi tersebut dengan cara menentukan turunan fungsinya.

Jadi persamaan garis singgung di titik (1/3 π,1) adalah :

Turunan Fungsi Trigonometri

Turunan Fungsi Trigonometri - Dalam topik sebelumnya kita telah mempelajari limit fungsi trigonometri dan Konsep Turunan Fungsi Aljabar. Turunan dari fungsi aljabar menghasilkan fungsi aljabar, begitu pula halnya dengan turunan dari fungsi trigonometri ternyata hasilnya juga merupakan fungsi trigonometri. Nah, dalam topik ini, kalian akan belajar tentang turunan fungsi trigonometri.

Mari kita ingat kembali materi pada topik sebelumnya.

Rumus Turunan Fungsi Aljabar

Teknis Perhitungan Limit Fungsi Trigonometri

Untuk menentukan turunan fungsi trigonometri pada prinsipnya sama dengan menentukan turunan fungsi aljabar, yaitu menggunakan definisi turunan atau rumus umum turunan fungsi f(x), yaitu

Contoh 1 :

Tentukan turunan fungsi f(x) = sin x !

Penyelesaian :

Berdasarkan definisi turunan, diperoleh hasil sebagai berikut :

Jadi, turunan fungsi f(x) = sin x adalah f’(x) = cos x.

Dengan cara yang sama seperti pada contoh di atas, cobalah menentukan turunan fungsi

f(x) = cos x

Contoh 2 :

Tentukan turunan pertama dari f(x) = tan x !

Penyelesaian :

Jadi, turunan pertama fungsi f(x) = tan x adalah f’(x) = sec2x.

Contoh 3 :

Tentukan turunan pertama f(x) = 2 sin x + 3 cos x !

Penyelesaian :

Oleh karena f(x) = 2 sin x + 3 cos x mempunyai bentuk yang sama dengan f(x) = u(x) + v(x), maka turunan pertamanya adalah f’(x) = 2 cos x – 3 sin x.

Contoh 4 :

Tentukan turunan pertama f(x) = sin2 x !

Penyelesaian :

Oleh karena f(x) = sin2 x mempunyai bentuk yang sama dengan f(x) = {u(x)}n, maka 
f’(x) = 2 sin x cos x

Contoh 5 :

Tentukan turunan pertama f(x) = x3 cos x !

Penyelesaian :

Oleh karena f(x) = x3 cos x mempunyai bentuk yang sama dengan f(x) = u(x).v(x), maka

Contoh 6 :

Tentukan turunan pertama f(x) = 4 cos3 (2x – 5) !

Penyelesaian :

Oleh karena f(x) = 4 cos3 (2x – 5) mempunyai bentuk yang sama dengan f(x) = {u(x)}n, maka

Contoh 7 :

Jika f(x) = 4 cos x – 2 sin x, tentukan nilai dari f’(3/4 π) !

Jawab :

Contoh 8 :

Hitung nilai f'(π/6) jika diketahui

Hitung nilai f’(1/6 π)

Penyelesaian :

Setelah kita perhatikan beberapa contoh di atas, tentunya kalian sudah paham tentang turunan fungsi trigonometri bukan?

Konsep limit dalam konteks nyata

Konsep limit dalam konteks nyata - Pada topik sebelumnya, kalian telah belajar mengenal konsep limit fungsi, sedangkan dalam topik ini kalian akan belajar tentang penerapan konsep limit dalam konteks nyata.

Mari kita ingat kembali konsep limit fungsi.

Pengertian Limit

Limit berarti pendekatan. Limit fungsi f(x) untuk x mendekati c sama artinya dengan pendekatan nilai f(x) untuk x = c. Selanjutnya, limit fungsi ini ditulis seperti berikut :

Secara intuitif, jika f : R → R , L dan c merupakan bilangan real, maka berlaku hubungan sebagai berikut :

Apakah kalian masih ingat dengan limit kanan dan limit kiri?

Limit Kanan

Limit Kiri

Jika diberikan fungsi f : R → R dengan L dan c bilangan real, maka berlaku pula konsep limit kanan dan limit kiri berikut ini :

Selanjutnya, untuk menyelesaikan limit fungsi aljabar, digunakan metode berikut :

• substitusi langsung
• faktorisasi
• menyederhanakan

Limit Fungsi di tak hingga

Limit fungsi f(x) untuk x mendekati tak hingga ditulis seperti berikut :

Seperti yang telah kalian ketahui, dalam limit fungsi di tak hingga, berlaku hubungan sebagai berikut :

Adapun cara untuk menyelesaikan limit fungsi di tak hingga adalah sebagai berikut :

Sifat - Sifat Limit

Konsep limit dalam konteks nyata diantaranya dapat dijumpai dalam bidang fisika dan ekonomi.

Penerapan limit dalam bidang fisika

Kecepatan sesaat adalah limit dari kecepatan ata-rata dan dapat dinyatakan seperti berikut ini :

Percepatan gerak benda adalah limit dari percepatan rata-rata dan dinyatakan seperti berikut

Penerapan limit dalam bidang ekonomi

Konsep limit dalam bidang ekonomi sering digunakan untuk menentukan biaya marjinal (marginal cost) dan penerimaan marjinal (marginal revenue).

Biaya marjinal adalah laju perubahan sesaat biaya terhadap banyaknya barang yang dihasilkan, sedangkan penerimaan marjinal adalah laju perubahan sesaat penerimaan terhadap banyaknya barang yang dihasilkan.

Biaya marjinal dan penerimaan marjinal dinyatakan sebagai berikut :

Mari kita cermati contoh berikut ini.

Contoh :

Seutas tali dengan panjang satu satuan panjang, dipotong menjadi 2 bagian yang sama, lalu ½ bagian dari tali itu dibagi 2 lagi, kemudian ¼ bagian dari tali itu dipotong menjadi 2 lagi, dan seterusnya. Apa yang dapat kamu simpulkan?

Penyelesaian :

Jika tali tersebut dipotong terus menerus, dengan panjang potongan berikutnya adalah setengah kali potongan semula, maka berdasarkan nilai limit di atas, tali tersebut pada akhirnya akan habis dan tidak lagi dapat dipotong.

Limit Fungsi Trigonometri dan Limit Fungsi Aljabar untuk x -> ~

Limit Fungsi Trigonometri dan Limit Fungsi Aljabar untuk x -> ~ Pada topik ini kalian akan belajar tentang 2 materi sekaligus, yaitu limit fungsi trigonometri dan limit fungsi aljabar untuk x -> ~

Limit Trigonometri

Untuk mempelajari limit fungsi trigonometri, tentunya kalian harus ingat rumus-rumus trigonometri yang nantinya akan sering digunakan.

Mari kita ingat kembali rumus-rumus trigonometri berikut :

Pengertian

Limit fungsi trigonometri adalah limit yang memuat perbandingan trigonometri.

Bentuk umum penulisan

dengan f(x) adalah fungsi yang memuat perbandingan trigonometri

Rumus-rumus limit fungsi trigonometri

Untuk cosinus tidak berlaku seperti rumus di atas

Contoh 1

Hitung nilai dari

Penyelesaian :

Jika kita substitusikan nilai x = 0, maka diperoleh :

Agar tidak diperoleh bentuk 0/0, maka untuk menyelesaikannya kita gunakan rumus trigonometri sebagai berikut :

Contoh 2

Hitung nilai

Penyelesaian :

Jika kita substitusikan x = 0, maka diperoleh :

agar tidak diperoleh bentuk 0/0, maka digunakan rumus cos 2x = 1 – 2 sin2 x

Contoh 3

Hitung nilai

Penyelesaian :

Jika kita substitusikan x = 0, maka diperoleh :

agar tidak diperoleh bentuk 0/0, maka digunakan rumus

sehingga diperoleh :

Limit Fungsi Aljabar untuk x -> ~

Pengertian

Limit fungsi aljabar untuk x -> ~ adalah limit dengan nilai x mendekati tak hingga.

Mari kita perhatikan tabel berikut :

Dari tabel di atas, terlihat bahwa untuk nilai x mendekati tak hingga diperoleh nilai 1/x mendekati 0.

Dengan demikian,

Cara menyelesaikan limit fungsi aljabar untuk x -> ~

Jika fungsi berbentuk f(x) ± g(x) dengan f(x) dan g(x) masing-masing fungsi irasional (bentuk akar), maka penyelesaian dengan cara mengalikan dengan sekawan dari bentuk f(x) ± g(x), kemudian dilanjutkan dengan cara seperti no. 1 di atas.

Contoh 4

Penyelesaian :

Contoh 5

Penyelesaian :

Contoh 6

Penyelesaian :

Contoh 7

Penyelesaian :

Contoh 8

Penyelesaian :

Dari beberapa contoh di atas, dapat kita simpulkan bahwa langkah-langkah menghitung nilai limit untuk x -> ~ dapat disesuaikan dengan bentuk fungsi limitnya :

1. Jika n = m, maka nilai h = a/p
2. Jika n < m, maka nilai h = 0
3. Jika n > m, maka nilai h = ~

1. Jika a = p, maka nilai h = 0
2. Jika a < p, maka nilai h = - ~
3. Jika a > p, maka nilai h = ~

a. Jika a = p, maka nilai h = (b - q) / 2√a
b. Jika a < p, maka nilai h = - ~
c. Jika a > p, maka nilai h = ~

Contoh 9

Hitung nilai

Penyelesaian :

Contoh 10

Hitung nilai

Penyelesaian :

Contoh 11

Penyelesaian :

Karena a = p maka