Turunan Fungsi Trigonometri

Turunan Fungsi Trigonometri - Dalam topik sebelumnya kita telah mempelajari limit fungsi trigonometri dan Konsep Turunan Fungsi Aljabar. Turunan dari fungsi aljabar menghasilkan fungsi aljabar, begitu pula halnya dengan turunan dari fungsi trigonometri ternyata hasilnya juga merupakan fungsi trigonometri. Nah, dalam topik ini, kalian akan belajar tentang turunan fungsi trigonometri.

Mari kita ingat kembali materi pada topik sebelumnya.

Rumus Turunan Fungsi Aljabar

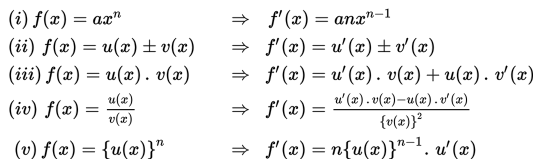
Teknis Perhitungan Limit Fungsi Trigonometri

Untuk menentukan turunan fungsi trigonometri pada prinsipnya sama dengan menentukan turunan fungsi aljabar, yaitu menggunakan definisi turunan atau rumus umum turunan fungsi f(x), yaitu

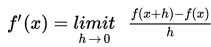
Contoh 1 :

Tentukan turunan fungsi f(x) = sin x !

Penyelesaian :

Berdasarkan definisi turunan, diperoleh hasil sebagai berikut :

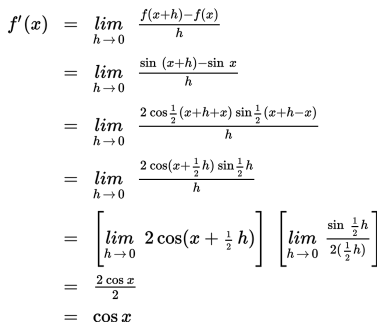
Jadi, turunan fungsi f(x) = sin x adalah f’(x) = cos x.

Dengan cara yang sama seperti pada contoh di atas, cobalah menentukan turunan fungsi

f(x) = cos x

Contoh 2 :

Tentukan turunan pertama dari f(x) = tan x !

Penyelesaian :

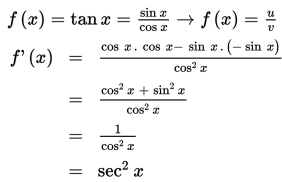
Jadi, turunan pertama fungsi f(x) = tan x adalah f’(x) = sec2x.

Contoh 3 :

Tentukan turunan pertama f(x) = 2 sin x + 3 cos x !

Penyelesaian :

Oleh karena f(x) = 2 sin x + 3 cos x mempunyai bentuk yang sama dengan f(x) = u(x) + v(x), maka turunan pertamanya adalah f’(x) = 2 cos x – 3 sin x.

Contoh 4 :

Tentukan turunan pertama f(x) = sin2 x !

Penyelesaian :

Oleh karena f(x) = sin2 x mempunyai bentuk yang sama dengan f(x) = {u(x)}n, maka 
f’(x) = 2 sin x cos x

Contoh 5 :

Tentukan turunan pertama f(x) = x3 cos x !

Penyelesaian :

Oleh karena f(x) = x3 cos x mempunyai bentuk yang sama dengan f(x) = u(x).v(x), maka

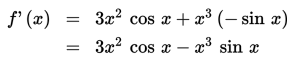
Contoh 6 :

Tentukan turunan pertama f(x) = 4 cos3 (2x – 5) !

Penyelesaian :

Oleh karena f(x) = 4 cos3 (2x – 5) mempunyai bentuk yang sama dengan f(x) = {u(x)}n, maka

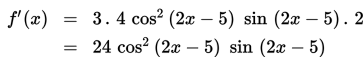
Contoh 7 :

Jika f(x) = 4 cos x – 2 sin x, tentukan nilai dari f’(3/4 π) !

Jawab :

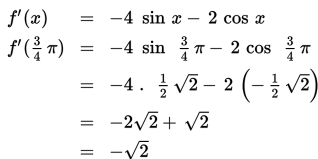
Contoh 8 :

Hitung nilai f'(π/6) jika diketahui

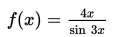
Hitung nilai f’(1/6 π)

Penyelesaian :

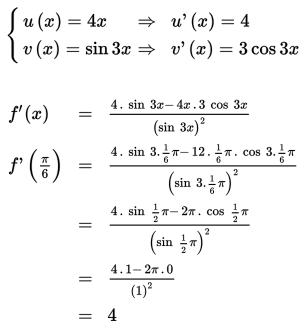
Setelah kita perhatikan beberapa contoh di atas, tentunya kalian sudah paham tentang turunan fungsi trigonometri bukan?