Pada topik ini kalian akan belajar tentang penerapan konsep dan sifat turunan fungsi dalam menentukan nilai fungsi dan akar-akar persamaan aljabar.
Salah satu dari terapan konsep turunan fungsi yang berkaitan dengan nilai fungsi dan akar-akar persamaan aljabar adalah tentang gerak rektilinear. Gerak rektilinear adalah gerakan sebuah partikel di sepanjang garis lurus. Persamaan gerak sebuah partikel dinyatakan dengan s = f (t) , dimana
- s adalah panjang lintasan atau jarak (dalam satuan panjang)
- t adalah waktu (dalam satuan waktu)
Macam-macam gerak rektilinear antara lain :
- Kecepatan dan laju
- Percepatan
Kecepatan v(t) pada saat waktu t adalah
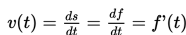
Kecepatan gerak sebuah partikel merupakan turunan pertama dari panjang lintasan terhadap waktu.
Percepatan v(t) pada saat waktu t adalah
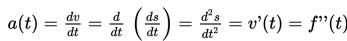
Percepatan gerak partikel merupakan turunan pertama dari kecepatan terhadap waktu atau turunan kedua dari panjang lintasan terhadap waktu. Selain dalam gerak rektilinear, konsep turunan dapat juga digunakan dalam menentukan laju perubahan luas terhadap panjang sisi atau jari-jari, laju perubahan volume terhadap panjang sisi atau jari-jari.
Agar lebih jelas, mari kita perhatikan contoh-contoh berikut ini.
Contoh 1:
Sebuah partikel bergerak sepanjang lintasan dengan posisi memenuhi persamaan
s = f(t) = t2 – 4t + 3, t ≥ 0, dengan s dalam meter dan t dalam detik.
s = f(t) = t2 – 4t + 3, t ≥ 0, dengan s dalam meter dan t dalam detik.
a) Tentukan kecepatan gerak partikel pada saat t = 3 detik.
b) Tentukan percepatan gerak partikel
b) Tentukan percepatan gerak partikel
Penyelesaian :
Kecepatan gerak partikel pada saat t detik dapat ditentukan dengan cara berikut :
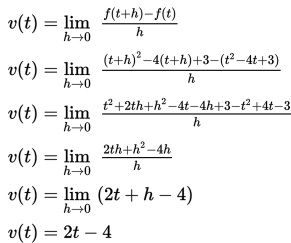
Berdasarkan uraian di atas, kecepatan gerak partikel pada saat t = 3 detik adalah
v(3) = 2(3) – 4 = 2. Dengan kata lain, kecepatan pada saat t = 3 detik adalah 2 m/det.
v(3) = 2(3) – 4 = 2. Dengan kata lain, kecepatan pada saat t = 3 detik adalah 2 m/det.
Selanjutnya, karena percepatan merupakan turunan pertama dari kecepatan, maka
a(t) = v’(t) = 2. Dengan demikian, percepatan gerak partikel dalam kasusu ini adalah konstan, yaitu 2 m/det2
a(t) = v’(t) = 2. Dengan demikian, percepatan gerak partikel dalam kasusu ini adalah konstan, yaitu 2 m/det2
Contoh 2 :
Sebuah partikel bergerak di sepanjang suatu garis lurus dengan persamaan
s = f(t) = 2t3 – 9t2 + 12t – 1. Tentukan waktu dimana pertikel berhenti, dan kemudian bergerak lagi!
s = f(t) = 2t3 – 9t2 + 12t – 1. Tentukan waktu dimana pertikel berhenti, dan kemudian bergerak lagi!
Penyelesaian :
Karena kecepatan adalah turunan pertama dari fungsi jarak, maka
v(t) = f’(t)
<=> v(t) = 6t2 – 18t + 12
<=> v(t) = 6t2 – 18t + 12
Karena partikel berhenti kemudian bergerak lagi bila kecepatan nol, maka
v(t) = 0
<=> 6t2 – 18t + 12 = 0
<=> t2 – 3t + 2 = 0
<=> (t – 1)(t – 2) = 0
<=> t = 1 atau t = 2
<=> 6t2 – 18t + 12 = 0
<=> t2 – 3t + 2 = 0
<=> (t – 1)(t – 2) = 0
<=> t = 1 atau t = 2
Jadi, partikel berhenti kemudian bergerak lagi pada waktu t = 1 atau t = 2.