Rotasi Sejauh Sudut Tertentu terhadap Pusat O(0,0)

Rotasi Sejauh Sudut Tertentu terhadap Pusat O(0,0) - Dalam topik ini kalian akan belajar tentang rotasi dengan titik pusat rotasi adalah O(0, 0).

Nah, tahukah kalian apa yang dimaksud dengan rotasi?

Jika kalian perhatikan, banyak hal dalam kehidupan sehari-hari yang berhubungan dengan rotasi. Sebagai contoh pergerakan jarum jam, gerakan roda mobil pada pusatnya, gerakan mata bor, dan gerakan melingkar pada sikat gigi listrik.

Dengan demikian, rotasi atau perputaran adalah gerakan memutar setiap titik pada suatu bidang terhadap titik tertentu yang selanjutnya disebut sebagai titik pusat rotasi. Adapun jarak antara titik semula dan titik pusat rotasi sama dengan jarak antara titik hasil rotasi dan titik pusat rotasi.

Coba tebak, unsur-unsur apa sajakah yang menentukan rotasi?

Ya, ada tiga unsur penentu dalam rotasi, yaitu: titik pusat rotasi, besar sudut rotasi, dan arah sudut rotasi.

Perlu kalian ketahui, jika arah sudut rotasi berlawanan arah dengan arah putar jarum jam, maka sudut rotasi dipandang sebagai sudut positif. Dengan kata lain, jika arah perputaran searah dengan arah putar jarum jam, maka sudut rotasi dipandang sebagai sudut negatif.

Mari kita perhatikan gambar berikut:

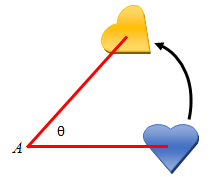
Pada gambar di atas, bangun berwarna biru dirotasikan sejauh θ dengan arah rotasi berlawanan arah dengan arah jarum jam dan pusat rotasi adalah titik A. Adapun hasil rotasi dari bangun berwarna biru adalah bangun berwarna kuning.

Apa yang dapat kalian simpulkan dari gambar di atas?

Ya, hasil rotasi tidak mengubah bentuk maupun ukuran.

Konsep Dasar

Untuk membantu pemahaman kalian mengenai konsep rotasi, mari kita cermati gambar berikut:

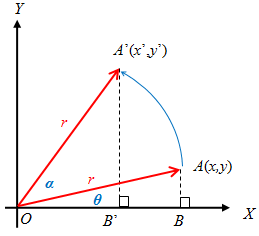
Pada gambar di atas, titik A(x, y) dirotasikan dengan pusat O(0, 0) sejauh α$\alpha$ dengan arah rotasi berlawanan arah dengan arah putar jarum jam. Adapun hasil rotasinya adalah titik A’(x’, y’).

Nah, berdasarkan gambar di atas, kita akan menyelidiki hubungan antara titik A dan A'.

Perhatikan ∆OAB.

Jika kita gunakan perbandingan trigonometri, maka kita peroleh hasil sebagai berikut:

• OB = r cos θ ⇔ x = r cos θ ... (1)
• OA = r sin θ ⇔ y = r sin θ ... (2)

Perhatikan ∆OA'B'.

Jika kita gunakan perbandingan trigonometri serta menerapkan hasil yang diperoleh dari persamaan (1) dan (2), maka kita peroleh hasil sebagai berikut:

OB⇔x′⇔x′⇔x′⇔x′=====r cos (θ+α)r cos (θ+α)r(cosθcosα−sinθsinα)(rcosθ)cosα−(rsinθ)sinαxcosα−ysinα  $\begin{array}{lll}OB& =& r\cos (\theta +\alpha )\\ \iff x^{\prime }& =& r\cos (\theta +\alpha )\\ \iff x^{\prime }& =& r(\cos \theta \cos \alpha -\sin \theta \sin \alpha )\\ \iff x^{\prime }& =& (r\cos \theta )\cos \alpha -(r\sin \theta )\sin \alpha \\ \iff x^{\prime }& =& x\cos \alpha -y\sin \alpha \end{array}$

OA′⇔y′⇔y′⇔y′⇔y′=====rsin(θ+α)rsin(θ+α)r(sinθcosα+cosθsinα)(rsinθ)cosα+(rcosθ)sinαycosα+xsinα  $\begin{array}{lll}O{A}^{\prime }& =& r\sin (\theta +\alpha )\\ \iff y^{\prime }& =& r\sin (\theta +\alpha )\\ \iff y^{\prime }& =& r(\sin \theta \cos \alpha +\cos \theta \sin \alpha )\\ \iff y^{\prime }& =& (r\sin \theta )\cos \alpha +(r\cos \theta )\sin \alpha \\ \iff y^{\prime }& =& y\cos \alpha +x\sin \alpha \end{array}$

Berdasarkan uraian di atas, dapat kita simpulkan bahwa hubungan antara titik A(x, y) dan A'(x', y') adalah sebagai berikut:

A(x,y)−→−−−−−−R(O(0,0),α)A′(x′,y′)=(xcosα−ysinα,xsinα+ycosα) $A(x,y)\stackrel{R(O(0,0),\alpha )}{\to }{A}^{\prime }(x^{\prime },y^{\prime })=(x\cos \alpha -y\sin \alpha ,x\sin \alpha +y\cos \alpha )$

Adapun persamaan matriks yang bersesuaian adalah sebagai berikut:

(x′y′ )=(cosαsinα−sinαcosα )(xy ) $\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{cc}\cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)$

Nah, apakah kalian sudah paham dengan materi di atas?

Mari kita cermati beberapa contoh berikut agar kalian semakin paham.

Contoh 1

Diketahui ∆ABC adalah segitiga siku-siku seperti pada gambar berikut.

Tentukan bayangan ∆ABC apabila dirotasikan sejauh π2 $\frac{\pi }{2}$ radian dengan pusat A dan arah rotasi searah putaran jarum jam.

Penyelesaian:

Jika kita misalkan hasil rotasi titik B dan C terhadap rotasi dalam soal adalah B' dan C', maka bayangan ∆ABC dapat kita ilustrasikan sebagai berikut:

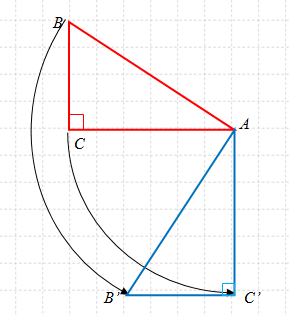
Contoh 2

Tentukan bayangan titik A(5, -10) oleh rotasi yang berpusat di titik O(0, 0) sejauh π2 $\frac{\pi }{2}$ dan arah rotasi searah putaran jarum jam.

Penyelesaian:

Oleh karena arah rotasi searah putaran jarum jam, maka besar sudut rotasi bernilai negatif.

Selanjutnya jika kita misalkan bayangan titik A(x, y) adalah A(x', y'), maka kita peroleh persamaan matriks sebagai berikut:

(x′y′ )===(cos(−π2)sin(−π2)−sin(−π2)cos(−π2) )(5−10 )(0−110 )(5−10 )(−10−5 )  $\begin{array}{lll}\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)& =& \left(\begin{array}{cc}\cos (-\frac{\pi }{2})& -\sin (-\frac{\pi }{2})\\ \sin (-\frac{\pi }{2})& \cos (-\frac{\pi }{2})\end{array}\right)\left(\begin{array}{c}5\\ -10\end{array}\right)\\ & =& \left(\begin{array}{cc}0& 1\\ -1& 0\end{array}\right)\left(\begin{array}{c}5\\ -10\end{array}\right)\\ & =& \left(\begin{array}{c}-10\\ -5\end{array}\right)\end{array}$

Dengan demikian, titik A(5, -10) oleh rotasi yang berpusat di titik O(0, 0) sejauh π2 $\frac{\pi }{2}$ dan arah rotasi searah putaran jarum jam A’(-10, -5).

Contoh 3

Tentukan bayangan garis y = 2x + 8 oleh rotasi yang berpusat di titik O(0, 0) sejauh π$\pi$dengan arah rotasi berlawanan arah dengan putaran jarum jam.

Penyelesaian:

Oleh karena arah rotasi berlawanan arah dengan putaran jarum jam, maka besar sudut rotasi bernilai psotif.

Selanjutnya jika kita misalkan bayangan titik A(x, y) adalah A(x', y'), maka kita peroleh persamaan matriks sebagai berikut:

(x′y′ )===(cosπsinπ−sinπcosπ )(xy )(−100−1 )(xy )(−x−y )  $\begin{array}{lll}\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)& =& \left(\begin{array}{cc}\cos \pi & -\sin \pi \\ \sin \pi & \cos \pi \end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)\\ & =& \left(\begin{array}{cc}-1& 0\\ 0& -1\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)\\ & =& \left(\begin{array}{c}-x\\ -y\end{array}\right)\end{array}$

Berdasarkan uraian di atas, x = -x’ dan y = -y’.

Dengan demikian, jika kita subtitusikan hasil tersebut ke persamaan garis y = 2x + 8, maka kita peroleh persamaan bayangan sebagai berikut:

y=2x+8⇔−y′=2(−x′)+8⇔y′=2x′−8  $\begin{array}{rl}& y=2x+8\\ & \iff -y^{\prime }=2(-x^{\prime })+8\\ & \iff y^{\prime }=2x^{\prime }-8\end{array}$

Jadi, bayangan garis y = 2x + 8 oleh rotasi yang berpusat di titik O(0, 0) sejauh π$\pi$ dengan arah rotasi berlawanan arah dengan putaran jarum jam adalah y = 2x - 8.

Nah, kalian sudah selesai memperlajari topik ini. Yuk kerjakan latihan soal yang ada dalam topik ini.