Rotasi Sejauh Sudut Tertentu terhadap Pusat P(a, b)

Rotasi Sejauh Sudut Tertentu terhadap Pusat P(a, b) - Pada topik sebelumnya kalian telah belajar mengenai rotasi sejauh sudut tertentu terhadap pusat 

O(0,0)$O(0,0)$. Nah, dalam topik kali ini, pusat rotasi yang akan kalian pelajari adalah P(a,b)$P(a,b)$.

Konsep Dasar

Seperti yang telah kalian pelajari, suatu rotasi ditentukan oleh pusat rotasi, besar sudut rotasi, dan arah rotasi. Adapun arah rotasi ada dua macam, yaitu berlawanan arah dengan arah putar jarum jam (sudut putar bernilai positif) dan searah dengan arah putar jarum jam(sudut putar bernilai negatif).

Bagaimanakah hasil rotasi jika titik pusat rotasi bukanlah O(0, 0), melainkan (a, b)?

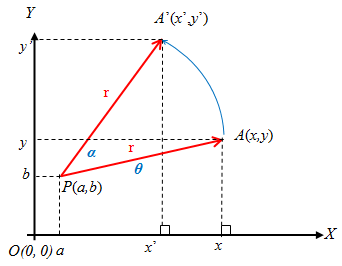
Mari kita temukan jawabannya dengan memperhatikan ilustrasi berikut.

Pada ilustrasi di atas, bayangan titik A(x,y)$A(x,y)$ dirotasikan sejauh α$\alpha$ dengan titik pusat rotasi P(a,b)$P(a,b)$ sejauh α$\alpha$ dengan arah rotasi berlawanan dengan arah putar jarum jam adalah titik A′(x′,y′)$A^{\prime }(x^{\prime },y^{\prime })$.

Jika kita gunakan perbandingan trigonometri, maka kita peroleh hasil sebagai berikut:

• x′−a=(x−a)cosα−(y−b)sinα$x^{\prime }-a=(x-a)\cos \alpha -(y-b)\sin \alpha$
• y′−b=(x−a)sinα+(y−b)cosα$y^{\prime }-b=(x-a)\sin \alpha +(y-b)\cos \alpha$

Dengan demikian, kita peroleh persamaan matriks berikut:

(x′−ay′−b )=(cosαsinα−sinαcosα )(x−ay−b )⇔(x′y′ )=(cosαsinα−sinαcosα )(x−ay−b )+(ab ) $\begin{array}{rl}& \left(\begin{array}{c}{x}^{\prime }-a\\ y^{\prime }-b\end{array}\right)=\left(\begin{array}{cc}\cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{array}\right)\left(\begin{array}{c}x-a\\ y-b\end{array}\right)\\ & \iff \left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{cc}\cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{array}\right)\left(\begin{array}{c}x-a\\ y-b\end{array}\right)+\left(\begin{array}{c}a\\ b\end{array}\right)\end{array}$

Nah, apakah kalian sudah paham dengan materi di atas?

Mari kita cermati beberapa contoh berikut agar kalian semakin paham.

Contoh 1

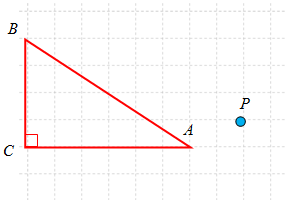
Tentukan bayangan ∆ABC$∆ABC$ terhadap rotasi yang berpusat di titik P$P$ sejauh π2$\frac{\pi }{2}$ radian dan arah rotasi berlawanan arah dengan arah putar jarum jam.

Penyelesaian:

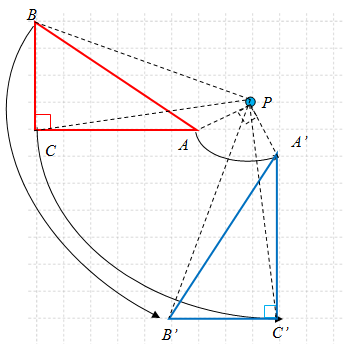
Hasil rotasi ketiga titik sudut dari ∆ABC$∆ABC$ dapat kita ilustrasikan sebagai berikut:

Pada ilustrasi di atas, tampak bahwa bayangan ∆ABC$∆ABC$ adalah ∆A′B′C′$∆A^{\prime }{B}^{\prime }{C}^{\prime }$.

Ingat, rotasi tidak mengubah bentuk benda.

Contoh 2

Tentukan bayangan titik A(6,8)$A(6,8)$ oleh rotasi sejauh π2$\frac{\pi }{2}$ dengan titik pusat rotasi P(2,3)$P(2,3)$dan arah rotasi berlawanan arah dengan arah putar jarum jam.

Penyelesaian:

Oleh karena arah rotasi berlawanan arah dengan arah putar jarum jam, maka besar sudut rotasi bernilai positif.

Selanjutnya jika kita misalkan bayangan titik A(x,y)$A(x,y)$ adalah A′(x′,y′)$A^{\prime }(x^{\prime },y^{\prime })$, maka kita peroleh persamaan matriks sebagai berikut:

(x′y′ )====(cosπ2sinπ2−sinπ2cosπ2 )(6−28−3 )+(23 )(01−10 )(45 )+(23 )(−54 )+(23 )(−37 )$\begin{array}{lll}\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)& =& \left(\begin{array}{cc}\cos \frac{\pi }{2}& -\sin \frac{\pi }{2}\\ \sin \frac{\pi }{2}& \cos \frac{\pi }{2}\end{array}\right)\left(\begin{array}{c}6-2\\ 8-3\end{array}\right)+\left(\begin{array}{c}2\\ 3\end{array}\right)\\ & =& \left(\begin{array}{cc}0& -1\\ 1& 0\end{array}\right)\left(\begin{array}{c}4\\ 5\end{array}\right)+\left(\begin{array}{c}2\\ 3\end{array}\right)\\ & =& \left(\begin{array}{c}-5\\ 4\end{array}\right)+\left(\begin{array}{c}2\\ 3\end{array}\right)\\ & =& \left(\begin{array}{c}-3\\ 7\end{array}\right)\end{array}$

Dengan demikian, bayangan titik A(6,8)$A(6,8)$ oleh rotasi sejauh π2$\frac{\pi }{2}$ dengan titik pusat rotasi P(2,3)$P(2,3)$ dan arah rotasi berlawanan arah dengan arah putar jarum jam adalah titik A′(−3,7)$A^{\prime }(-3,7)$.

Contoh 1 dan 2 di atas berkaitan dengan hasil rotasi suatu titik. Nah, pada contoh 3 berikut ini berkaitan dengan hasil rotasi sebuah garis.

Contoh 3

Tentukan bayangan garis y=3x+1$y=3x+1$ oleh rotasi sejauh π$\pi$ dengan titik pusat rotasi P(4,5)$P(4,5)$ dan arah rotasi berlawanan arah dengan arah putar jarum jam.

Penyelesaian:

Oleh karena arah rotasi berlawanan arah dengan arah putar jarum jam, maka besar sudut rotasi bernilai positif.

Selanjutnya jika kita misalkan bayangan titik (x,y)$(x,y)$ adalah (x′,y′)$(x^{\prime },y^{\prime })$, maka kita peroleh persamaan matriks sebagai berikut:

(x′y′ )====(cosπsinπ−sinπcosπ )(x−4y−5 )+(45 )(−100−1 )(x−4y−5 )+(45 )(−x+4−y+5 )+(45 )(−x+8−y+10 ) $\begin{array}{lll}\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)& =& \left(\begin{array}{cc}\cos \pi & -\sin \pi \\ \sin \pi & \cos \pi \end{array}\right)\left(\begin{array}{c}x-4\\ y-5\end{array}\right)+\left(\begin{array}{c}4\\ 5\end{array}\right)\\ & =& \left(\begin{array}{cc}-1& 0\\ 0& -1\end{array}\right)\left(\begin{array}{c}x-4\\ y-5\end{array}\right)+\left(\begin{array}{c}4\\ 5\end{array}\right)\\ & =& \left(\begin{array}{c}-x+4\\ -y+5\end{array}\right)+\left(\begin{array}{c}4\\ 5\end{array}\right)\\ & =& \left(\begin{array}{c}-x+8\\ -y+10\end{array}\right)\end{array}$

Berdasarkan uraian di atas, x=−x′+8$x=-x^{\prime }+8$ dan y=−y′+10$y=-y^{\prime }+10$.

Dengan demikian, jika kita subtitusikan hasil tersebut ke persamaan garis y=3x+1$y=3x+1$, maka kita peroleh persamaan bayangan sebagai berikut:

y=3x+1⇔−y′+10=3(−x′+8)+1⇔−y′+10=−3x′+25⇔−y′=−3x′+15⇔y′=3x′−15 $\begin{array}{rl}& y=3x+1\\ & \iff -y^{\prime }+10=3(-x^{\prime }+8)+1\\ & \iff -y^{\prime }+10=-3x^{\prime }+25\\ & \iff -y^{\prime }=-3x^{\prime }+15\\ & \iff y^{\prime }=3x^{\prime }-15\end{array}$

Jadi, bayangan garis y=3x+1$y=3x+1$ oleh rotasi sejauh π$\pi$ dengan titik pusat rotasi P(4,5)$P(4,5)$dan arah rotasi berlawanan arah dengan arah putar jarum jam adalah y=3x−15$y=3x-15$.

Nah, sekarang saatnya kalian menguji pemahaman kalian tentang materi di atas, yaitu dengan mengerjakan sepuluh latihan soal dalam topik ini.