Masalah nyata yang berkaitan dengan turunan fungsi trigonometri

Masalah nyata yang berkaitan dengan turunan fungsi trigonometri - Pada topik sebelumnya kalian telah belajar tentang konsep turunan fungsi aljabar dan fungsi trigonometri. Kalian juga telah belajar menerapkan konsep turunan fungsi aljabar untuk masalah nyata maupun masalah matematika.

Apakah kalian masih ingat terapan konsep turunan digunakan untuk apa?

Penerapan konsep turunan antara lain dipakai untuk :
1) menentukan persamaan garis singgung kurva
2) menentukan interval dimana fungsi naik dan interval dimana fungsi turun
3) menentukan menyelesaikan masalah-masalah ekstrim
4) menentukan gerak rektilinear (kecepatan dan percepatan pada gerak lurus)
5) perhitungan pada limit fungsi

Nah, pada topik kali ini, kalian akan belajar menyelesaikan masalah-masalah nyata yang berkaitan dengan turunan fungsi trigonometri.

Dalam hal ini, tentu kalian harus ingat turunan fungsi trigonometri, antara lain :

1. turunan fungsi y = sin x adalah y’ = cos x
2. turunan fungsi y = cos x adalah y’ = - sin x
3. turunan fungsi y = tan x adalah y’ = sec2 x, dan seterusnya.

Agar lebih jelas mari kita perhatikan contoh berikut ini.

Contoh :

Sebuah tangga panjangnya 8 meter bersandar pada dinding tegak yang tingginya 6 meter dengan bagian atas tangga melewati dinding. Jika ujung bawahnya ditarik horizontal dengan kecepatan 2 meter/detik menjauhi dinding, tentukan kecepatan vertikal ujung atas tangga pada saat tangga membentuk sudut 60o dengan permukaan lantai.

Penyelesaian :

Perhatikan gambar berikut :

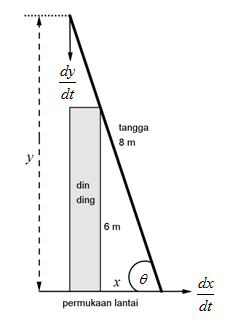
Misalkan pada saat t, sudut antara tangga dengan permukaan lantai adalah ϴ, jarak ujung bawah tangga ke dinding adalah x meter, dan jarak ujung atas tangga ke permukaan lantai adalah y meter.

Oleh karena kecepatan vertikal ujung atas tangga ditanyakan, maka kita perlu menentukan dy/dt pada saat tangga membentuk sudut 60o dengan permukaan lantai dan dx/dt = 2 m/det.

Berdasarkan gambar di atas,

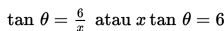
Turunan implisit terhadap t dari kedua ruas menghasilkan

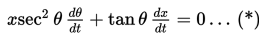
Untuk ϴ = 60o berlaku :

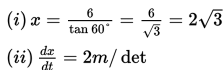
Jika hasil di atas disubtitusikan ke persamaan (*), maka diperoleh hasil sebagai berikut :

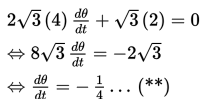
Jika kita melihat gambar di atas lagi, maka diperoleh

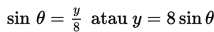
Turunan implisit terhadap t dari kedua ruas menghasilkan

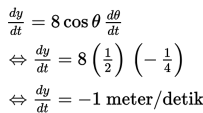
(tanda negatif menunjukkan arah ke bawah)

Dengan demikian, kecepatan vertikal ujung atas tangga adalah -1 m/det .