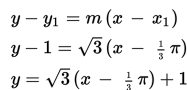Setelah kalian paham cara menurunkan fungsi trigonometri, sekarang kita akan menerapkannya untuk menentukan titik-titik stasioner (titik maximum, titik minimum dan titik belok), menentukan interval fungsi naik dan fungsi turun serta menentukan persamaan garis singgung dari fungsi trigonometri.
Agar lebih jelas, mari kita cermati beberapa contoh berikut ini.
Contoh 1 :
Tentukan titik stasioner dan jenisnya dari fungsi : f(x) = sin x + cos x, untuk 0o ≤ x ≤ 360o
Penyelesaian :
Kita ingat pada fungsi aljabar bahwa titik stasioner dicapai jika turunannya adalah nol, demikian juga untuk fungsi trigonometri, titik stasioner dicapai juga jika turunannya sama dengan nol.

Jadi titik stasioner untuk fungsi di atas adalah
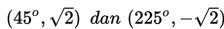
Untuk menentukan jenis titik stasioner, kita gunakan pertolongan garis bilangan :
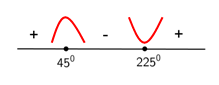
Jadi jenis titik (45o, √2) adalah titik balik maksimum dan titik (225o, -√2) adalah titik balik minimum.
Contoh 2 :
Tentukan interval fungsi naik dan fungsi turun dari fungsi f(x) = √3 cos x – sin x, untuk 0 ≤ x ≤ 2π
Penyelesaian :
Seperti pada fungsi aljabar, bahwa fungsi akan naik jika f’(x) > 0 dan fungsi akan turun jika f’(x) < 0.

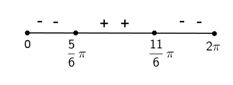
Jadi fungsi naik untuk interval 5/6 π < x < 11/6 π
Syarat fungsi turun => f’(x) < 0
Jadi fungsi turun untuk interval 0 < x < 5/6 π atau 11/6 π < x < 2π.
Jadi fungsi turun untuk interval 0 < x < 5/6 π atau 11/6 π < x < 2π.
Contoh 3 :
Tentukan persamaan garis singgung kurva y = √3 sin x – cos x di titik (1/3 π,1).
Penyelesaian :
Sebelum menentukan persamaan garis singgung suatu kurva kita cari dulu gradien dari fungsi tersebut dengan cara menentukan turunan fungsinya.
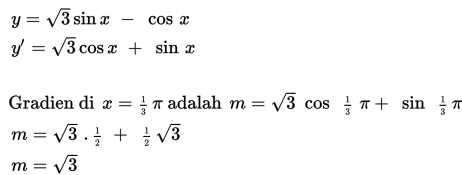
Jadi persamaan garis singgung di titik (1/3 π,1) adalah :