Refleksi terhadap Dua Sumbu yang Sejajar dengan Sumbu X - Dalam topik sebelumnya, kalian telah belajar mengenai refleksi terhadap garis
Seperti yang telah kalian ketahui, bayangan titik oleh refleksi terhadap garis adalah titik .
Nah, dari uraian di atas, dapat kita simpulkan bahwa bayangan titik oleh refleksi terhadap garis dilanjutkan dengan refleksi garis adalah titik .
Berikut ini adalah salah satu ilustrasi mengenai kedudukan titik bayangan dari transformasi di atas.
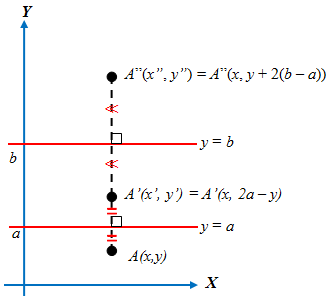
Tahukah kalian bagaimana bentuk persamaan matriks dari transformasi tersebut?
Materi di atas mudah dipahami bukan?
Penyelesaian:
Geometri Analitik
Persamaan Matriks
Nah, bagaimanakah cara menentukan bayangan suatu garis oleh refleksi berurutan terhadap dua garis yang sejajar dengan sumbu ?
Penyelesaian:
Yuk kita selesaikan soal di atas.
Oleh karena bayangan titik oleh transformasi dalam soal adalah , maka kita peroleh hubungan sebagai berikut:
Nah, jika kita subtitusikan dan ke persamaan garis , maka akan kita peroleh persamaan garis bayangan sebagai berikut:
Jadi, bayangan garis oleh refleksi terhadap garis dilanjutkan dengan refleksi terhadap garis adalah .
Nah, kalian telah selesai belajar mengenai materi di atas.
Yuk kerjakan latihan soal dalam topik ini.
. Nah, dalam topik ini kalian akan belajar mengenai komposisi transformasi refleksi terhadap garis yang dilanjutkan dengan refleksi terhadap garis .
Seperti yang telah kalian ketahui, bayangan titik oleh refleksi terhadap garis adalah titik .
Dengan demikian,
- bayangan titik oleh refleksi terhadap garis adalah titik
- bayangan titik oleh refleksi terhadap garis adalah titik
Nah, dari uraian di atas, dapat kita simpulkan bahwa bayangan titik oleh refleksi terhadap garis dilanjutkan dengan refleksi garis adalah titik .
Berikut ini adalah salah satu ilustrasi mengenai kedudukan titik bayangan dari transformasi di atas.
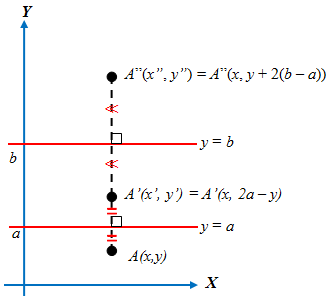
Tahukah kalian bagaimana bentuk persamaan matriks dari transformasi tersebut?
Ya, oleh karena koordinat titik bayangan adalah , maka bentuk persamaan matriksnya adalah sebagai berikut:
Materi di atas mudah dipahami bukan?
Agar kalian semakin paham dengan materi di atas, yuk kita cermati beberapa contoh soal berikut.
Contoh 1
Tentukan bayangan titik oleh refleksi terhadap garis dilanjutkan dengan refleksi terhadap garis .
Penyelesaian:
Soal di atas dapat diselesaikan dengan dua cara, yaitu penyelesaian dengan geometri analitik dan penyelesaian dengan menggunakan persamaan matriks.
Geometri Analitik
Oleh karena refleksi pertama adalah terhadap garis , maka .
Selanjutnya, karena refleksi kedua adalah terhadap garis , maka .
Nah, karena bayangan titik oleh refleksi terhadap garis dilanjutkan dengan refleksi garis adalah titik , maka bayangan titik terhadap transformasi dalam soal adalah titik .
Persamaan Matriks
Jika dimisalkan bayangan titik terhadap transformasi dalam soal adalah , maka
Berdasarkan uraian di atas, dapat disimpulkan bahwa bayangan titik adalah titik .
Nah, bagaimanakah cara menentukan bayangan suatu garis oleh refleksi berurutan terhadap dua garis yang sejajar dengan sumbu ?
Yuk kita temukan jawabannya dengan mencermati conoth soal berikut.
Contoh 2
Tentukan bayangan garis oleh refleksi terhadap garis dilanjutkan dengan refleksi terhadap garis .
Penyelesaian:
Soal di atas dapat diselesaikan dalam tiga langkah, yaitu
- Memisalkan bayangan titik adalah titik .
- Menentukan hubungan antara variabel dan , serta hubungan antara variabel dan .
- Mensubtitusikan variabel dan ke persamaan garis.
Yuk kita selesaikan soal di atas.
Oleh karena bayangan titik oleh transformasi dalam soal adalah , maka kita peroleh hubungan sebagai berikut:
Nah, jika kita subtitusikan dan ke persamaan garis , maka akan kita peroleh persamaan garis bayangan sebagai berikut:
Jadi, bayangan garis oleh refleksi terhadap garis dilanjutkan dengan refleksi terhadap garis adalah .
Nah, kalian telah selesai belajar mengenai materi di atas.
Yuk kerjakan latihan soal dalam topik ini.