Uji Hipotesis Dua Pihak - Hipotesis adalah asumsi atau dugaan mengenai sesuatu hal. Hipotesis bisa benar ataupun tidak benar. Untuk menentukan apakah hipotesis itu benar atau tidak benar, dapat ditempuh dengan melakukan pengujian hipotesis.
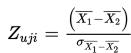

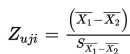


Mari kita mencermati beberapa contoh soal berikut ini.
Contoh 1 :
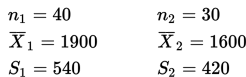
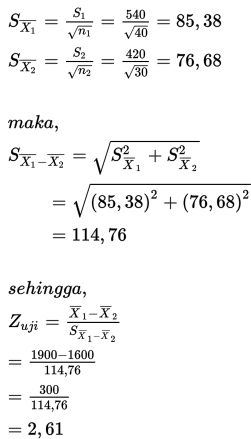
Tabel Distribusi Normal Standar (Tabel Z)
Contoh 2 :

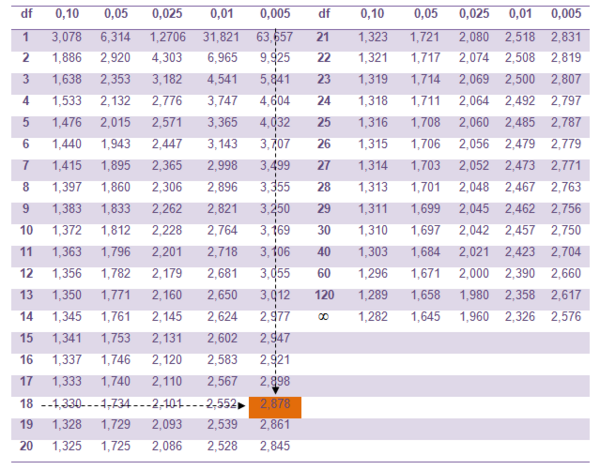
Tabel Distribusi t-student
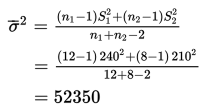
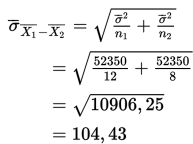
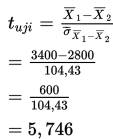
Contoh 3 :
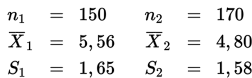
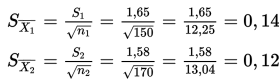
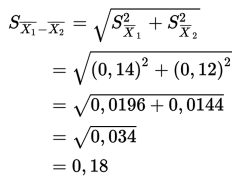
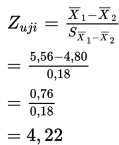
Uji hipotesis beda dua mean populasi dengan distribusi normal
Langkah-langkah pengujian hipotesis adalah sebagai berikut :
1. Penentuan H0 dan H1
- H0 : μ1 - μ2 = 0 atau μ1 = μ2
- H1 : μ1 - μ2 ≠ 0 atau μ1 ≠ μ2
2. Penentuan Zkritis
3. Penentuan Zuji
3. Penentuan Zuji
- Kemungkinan pertama (yang diketahui adalah σ1 dan σ2)
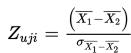
dengan

- Kemungkinan kedua (yang diketahui adalah S1 dan S2)
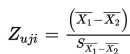
dengan

4. Pengambilan keputusan
Terima H0 jika
- Zkritis bawah ≤ Zuji ≤ Zkritis atas
Tolak H0 jika :
- Zuji < Zkritis bawah
- Zuji > Zkritis atas
Uji hipotesis beda dua mean populasi dengan distribusi t-student
Distribusi t untuk uji hipotesis beda dua mean digunakan jika kondisi yang dihadapi adalah sebagai berikut:
- Standar deviasi populasi σ tidak diketahui (yang diketahui adalah s)
- Sampelnya kecil (n < 30)
- Populasinya dianggap berdistribusi normal
- Standar deviasi dari dua populasi yang tidak diketahui besarnya tersebut adalah sama besarnya (σ1 = σ2)
Hal-hal penting dalam pengujian beda dua mean dengan distribusi t:
- Penentuan nilai tkritis tergantung dari derajat keyakinan dan derajat bebas. Dalam hal ini derajat bebasnya adalah n1 + n2 – 2
- Penentuan tuji diperoleh dari rumus :

Mari kita mencermati beberapa contoh soal berikut ini.
Contoh 1 :
Terdapat dugaan bahwa mean pendapatan rumah-tangga bulanan dari kota A dan kota B adalah sama. Seseorang ingin menguji hipotesis tersebut dengan mengumpulkan data sebagai berikut. Dari kota A diambil 40 anggota keluargasebagai sampel, dan didapat mean pendapatan bulanannya $1,900 dengan standar deviasi $540. Dari kota B diambil 30 anggota keluarga sebagai sampel, dan didapat mean pendapatan bulanannya $1.600 dengan standar deviasi $420.
Bantulah orang tersebut dalam melakukan uji hipotesisnya dengan menggunakan derajat keyakinan 95% !
Penyelesaian :
Diketahui :
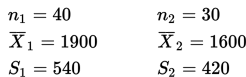
1. Penentuan H0 dan H1
H0 : μ1 = μ2 (mean pendapatan rumah tangga bulanan dari kota A dan kota B
adalah sama)
H1 : μ1 ≠ μ2
adalah sama)
H1 : μ1 ≠ μ2
2. Penentuan nilai kritis
dk = 95% = 0,95
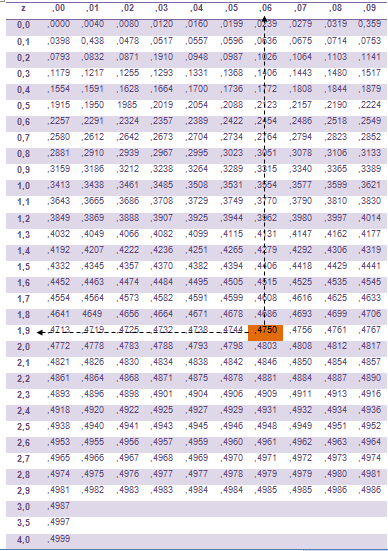
Karena uji 2 pihak maka yang kita gunakan hanyalah ½ dk = ½ (0,95) = 0,475 , sehingga Zkritis = ±1,96 (lihat tabel Z)
3. Penentuan nilai uji
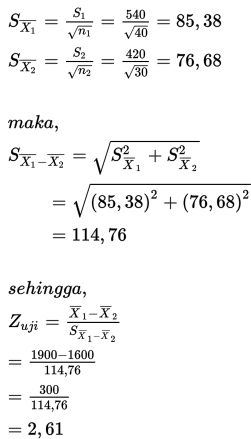
4. Karena 2,61 > + 1,96 maka kita menolak H0.
Kesimpulannya, pernyataan bahwa mean pendapatan dua kota tersebut sama adalah tidak benar.
Kesimpulannya, pernyataan bahwa mean pendapatan dua kota tersebut sama adalah tidak benar.
Tabel Distribusi Normal Standar (Tabel Z)

Contoh 2 :
Diduga bahwa tidak ada beda antara mean daya tahan hidup dua merk batu baterai, yaitu merk A dan B. Untuk menguji hipotesis tersebut telah dikumpulkan data sebagai berikut: n1 = 12, X1= 3.400 jam, S1 = 240 jam, n2 = 8, X2= 2.800 jam, S2 = 210 jam. Bagaimana hasil ujinya? Gunakan derajat keyakinan 99%.
Penyelesaian :
1. Penentuan H0 dan H1
- H0 : μ1 = μ2 (tidak ada beda antara mean daya tahan hidup dua merk batu baterai)
- H1 : μ1 ≠ μ2
2. Penentuan nilai kritis

Tabel Distribusi t-student

3. Penentuan nilai uji
Dugaan atas variansi populasi gabungan 2 populasi :
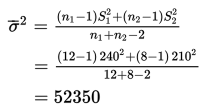
Standar deviasi sampling :
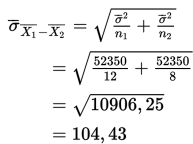
sehingga
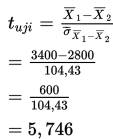
4. Karena 5,746> + 2,878 maka kita menolak H0.
Kesimpulannya, pernyataan bahwa tidak ada beda antara mean daya tahan hidup dua merk baterai adalah tidak benar.
Contoh 3 :
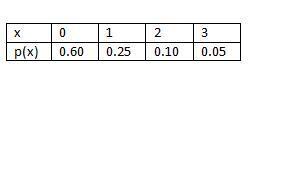
Informasi-informasi berikut ini diperoleh dari dua sampel independen dari dua buah populasi.
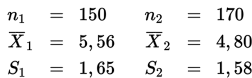
Dengan informasi tersebut, ujilah hipotesis bahwa dua mean populasi adalah berbeda. Gunakan tingkat signifikansi 5%.
Penyelesaian :
1. Penentuan H0 dan H1
- H0 : μ1 = μ2 (dua mean populasi adalah berbeda)
- H1 : μ1 ≠ μ2
2. Penentuan nilai kritis
- α = 0,05 maka Zkritis = ± 1,96
3. Penentuan nilai uji
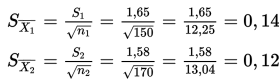
maka
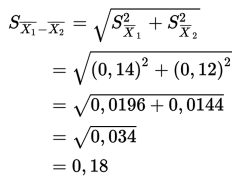
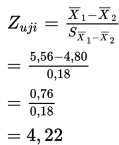
4. Karena 4,22 > + 1,96 maka kita menolak H0.
Kesimpulannya, pernyataan bahwa mean dua populasi berbeda adalah tidak benar.