Volume Benda yang Mengelilingi Sumbu X

Volume Benda yang Mengelilingi Sumbu X - Pada topik sebelumnya, kalian telah menggunakan integral tertentu untuk menghitung luas daerah. Hal ini tidak mengherankan karena integral tertentu memang diciptakan untuk keperluan itu. Selain untuk menghitung luas daerah, ternyata integral tertentu dapat juga digunakan untuk memecahkan persoalan lainnya. Salah satunya volume benda putar.

        Jika sebuah bidang datar diputar mengelilingi suatu sumbu yang berupa garis, maka akan terbentuk sebuah ruang yang merupakan lintasan bidang datar tersebut. Volume dari ruang tersebut dinamakan volume benda putar. Misalkan, jika sebuah bidang datar yang berbentuk lingkaran diputar sebesar 360° mengelilingi diamaternya, maka akan terbentuk sebuah ruang yang berbentuk bola. Jika sebuah bidang datar berbentuk segitiga siku-siku diputar sebesar 360° mengelilingi salah satu sisi siku-sikunya sebagai sumbu putar, maka akan terbentuk sebuah bangun ruang yang berbentuk kerucut.

              

        Hampir tiap besaran yang dapat dianggap sebagai hasil pemotongan sesuatu menjadi bagian-bagian yang lebih kecil, aproksimasi tiap bagian, penjumlahan, dan pengambilan limit apabila tiap bagian mengecil, dapat diartikan sebagai suatu integral. Prinsip inilah yang akan digunakan untuk menurunkan rumus volume benda putar. Untuk topik kali ini, kalian akan belajar menentukan volume benda putar mengelilingi sumbu X. Bagaimana caranya? Mari kita pelajari bersama.

📖 KONSEP

Perhatikan gambar berikut.

                            

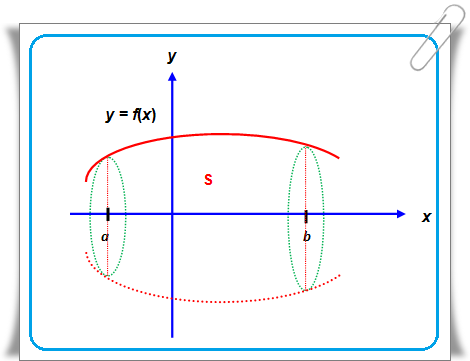
        Misalkan daerah S dibatasi oleh kurva y = f(x), sumbu X, garis x = a, garis x = b, dengan a < b diputar mengelilingi sumbu X sebesar 360°. Untuk mendapatkan volume benda putar tersebut, dibuatlah potongan tabung-tabung kecil sebagai pendekatan volume benda. Jika jari-jari potongan tabung kecil itu y dan tingginya δx, maka:

                                                               δV=πy2δx$\delta V=\pi y^2\delta x$

Volume benda putar tersebut merupakan jumlah potongan tabung-tabung itu, sehingga:

                                                               V=∑i=1nπyi2δxi$V=\sum _{i=1}^n\pi {y_i}^2\delta x_i$

dengan n jumlah potongan tabung.

Untuk δx yang cukup kecil, akan dihasilkan pendekatan volume yang sempurna, yaitu:

                                                               V=limδx→0$V=\underset{\delta x\to 0}{lim}$ ∑i=1nπyi2δxi$\sum _{i=1}^n\pi {y_i}^2\delta x_i$

Bentuk limit di atas dapat dinyatakan dalam bentuk integral:

                                                               V=π∫aby2dx$V=\pi \underset{a}{\overset{b}{\int }}{y}^{2}dx$

Oleh karena y = f(x), maka bentuk tersebut dapat pula ditulis sebagai:

                                                               V=π∫ab(f(x))2dx$V=\pi \underset{a}{\overset{b}{\int }}{(f(x))}^{2}dx$

                

Contoh

Ayo, tentukan volume benda putar yang terjadi jika daerah yang dibatasi oleh garis y = 2x, sumbu X, dan garis x = 2 diputar 360° mengelilingi sumbu X.

Jawab:

Daerah tersebut adalah sebagai berikut.

                                          

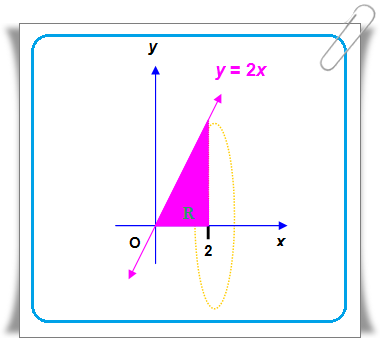
Batas-batas pengintegralannya adalah x = 0 sampai x = 2.

Volumenya adalah sebagai berikut.

V=π∫02(2x)2dx=π∫024x2dx=43π[x3]20=43π(23−03)=

323π$\mathrm{<br>}$

$V=\pi \underset{0}{\overset{2}{\int }}{(2x)}^{2}dx=\pi \underset{0}{\overset{2}{\int }}4x^{2}dx=\frac{4}{3}\pi {\left[x^3\right]}_0^2=\frac{4}{3}\pi \left(2^3-0^3\right)=\frac{32}{3}\pi$

Jadi, volume benda putar tersebut adalah 323π$\frac{32}{3}\pi$ satuan volume.

Pada uraian di atas, kalian sudah belajar cara menentukan volume benda putar yang mengelilingi sumbu X. Agar pemahaman kalian lebih mendalam, sekarang coba kerjakan soal-soal berikut.