Volume Benda yang Mengelilingi Sumbu Y

Volume Benda yang Mengelilingi Sumbu Y - Ketika di sekolah dasar, kalian telah dapat menentukan volume bola dari volume kerucut dengan melakukan percobaan, kemudian kalian dapat menemukan rumusnya.

              

        Bola dan kerucut merupakan bangun ruang. Tahukah kalian bahwa bola dapat diperoleh dari sebuah lingkaran yang diputar terhadap diameternya? Bagaimana dengan kerucut? Ternyata kerucut dapat diperoleh dari sebuah segitiga siku-siku yang diputar terhadap salah satu sisi tegaknya. Kita dapat menganggap diameter lingkaran dan sisi tegak segitiga siku-siku sebagai sumbu putarnya sehingga dapat dikatakan bahwa bola dan kerucut sebagai benda putar. Pada topik berikut ini, kalian akan mempelajari cara menentukan volume benda putar mengelilingi sumbu Y. Agar kalian dapat memahaminya, simak dengan saksama ya.

📖 KONSEP

Pada topik sebelumnya, kalian telah mempelajari cara menentukan volume benda putar mengelilingi sumbu X. Tahukah kalian bahwa kita tidak hanya dapat menentukan volume benda putar dari sebuah bidang yang mengelilingi sumbu X saja, kita pun dapat juga menentukan volume benda putar dari sebuah bidang jika diputar mengelilingi sumbu Y.

Perhatikan gambar berikut.

                            

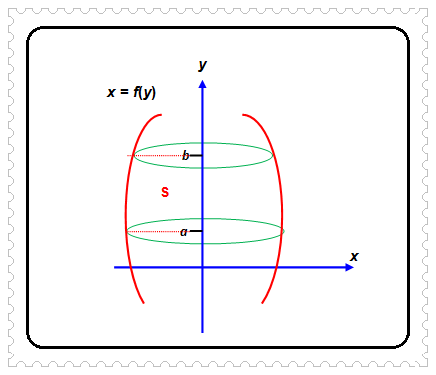
        Misalkan daerah S dibatasi oleh kurva x = f(y), sumbu Y, garis y = a, garis y = b, dengan a < b diputar mengelilingi sumbu Y sebesar 360°. Dengan cara yang sama seperti saat menentukan volume benda putar dari sebuah bidang jika diputar mengelilingi sumbu X, kita dapatkan rumus untuk δV, yaitu:

                                                               δV=∑i=1nπxi2δyi$\delta V=\sum _{i=1}^n\pi {x_i}^2\delta y_i$

dengan n jumlah potongan tabung.

Untuk δy yang cukup kecil, akan dihasilkan pendekatan volume yang sempurna, yaitu:

                                                               V=limδy→0$V=\underset{\delta y\to 0}{lim}$ ∑i=1nπxi2δyi$\sum _{i=1}^n\pi {x_i}^2\delta y_i$

Bentuk limit di atas dapat dinyatakan dalam bentuk integral menjadi:

                                                               V=π∫abx2dy$V=\pi \underset{a}{\overset{b}{\int }}{x}^{2}dy$

Oleh karena x = f(y), maka bentuk tersebut dapat pula ditulis sebagai:

                                                               V=π∫ab(f(y))2dy$V=\pi \underset{a}{\overset{b}{\int }}{(f(y))}^{2}dy$

                

🍇 Contoh

☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳

Ayo, tentukan volume benda putar yang terjadi jika daerah yang dibatasi oleh kurva f(x) = x2 – 3, sumbu X, dan sumbu Y diputar 360° mengelilingi sumbu Y.

Jawab:

Untuk menentukan volume benda putar tersebut, terlebih dahulu kalian harus menentukan batas-batas pengintegralan, yaitu ordinat titik potong kurva f(x) = x2 – 3 dengan sumbu Y dan dengan sumbu X.

                                          

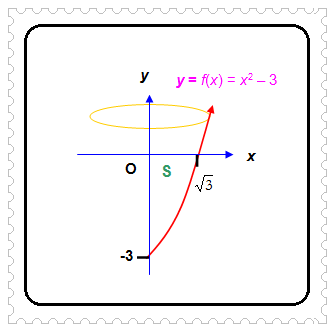
Ordinat titik potong kurva f(x) = x2 – 3 dengan sumbu Y didapat dengan mensubstitusikan x = 0 ke 
y = x2 – 3.

y = 02 – 3 = -3

Jadi, ordinat titik potong kurva f(x) = x2 – 3 dengan sumbu Y adalah y = -3.

Sementara ordinat titik potong kurva f(x) = x2 – 3 dengan sumbu X adalah y = 0.

Dengan demikian, batas pengintegralannya adalah y = -3 sampai y = 0.

Setelah mendapatkan batas-batas pengintegralan, sekarang coba nyatakan persamaan kurva y = f(x) = x2 – 3 menjadi persaamaan x2 dalam peubah y.

y = x2 – 3 ⇒ x2 = y + 3.

Volume benda putar tersebut adalah sebagai berikut.

V=π∫abx2dy=π∫−30(y+3)dy=π[12y2+3y]0−3=π(0−(12(−3)2+3(−3)))=412π$\begin{array}{l}\mathrm{<br>}\end{array}$

$\begin{array}{ll}V& =\pi \underset{a}{\overset{b}{\int }}{x}^{2}dy\\ & =\pi \underset{-3}{\overset{0}{\int }}(y+3)dy\\ & =\pi {\left[\frac{1}{2}{y}^2+3y\right]}_{-3}^0\\ & =\pi \end{array}$

$\begin{array}{l}\left(0-\left(\frac{1}{2}{(-3)}^2+3(-3)\right)\right)\\ & =4\frac{1}{2}\pi \end{array}$

Jadi, volume benda putar tersebut adalah 412π$4\frac{1}{2}\pi$ satuan volume.

☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳

        Pada uraian di atas, kalian sudah belajar cara menentukan volume benda putar yang mengelilingi sumbu Y. Agar pemahaman kalian lebih mendalam, sekarang coba kerjakan soal-soal berikut.