Menghitung Panjang Kurva (Panjang Busur)

Menghitung Panjang Kurva (Panjang Busur) - Ketika kalian duduk di bangku sekolah dasar, kalian mungkin pernah diminta untuk mengukur keliling suatu benda dengan bentuk tak beraturan dengan menggunakan tali atau benang.

Sebenarnya untuk mengukur keliling/panjang suatu benda dengan bentuk tak beraturan, kalian dapat menggunakan konsep integral tentu.

Bagaimanakah penggunaan konsep integral tentu dalam menentukan panjang kurva (panjang busur)?

Yuk kita temukan jawabannya dalam topik ini.

Konsep Dasar

Sebagai ilustrasi, misalkan fungsi f$f$ kontinu pada interval [a,b]$[a,b]$. Nah, kita akan mencoba menentukan panjang kurva y=f(x)$y=f(x)$ dari x=a$x=a$ sampai x=b$x=b$.

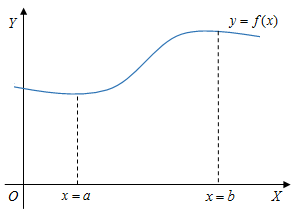
Untuk menentukan panjang kurva y=f(x)$y=f(x)$ dari x=a$x=a$ sampai x=b$x=b$, kita perlu membuat partisi yang membagi interval [a,b]$[a,b]$ menjadi n$n$ bagian dengan panjang interval sama, yaitu sebesar Δx=b−an$\mathrm{\Delta }x=\frac{b-a}{n}$.

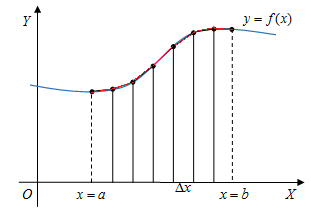
Jika setiap titik pada partisi yang berdekatan kita hubungkan dengan garis lurus, maka panjang seluruh garis lurus tersebut nilainya akan mendekati panjang kurva yang sebenarnya. Dengan kata lain, semakin banyak partisi yang kita buat, maka nilainya semakin mendekati panjang kurva yang sebenarnya.

Misalkan sk$s_k$ adalah panjang ruas garis yang menghubungkan titik (xk−1,yk−1)$\left(x_{k-1},y_{k-1}\right)$ dan (xk,yk)$(x_k,y_k)$.

Panjang ruas garis tersebut dapat ditentukan dengan rumus sebagai berikut:

sk====(xk−xk−1)2+(yk−yk−1)2‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾√(Δxk)2+(Δyk)2‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾√(1+(ΔykΔxk)2)(Δxk)2‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾√Δxk1+(ΔykΔxk)2‾‾‾‾‾‾‾‾‾‾‾√$\begin{array}{l}{\mathrm{<br>}}_{}\end{array}$

$\begin{array}{lll}{s}_k& =& \sqrt{{\left(x_k-x_{k-1}\right)}^2+{\left(y_k-y_{k-1}\right)}^2}\\ & =& \sqrt{{\left(\mathrm{\Delta }{x}_k\right)}^2+{\left(\mathrm{\Delta }{y}_k\right)}^2}\\ & =& \sqrt{\left(1+{\left(\frac{\mathrm{\Delta }{y}_k}{\mathrm{\Delta }{x}_k}\right)}^2\right){\left(\mathrm{\Delta }{x}_k\right)}^2}\\ & =& \mathrm{\Delta }{x}_k\sqrt{1+{\left(\frac{\mathrm{\Delta }{y}_k}{\mathrm{\Delta }{x}_k}\right)}^2}\\ & & \end{array}$

Pada uraian di atas,

• Δxk=xk−xk−1$\mathrm{\Delta }{x}_k=x_k-x_{k-1}$
• Δyk=yk−yk−1$\mathrm{\Delta }{y}_k=y_k-y_{k-1}$

Selanjutnya, jika kita misalkan h=xk−xk−1$h=x_k-x_{k-1}$, maka ΔykΔxk=yk−yk−1xk−xk−1=f(xk)−f(xk−1)h=f(xk−1+h)−f(xk−1)h$\frac{\mathrm{\Delta }{y}_k}{\mathrm{\Delta }{x}_k}=\frac{y_k-y_{k-1}}{x_k-x_{k-1}}=\frac{f(x_k)-f(x_{k-1})}{}$

$\frac{h}{}=\frac{f(x_{k-1}+h)-f(x_{k-1})}{h}$.

Nah, jika banyak partisi mendekati tak hingga (n→∞$n\to \infty$), maka jarak antar partisi menjadi semakin kecil (h→0$h\to 0$).

Akibatnya, limh→0ΔykΔxk=limh→0(f(xk−1+h)−f(xk−1)h)=f′(x∗k)$\underset{h\to 0}{lim}\frac{\mathrm{\Delta }{y}_k}{\mathrm{\Delta }{x}_k}=\underset{h\to 0}{lim}(\frac{f(x_{k-1}+h)-}{}$

$\frac{f(x_{k-1})}{h})=f^{\prime }(x_k^{\ast })$, dimana x∗k$x_k^{\ast }$ terletak diantara xk$x_k$dan xk−1$x_{k-1}$.

Dengan demikian, dapat disimpulkan bahwa sk=Δxk1+(f′(x∗x))2‾‾‾‾‾‾‾‾‾‾‾‾√$s_k=\mathrm{\Delta }{x}_k\sqrt{1+{\left(f^{\prime }(x_x^{\ast })\right)}^2}$.

Selanjutnya, karena panjang seluruh ruas garis yang menghubungkan setiap titik pada partisi merupakan pendekatan dari panjang kurva yang sebenarnya, maka nilai pendekatan panjang kurva adalah s=∑k=1nΔxk1+(f′(x∗k)2)‾‾‾‾‾‾‾‾‾‾‾‾‾√$s=\sum _{k=1}^n\mathrm{\Delta }{x}_k\sqrt{1+\left(f^{\prime }{(x_k^{\ast })}^2\right)}$.

Apa yang dapat kalian simpulkan dari uraian di atas?

Ya, jika kita gunakan konsep integral tentu, maka akan kita peroleh hasil sebagai berikut:

• Jika titik A(p,r)$A(p,r)$ dan B(q,s)$B(q,s)$ terletak pada kurva y=f(x)$y=f(x)$ dan f′(x)$f^{\prime }(x)$ kontinu pada interval p≤x≤q$p\le x\le q$, maka panjang kurva AB$AB$ adalah ∫pq1+(f′(x))2‾‾‾‾‾‾‾‾‾‾‾√dx$\underset{p}{\overset{q}{\int }}\sqrt{1+{\left(f^{\prime }(x)\right)}^2}dx$.
• Jika titik A(p,r)$A(p,r)$ dan B(q,s)$B(q,s)$ terletak pada kurva x=g(y)$x=g(y)$ dan g′(y)$g^{\prime }(y)$ kontinu pada interval r≤y≤s$r\le y\le s$, maka panjang kurva AB$AB$ adalah ∫rs1+(g′(y))2‾‾‾‾‾‾‾‾‾‾‾√dy$\underset{r}{\overset{s}{\int }}\sqrt{1+{\left(g^{\prime }(y)\right)}^2}dy$.
• Jika titik A$A$ dan B$B$ terletak pada kurva dengan persamaan parameter x(t)$x(t)$ dan y(t)$y(t)$, serta x′(t)$x^{\prime }(t)$ dan y′(t)$y^{\prime }(t)$ kontinu pada interval t1≤t≤t2$t_1\le t\le t_2$, maka panjang kurva AB$AB$adalah ∫t1t2(x′(t))2+(y′(t))2‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾√dt$\underset{t_1}{\overset{t_2}{\int }}\sqrt{{\left(x^{\prime }(t)\right)}^2+{\left(y^{\prime }(t)\right)}^2}dt$.

Agar kalian semakin paham dengan materi di atas, yuk kita cermati contoh soal berikut.

Contoh

Berapakah panjang kurva x=y324+2y$x=\frac{y^3}{24}+\frac{2}{y}$ dari y=2$y=2$ sampai y=3$y=3$?

Penyelesaian:

Langkah pertama: menyederhanakan persamaan kurva.

x=y324+2y⇔x=124y3+2y−1$x=\frac{y^3}{24}+\frac{2}{y}\iff x=\frac{1}{24}{y}^3+2y^{-1}$

Langkah kedua: menentukan turunan pertama persamaan kurva

x′=18y2−2y−2$x^{\prime }=\frac{1}{8}{y}^2-2y^{-2}$

⇒1+(x′)2====1+(18y2−2y−2)21+164y4−12+4y−4164y4+12+4y−4(18y2+2y−2)2$\begin{array}{l}\Rightarrow \end{array}$

$\begin{array}{lll}1+{\left(x^{\prime }\right)}^2& =& 1+{\left(\frac{1}{8}{y}^2-2y^{-2}\right)}^2\\ & =& 1+\frac{1}{64}{y}^4-\frac{1}{2}+4y^{-4}\\ & =& \frac{1}{64}{y}^4+\frac{1}{2}+4y^{-4}\\ & =& {\left(\frac{1}{8}{y}^2+2y^{-2}\right)}^2\end{array}$

Langkah ketiga: menentukan panjang kurva

∫231+(x′)2‾‾‾‾‾‾‾‾√dy=====∫23(18y2+2y−2)2‾‾‾‾‾‾‾‾‾‾‾‾‾‾√dy∫23(18y2+2y−2)dy[124y3−2y−1]32124(27−8)−2(13−12)98$\begin{array}{l}\underset{}{\overset{}{<br>}}\end{array}$

$\begin{array}{lll}\underset{2}{\overset{3}{\int }}\sqrt{1+{\left(x^{\prime }\right)}^2}dy& =& \underset{2}{\overset{3}{\int }}\sqrt{{\left(\frac{1}{8}{y}^2+2y^{-2}\right)}^2}dy\\ & =& \underset{2}{\overset{3}{\int }}\left(\frac{1}{8}{y}^2+2y^{-2}\right)dy\\ & =& {\left[\frac{1}{24}{y}^3-2y^{-1}\right]}_{}^{}\end{array}$

$\begin{array}{l}{2}_3^{}\\ & =& \frac{1}{24}\left(27-8\right)-2\left(\frac{1}{3}-\frac{1}{2}\right)\\ & =& \frac{9}{8}\end{array}$

Berdasarkan uraian di atas, dapat disimpulkan bahwa panjang kurva x=y324+2y$x=\frac{y^3}{24}+\frac{2}{y}$ dari y=2$y=2$ sampai y=3$y=3$ adalah 98$\frac{9}{8}$ satuan panjang.

Yuk uji pemahaman kalian dengan mengerjakan sepuluh latihan soal dalam topik ini.