Refleksi terhadap Garis y = mx

Refleksi terhadap Garis y = mx -

Konsep Dasar

Pada topik sebelumnya, kalian telah belajar tentang refleksi terhadap sumbu X, refleksi terhadap sumbu Y, refleksi terhadap garis y = x, dan refleksi terhadap garis y = -x.

Kalian masih ingat bukan?

Nah, kali ini kalian akan belajar tentang refleksi terhadap garis y = mx. Sebagaimana telah kalian ketahui, garis y = mx adalah sebuah garis yang membentuk sudut tertentu dengan sumbu X positif dan m adalah gradien garis y = mx. Selanjutnya, jika besar sudut yang dimaksud adalah α$\alpha$, maka persamaan y = mx dapat dinyatakan dalam bentuk persamaan y=xtanα$y=x\tan \alpha$.

Bagaimanakah bentuk matriks transformasi refleksi terhadap garis y = mx?

Matriks transformasi refleksi terhadap garis y = mx berordo 2 x 2, sebab hanya ada dua variabel dalam persamaan garis tersebut. Nah, untuk menjawab pertanyaan di atas, kita perlu menentukan terlebih dahulu bayangan titik (1, 0) dan titik (0, 1) oleh refleksi terhadap garis y = mx. Perlu kalian ketahui, kedua titik tersebut diperoleh dari matriks identitas berordo 2 x 2, yaitu (1001 )$\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)$.

Bayangan titik A(1, 0) terhadap refleksi garis y = mx

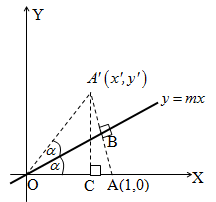
Pada gambar di atas, refleksi titik A(1, 0) terhadap garis y = mx adalah A'(x', y'). Adapun besar sudut antara titik A (sumbu X positif) dengan garis y = mx adalah ∠AOB=α$\mathrm{\angle }AOB=\alpha$.

Oleh karena besar sudut yang dibuat oleh titik bayangan dengan garis y = mx sama, maka ∠AOA′=2α$\mathrm{\angle }AO{A}^{\prime }=2\alpha$.

Selanjutnya, karena ∆OA'C siku-siku di C dan OA' = 1, maka

OC===OA′×cos2α1×cos2αcos2α $\begin{array}{lll}OC& =& O{A}^{\prime }\times \cos 2\alpha \\ & =& 1\times \cos 2\alpha \\ & =& \cos 2\alpha \end{array}$

A′C===OA′×sin2α1×sin2αsin2α $\begin{array}{lll}{A}^{\prime }C& =& O{A}^{\prime }\times \sin 2\alpha \\ & =& 1\times \sin 2\alpha \\ & =& \sin 2\alpha \end{array}$

Dengan demikian, dapat ditarik kesimpulan bahwa koordinat titik bayangan dari titikA(1, 0) terhadap garis y = mx adalah A′(x′,y′)=A′(cos2α,sin2α)$A^{\prime }(x^{\prime },y^{\prime })=A^{\prime }(\cos 2\alpha ,\sin 2\alpha )$.

Jadi, kolom pertama dari matriks transformasi refleksi terhadap garis y = mx adalah (cos2αsin2α )$\left(\begin{array}{c}\cos 2\alpha \\ \sin 2\alpha \end{array}\right)$.

Bayangan titik A(0, 1) terhadap refleksi garis y = mx

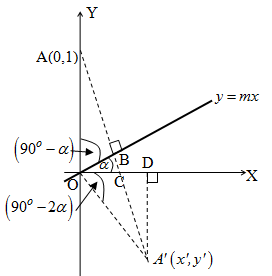
Pada gambar di atas, refleksi titik A(0, 1) terhadap garis y = mx adalah A'(x', y'). Adapun besar sudut antara sumbu X positif dengan garis y = mx adalah ∠COB=α$\mathrm{\angle }COB=\alpha$.

Oleh karena ∠COB=α$\mathrm{\angle }COB=\alpha$, maka ∠BOA=90°−α=∠BOA′ $\mathrm{\angle }BOA=90°-\alpha =\mathrm{\angle }BO{A}^{\prime }$, sehingga ∠COA′=∠BOA′−∠COB=90°−2α$\mathrm{\angle }CO{A}^{\prime }=\mathrm{\angle }BO{A}^{\prime }-\mathrm{\angle }COB=90°-2\alpha$.

Selanjutnya karena ∆OA'D siku-siku di D dan OA' = 1, maka

• OD=OA′×cos(90°−2α)=1×sin2α=sin2α $OD=O{A}^{\prime }\times \cos (90°-2\alpha )=1\times \sin 2\alpha =\sin 2\alpha$
• DA′=−OA′×sin(90°−2α)=−1×cos2α=−cos2α$D{A}^{\prime }=-O{A}^{\prime }\times \sin (90°-2\alpha )=-1\times \cos 2\alpha =-\cos 2\alpha$

Dengan demikian, dapat ditarik kesimpulan bahwa koordinat titik bayangan dari titikA(0, 1) terhadap garis y = mx adalah A′(x′,y′)=A′(sin2α,−cos2α)$A^{\prime }(x^{\prime },y^{\prime })=A^{\prime }(\sin 2\alpha ,-\cos 2\alpha )$.

Jadi, kolom pertama dari matriks transformasi refleksi terhadap garis y = mx adalah (sin2α−cos2α )$\left(\begin{array}{c}\sin 2\alpha \\ -\cos 2\alpha \end{array}\right)$.

Nah, berdasarkan uraian di atas, apa yang dapat kalian simpulkan?

Ya, matriks transformasi refleksi terhadap garis y = mx adalah (cos2αsin2αsin2α−cos2α )$\left(\begin{array}{cc}\cos 2\alpha & \sin 2\alpha \\ \sin 2\alpha & -\cos 2\alpha \end{array}\right)$.

Jadi, untuk menentukan bayangan suatu titik, garis, ataupun kurva oleh refleksi terhadap garis y = mx, gunakanlah persamaan matriks berikut:

(x′y′ )=(cos2αsin2αsin2α−cos2α )(xy )$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{cc}\cos 2\alpha & \sin 2\alpha \\ \sin 2\alpha & -\cos 2\alpha \end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)$

Jika kalian ingat kembali konsep gradien sebagai tangen sebuah sudut, maka bentuk lain dari persamaan garis y = mx adalah y=xtanα$y=x\tan \alpha$. Selanjutnya, jika kalian perhatikan kembali bentuk matriks transformasi di atas, maka kalian akan menjumpai bentuk trigonometri sudut ganda, yaitu (2α)$(2\alpha )$.

Apakah kalian masih ingat dengan hubungan antara perbandingan trigonometri sudut tunggal dan sudut ganda?

Mari kita ingat kembali dengan mencermati tiga rumus berikut:

1. tanα=sinαcosα$\tan \alpha =\frac{\sin \alpha }{\cos \alpha }$
2. sin2α=2sinαcosα$\sin 2\alpha =2\sin \alpha \cos \alpha$
3. cos2α=cos2α−sin2α$\cos 2\alpha ={\cos }^2\alpha -{\sin }^2\alpha$

Agar kalian lebih mudah memahami materi ini, mari kita cermati beberapa contoh soal berikut.

Contoh 1

Tentukan bayangan titik (6, 2) jika direfleksikan terhadap garis y=3‾√x$y=\sqrt{3}x$.

Penyelesaian:

Persamaan garis y=3‾√x$y=\sqrt{3}x$ memiliki gradien m=3‾√$m=\sqrt{3}$ atau tanα=3‾√$\tan \alpha =\sqrt{3}$.

Dengan demikian, dapat kita gambarkan segitiga siku-siku sebagai berikut:

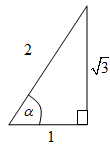
Berdasarkan gambar di atas, sinα=3√2 $\sin \alpha =\frac{\sqrt{3}}{2}$ dan cosα=12$\cos \alpha =\frac{1}{2}$.

Akibatnya,

sin2α====2sinαcosα2(3√2)(12)2(3√4)3√2 $\begin{array}{lll}\sin 2\alpha & =& 2\sin \alpha \cos \alpha \\ & =& 2\left(\frac{\sqrt{3}}{2}\right)\left(\frac{1}{2}\right)\\ & =& 2\left(\frac{\sqrt{3}}{4}\right)\\ & =& \frac{\sqrt{3}}{2}\end{array}$

cos2α$\cos 2\alpha$
=cos2α−sin2α$={\cos }^2\alpha -{\sin }^2\alpha$
=(12)2−(3√2)2$={\left(\frac{1}{2}\right)}^2-{\left(\frac{\sqrt{3}}{2}\right)}^2$
=14−34$=\frac{1}{4}-\frac{3}{4}$
=−12$=-\frac{1}{2}$

Selanjutnya, karena kita hendak menentukan bayangan dari titik (6, 2), maka (x, y) = (6, 2).

(x′y′ )====(cos2αsin2αsin2α−cos2α )(xy )(−12123‾√123‾√12 )(62 )(−3+3‾√33‾√+1 )(−3+3‾√1+33‾√ ) $\begin{array}{lll}\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)& =& \left(\begin{array}{cc}\cos 2\alpha & \sin 2\alpha \\ \sin 2\alpha & -\cos 2\alpha \end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)\\ & =& \left(\begin{array}{cc}-\frac{1}{2}& \frac{1}{2}\sqrt{3}\\ \frac{1}{2}\sqrt{3}& \frac{1}{2}\end{array}\right)\left(\begin{array}{c}6\\ 2\end{array}\right)\\ & =& \left(\begin{array}{c}-3+\sqrt{3}\\ 3\sqrt{3}+1\end{array}\right)\\ & =& \left(\begin{array}{c}-3+\sqrt{3}\\ 1+3\sqrt{3}\end{array}\right)\end{array}$

Berdasarkan uraian di atas, dapat disimpulkan bahwa bayangan titik (6, 2) oleh pencerminan terhadap garis y=3‾√x$y=\sqrt{3}x$ adalah (−3+3‾√,1+33‾√)$(-3+\sqrt{3},1+3\sqrt{3})$.

Contoh 2

Tentukan bayangan garis 2x – 4y = 5 oleh refleksi terhadap garis y = x tan 75°.

Penyelesaian:

Matriks transformasi refleksi yang sesuai adalah

(cos2αsin2αsin2α−cos2α )$\left(\begin{array}{cc}\cos 2\alpha & \sin 2\alpha \\ \sin 2\alpha & -\cos 2\alpha \end{array}\right)$ 
=(cos150°sin150°sin150°−cos150° )$=\left(\begin{array}{cc}\cos 150°& \sin 150°\\ \sin 150°& -\cos 150°\end{array}\right)$ 
=(−123‾√1212123‾√ )$=\left(\begin{array}{cc}-\frac{1}{2}\sqrt{3}& \frac{1}{2}\\ \frac{1}{2}& \frac{1}{2}\sqrt{3}\end{array}\right)$

Dengan demikian, kita peroleh persamaan matriks sebagai berikut:

(x′y′ )⇔(xy )⇔(xy )⇔(xy )====(−123‾√1212123‾√ )(xy )1−34−14(123‾√−12−12−123‾√ )(x′y′ )−(123‾√x′−12y′−12x′−123‾√y′ )(−123‾√x′+12y′12x′+123‾√y′ ) $\begin{array}{lll}\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)& =& \left(\begin{array}{cc}-\frac{1}{2}\sqrt{3}& \frac{1}{2}\\ \frac{1}{2}& \frac{1}{2}\sqrt{3}\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)\\ \iff \left(\begin{array}{c}x\\ y\end{array}\right)& =& \frac{1}{-\frac{3}{4}-\frac{1}{4}}\left(\begin{array}{cc}\frac{1}{2}\sqrt{3}& -\frac{1}{2}\\ -\frac{1}{2}& -\frac{1}{2}\sqrt{3}\end{array}\right)\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)\\ \iff \left(\begin{array}{c}x\\ y\end{array}\right)& =& -\left(\begin{array}{c}\frac{1}{2}\sqrt{3}{x}^{\prime }-\frac{1}{2}{y}^{\prime }\\ -\frac{1}{2}{x}^{\prime }-\frac{1}{2}\sqrt{3}{y}^{\prime }\end{array}\right)\\ \iff \left(\begin{array}{c}x\\ y\end{array}\right)& =& \left(\begin{array}{c}-\frac{1}{2}\sqrt{3}{x}^{\prime }+\frac{1}{2}{y}^{\prime }\\ \frac{1}{2}{x}^{\prime }+\frac{1}{2}\sqrt{3}{y}^{\prime }\end{array}\right)\end{array}$

Persamaan bayangan garis 2x – 4y = 5 oleh refleksi terhadap garis y = x tan 75° dapat ditentukan dengan cara mensubstitusikan variabel x dan y dari persamaan di atas ke dalam persamaan garis 2x – 4y = 5.

2x−4y=5⇔2(−123‾√x′+12y′)−4(12x′+123‾√y′)=5⇔−3‾√x′+y′−2x′−23‾√y′=5⇔(−2−3‾√)x′+(1−23‾√)y′=5  $\begin{array}{rl}& 2x-4y=5\\ & \iff 2(-\frac{1}{2}\sqrt{3}{x}^{\prime }+\frac{1}{2}{y}^{\prime })-4(\frac{1}{2}{x}^{\prime }+\frac{1}{2}\sqrt{3}{y}^{\prime })=5\\ & \iff -\sqrt{3}{x}^{\prime }+y^{\prime }-2x^{\prime }-2\sqrt{3}{y}^{\prime }=5\\ & \iff (-2-\sqrt{3})x^{\prime }+(1-2\sqrt{3})y^{\prime }=5\end{array}$

Berdasarkan uraian di atas, dapat disimpulkan bahwa persamaan bayangan garis 2x – 4y = 5 oleh refleksi terhadap garis y = x tan 75° adalah (−2−3‾√)x+(1−23‾√)y=5 $(-2-\sqrt{3})x+(1-2\sqrt{3})y=5$.

Untuk menguji pemahaman kalian, ayo kerjakan sepuluh latihan soal dalam topik ini.