Uji Hipotesis Satu Pihak

Uji Hipotesis Satu Pihak - Sebelumnya, kalian telah mempelajari ukuran pemusatan dan keragaman dalam statistika. Nah, dalam topik ini kalian akan mempelajari topik lain, yaitu mengenai uji hipotesis satu pihak. Untuk itu, mari kita dengan penuh semangat bersama-sama membahas lebih jauh mengenai topik ini.

1. HIPOTESIS STATISTIK

Pengujian hipotesis statistik merupakan salah satu bagian terpenting dalam statistika. Hal ini karena dalam kehidupan nyata kita seringkali diharuskan untuk membuat suatu keputusan atau kesimpulan mengenai suatu pemasalahan tertentu dalam populasi tertentu pula. Keputusan tersebut tentu tidak boleh diambil secara sembarangan. Sebelum mengambil suatu keputusan, terlebih dahulu kita harus membuat suatu dugaan mengenai masalah tersebut terhadap suatu populasi, kemudian menganalisa bukti-bukti yang ada. Dugaan mengenai satu atau lebih populasi dalam statistika disebut hipotesis statistik.

Keputusan untuk menolak atau menerima suatu hipotesis statistik tergantung pada konsistensi bukti-bukti yang kita peroleh. Suatu hipotesis statistik akan ditolak jika bukti-bukti yang diperoleh tidak mendukung hipotesis tersebut. Sebaliknya, jika bukti-bukti yang diperoleh secara konsisten mendukung hipotesis tersebut, maka hal ini akan membawa pada penerimaan hipotesis tersebut. Akan tetapi perlu dipahami bahwa penerimaan suatu hipotesis statistik tidak selalu berarti bahwa hipotesis tersebut benar. Karena menerima suatu hipotesis statistik sejatinya bermakna bahwa kita tidak memiliki cukup bukti untuk menolaknya.

Hipotesis yang dirumuskan dengan tujuan untuk ditolak diistilahkan dengan hipotesis nol dan dilambangkan dengan H₀ . Sedangkan hipotesis alternatifnya dilambangkan dengan H₁.

Contoh:

Akan diuji suatu pernyataan : “Suatu vitamin merk A lebih unggul dari vitamin yang telah beredar jika 75% orang yang mengonsumsinya mengalami peningkatan daya tahan tubuh”.
Tentukan rumusan hipotesisnya.

Penyelesaian:

Pernyataan tersebut dinyatakan sebagai H₁ , sedangkan lawan dari pernyataan tersebut dinyatakan sebagai H₀.

Sehingga, uji hipotesisnya dapat dituliskan sebagai berikut:

2. DAERAH PENOLAKAN

Daerah penolakan adalah daerah atau interval dimana H₀ ditolak.
Daerah penolakan disebut juga dengan daerah kritik.

3. TARAF NYATA

Taraf nyata atau adalah peluang terjadinya kesalahan yang berupa penerimaan H₀ yang salah.
Taraf nyata dapat pula dikatakan sebagai ukuran daerah kritik.
Apabila H₀ ditolak pada taraf nyata 0,05 maka uji tersebut dikatakan nyata.
Sedangkan jika H₀ ditolak pada taraf nyata 0,01 maka uji tersebut dikatakan sangat nyata.

4. STATISTIK UJI

Statistik uji atau disebut juga statistik penguji adalah variabel random yang digunakan untuk mengambil keputusan apakah H₀ ditolak atau tidak ditolak.
H₀ akan ditolak jika nilai statistik ujinya masuk ke dalam daerah kritiknya.

5. UJI HIPOTESIS SATU PIHAK

Uji hipotesis satu pihak merupakan uji hipotesis statistik yang hipotesis altenatifnya bersifat satu pihak saja. Uji hipotesis satu pihak dapat dirumuskan sebagai:

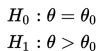
atau

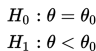
Hipotesis alternatif θ > θ₀ memiliki daerah kritik seluruhnya di ekor kanan sebarannya. Sedangkan daerah kritik dari hipotesis alternatif θ < θ₀ terletak pada ekor kanan sebarannya. H₀ selalu dinyatakan dalam bentuk kesamaan untuk menyatakan suatu nilai tunggal.

Contoh:

Sebuah perusahaan minuman instan menyatakan bahwa kadar gula rata-rata minuman hasil produksinya tidak lebih dari 12 gram per kemasan.
Tentukan hipotesis nol dan alternatif yang akan digunakan untuk menguji pernyataan perusahaan tersebut.
Tentukan pula daerah kritiknya.

Penyelesaian:

Pernyataan perusahaan minuman instan tersebut harus ditolak hanya jika μ > 12 gram dan harus diterima jika μ ≤ 12. Ingat bahwa H₀ harus menyatakan nilai tunggal, sehingga kita akan menguji:

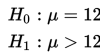
Meski H₀ dituliskan dengan tanda sama dengan, namun nilainya tidak hanya semata-mata tepat 12 gram. Akan tetapi nilai H₀ mencakup semua nilai yang tidak dicakup oleh H₁, yaitu tepat 12 gram atau kurang dari 12 gram.

Sehingga apabila menerima H₀, tidak boleh diartikan bahwa μ tepat bernilai 12 gram.

Menerima H₀ harus kita artikan bahwa kita tidak punya cukup bukti untuk menerima H₁.

Untuk menentukan daerah kritiknya, coba perhatikan hipotesis alternatifnya. Karena uji ini merupakan uji hipotesis satu pihak, maka lambang “lebih dari” menunjukkan bahwa daerah kritiknya berada di ekor kanan sebaran statistik X.

6. LANGKAH-LANGKAH UJI HIPOTESIS SATU PIHAK

Berikut ini adalah langkah-langkah yang dapat dilakukan untuk melakukan uji hipotesis satu pihak mengenai parameter populasi θ:

a. Nyatakan hipotesis nol nya, yaitu H₀ : θ = θ₀

b. Pilih hipotesis alternatif yang sesuai, yaitu H₁ : θ > θ₀ atau H₁ : θ <θ₀

c. Tentukan taraf nyata α

d. Pilih statistik uji yang sesuai, kemudian tentukan daerah kritiknya.

e. Hitung nilai statistik uji berdasarkan data sampelnya.

f. Keputusan: Jika nilai statistik ujinya jatuh pada daerah kritik, maka H₀ ditolak, sebaliknya jika nilai statistik ujinya di luar daerah kritik maka H₀ tidak ditolak.

7. UJI – t SATU SAMPEL

Uji t satu sampel digunakan untuk menentukan apakah nilai rata-rata sampel berbeda dengan nilai rata-rata acuan.

Bentuk hipotesis satu pihak untuk uji t satu sampel adalah sebagai berikut:

a. Bentuk uji hipotesis satu pihak untuk pihak kanan

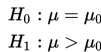
b. Bentuk uji hipotesis satu pihak untuk pihak kiri

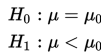
8. LANGKAH-LANGKAH UJI t SATU SAMPEL UNTUK UJI HIPOTESIS SATU PIHAK

a. Nyatakan hipotesis nol nya, yaitu:

b. Pilih hipotesis alternatif yang sesuai, yaitu:

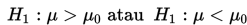
c. Tentukan taraf nyata

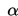
d. Tentukan nilai tabelnya, yaitu:

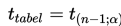
Keterangan:
n = banyaknya sampel 
(n − 1) = derajat bebas

e. Hitung nilai statistik uji berdasarkan data sampelnya, yaitu

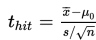
Keterangan:

f. Daerah kritik:

1. Jika hipotesis alternatifnya

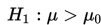
maka H₀ ditolak jika

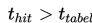
2. Jika hipotesis alternatifnya

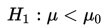
maka H₀ ditolak jika

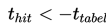
g. Keputusan: Jika nilai statistik ujinya jatuh pada daerah kritik, maka H₀ ditolak, sebaliknya jika nilai statistik ujinya di luar daerah kritik maka H₀ tidak ditolak.

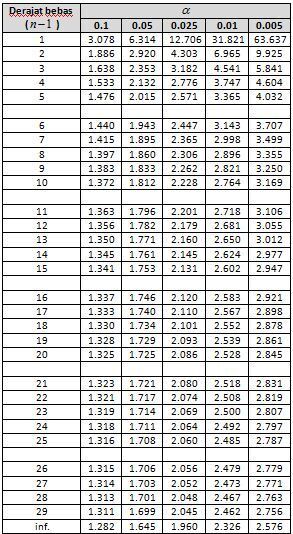
9. CARA MEMBACA TABEL UJI t

Cara menemukan nilai tabel pada tabel uji t adalah dengan memilih derajat bebas (n−1) dan

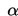
yang bersesuaian pada tabel uji t berikut ini.

Contoh:

Misal banyaknya sampel adalah 12 dan taraf signifikansinya adalah 0,05, maka nilai tabelnya yaitu

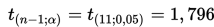
Contoh:

Waktu rata-rata yang diperlukan oleh siswa dalam mengerjakan satu set soal adalah 45 menit dengan simpangan baku 10 menit. Suatu set soal baru sedang dibuat. Untuk itu, dipilih secara acak 15 orang siswa untuk mengerjakan set soal baru tersebut. Ternyata, siswa-siswa tersebut memerlukan waktu rata-rata 40 menit dengan simpangan baku 12 menit untuk mengerjakan set soal baru tersebut. Dengan mengasumsikan bahwa populasi waktu yang diperlukan adalah normal dan menggunakan taraf signifikansi 0,05, ujilah bahwa nilai tengah populasinya sekarang kurang dari 45.

Jawab:

a. Hipotesis nol nya, yaitu: H₀ : μ = 45 menit

b. Hipotesis alternatif yang sesuai, yaitu: H₁ : μ < 45 menit

c. Taraf nyata

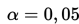
d. Nilai tabelnya, yaitu:

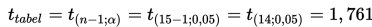
e. Nilai statistik uji berdasarkan data sampelnya, yaitu

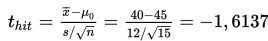
f. Daerah kritik:

Diperoleh bahwa

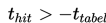
yaitu –1,6137 > –1,761

g. Keputusan:

Karena nilai statistik ujinya tidak jatuh pada daerah kritik, maka H₀ tidak ditolak. 
Berarti, fakta tidak cukup kuat untuk mendukung penyataan bahwa nilai tengah populasinya sekarang kurang dari 45 menit.