Refleksi terhadap Pusat Koordinat O(0,0)

Refleksi terhadap Pusat Koordinat O(0,0) - Halo adik-adik, bagaimana kabar kalian? 

Tetap semangat dalam belajar matematika bukan?

Dalam topik-topik sebelumnya kalian telah belajar mengenai refleksi (pencerminan). Nah, dalam topik ini kalian juga akan belajar tentang refleksi, yaitu refleksi terhadap pusat koordinat O(0, 0).

Nah, apa perbedaannya dengan topik-topik sebelumnya?

Mari kita temukan jawabannya dalam topik ini.

Konsep Dasar

Hasil refleksi titik A(x, y) terhadap pusat koordinat O(0, 0) digambarkan dalam ilustrasi berikut:

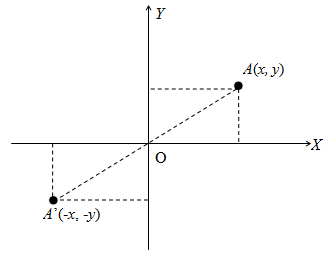
Dalam ilustrasi di atas, tampak bahwa koordinat bayangan dari titik A(x, y) adalah titikA'(x', y') = A'(-x, -y) .

Nah, transformasi refleksi tersebut dapat dituliskan dalam notasi berikut: A(x,y)−→−−−MO(0,0)A′(−x,−y)$A(x,y)\stackrel{M_{O(0,0)}}{\to }{A}^{\prime }(-x,-y)$.

Tahukah kalian bentuk matriks transformasi yang sesuai dengan refleksi terhadap pusat koordinat O(0, 0)?

Mari kita perhatikan uraian berikut.

Oleh karena hasil refleksi titik A(x, y) adalah titik A'(x', y') = A'(-x, -y) , maka

• x' = -x = (-1)x + (0)y
• y' = -y = (0)x + (-1)y

Dengan demikian, kita peroleh persamaan matriks berikut:

(x′y′ )=(−100−1 )(xy )$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{cc}-1& 0\\ 0& -1\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)$

Berdasarkan uraian di atas, dapat kita simpulkan bahwa matriks transformasi yang sesuai dengan refleksi terhadap pusat koordinat O(0, 0) adalah M=(−100−1 ) $M=\left(\begin{array}{cc}-1& 0\\ 0& -1\end{array}\right)$.

Materi di atas mudah dipahami bukan?

Agar kalian semakin paham, mari kita cermati beberapa contoh berikut.

Contoh 1

Tentukan bayangan titik P(2, 5) oleh refleksi terhadap titik pusat O(0, 0).

Penyelesaian:

Koordinat titik bayangan dapat ditentukan dengan menggunakan persamaan matirks berikut:

(x′y′ )====(−100−1 )(xy )(−100−1 )(25 )(−2+00−5 )(−2−5 ) $\begin{array}{lll}\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)& =& \left(\begin{array}{cc}-1& 0\\ 0& -1\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)\\ & =& \left(\begin{array}{cc}-1& 0\\ 0& -1\end{array}\right)\left(\begin{array}{c}2\\ 5\end{array}\right)\\ & =& \left(\begin{array}{c}-2+0\\ 0-5\end{array}\right)\\ & =& \left(\begin{array}{c}-2\\ -5\end{array}\right)\end{array}$

Berdasarkan uraian di atas, dapat kita simpulkan bahwa bayangan titik P(2, 5) oleh refleksi terhadap titik pusat O(0, 0) adalah P’(–2, –5).

Contoh 2

Diketahui ∆ABC dengan koordinat ketiga titik sudutnya adalah A(0, 1), B(2, 3), dan C(5, 0). Tentukan bayangan ketiga koordinat titik sudut ∆ABC oleh refleksi terhadap pusat koordinat O(0, 0).

Penyelesaian:

Bayangan titik A, B, dan C oleh refleksi terhadap titik pusat koordinat O(0, 0) dapat ditentukan dengan menggunakan persamaan matirks berikut:

X====(−100−1 )(xAyAxByBxCyC )(−100−1 )(012350 )(0+00−1−2+00−3−5+00+0 )(0−1−2−3−50 ) $\begin{array}{lll}X& =& \left(\begin{array}{cc}-1& 0\\ 0& -1\end{array}\right)\left(\begin{array}{ccc}{x}_A& x_B& x_C\\ y_A& y_B& y_C\end{array}\right)\\ & =& \left(\begin{array}{cc}-1& 0\\ 0& -1\end{array}\right)\left(\begin{array}{lll}0& 2& 5\\ 1& 3& 0\end{array}\right)\\ & =& \left(\begin{array}{lll}0+0& -2+0& -5+0\\ 0-1& 0-3& 0+0\end{array}\right)\\ & =& \left(\begin{array}{lll}0& -2& -5\\ -1& -3& 0\end{array}\right)\end{array}$

Berdasarkan uraian di atas, dapat disimpulkan bahwa bayangan titik A, B, dan C oleh refleksi terhadap titik pusat koordinat O(0, 0) adalah A’(0, –1), B’(–2, –3), dan C’(–5, 0).

Contoh 3

Tentukan bayangan garis y = 4x – 3 oleh refleksi terhadap titik pusat koordinat O(0, 0).

Penyelesaian:

Oleh karena bayangan titik (x, y) oleh refleksi terhadap pusat koordinat O(0, 0) adalah(x', y') = (-x, -y), maka dengan mensubtitusikan x = -x' dan y = -y' ke persamaan garis y = 4x – 3, kita peroleh persamaan bayangan berikut:

y⇔−y′⇔−y′⇔y′====4x−34(−x′)−3−4x′−34x′+3 $\begin{array}{lll}y& =& 4x-3\\ \iff -y^{\prime }& =& 4(-x^{\prime })-3\\ \iff -y^{\prime }& =& -4x^{\prime }-3\\ \iff y^{\prime }& =& 4x^{\prime }+3\end{array}$

Jadi, bayangan garis y = 4x – 3 oleh refleksi terhadap titik pusat koordinat O(0, 0) adalahy = 4x + 3.

Nah, apakah kalian tahu cara mencari koordinat titik semula jika koordinat titik bayangan telah diketahui?

Mari kita temukan jawabannya dengan mencermati contoh 4 berikut.

Contoh 4

Diketahui titik R’(–8, 5) adalah bayangan dari titik R(x, y) oleh refleksi terhadap titik pusat koordinat O(0, 0). Tentukan koordinat titik R.

Penyelesaian:

Oleh karena bayangan titik (x, y) oleh refleksi terhadap pusat koordinat O(0, 0) adalah (-x, -y), maka

• -x = -8 ⇔ x = 8
• -y = 5 ⇔ y = -5

Jadi, koordinat titik R adalah (8, –5).

Dalam topik ini ada sepuluh latihan soal. Ayo uji pemahaman kalian dengan mengerjakan latihan soal tersebut.