Persamaan Vektor dari Sebuah Garis Lurus

Persamaan Vektor dari Sebuah Garis Lurus - Pada waktu kalian masih SMP, kalian telah belajar tentang cara menentukan gradien suatu garis, cara menentukan persamaan garis melalui sebuah titik jika diketahui gradien, maupun cara menentukan persamaan garis melalui dua titik.

Masih ingatkah kalian dengan materi tersebut?

Perlu kalian ketahui, materi di atas akan kita gunakan untuk memperlajari topik ini.

Konsep Dasar

Tahukah kalian hubungan antara vektor dan persamaan garis lurus?

Yuk kita temukan jawabannya dengan memperhatikan ilustrasi berikut.

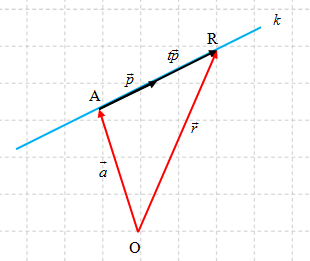
Pada ilustrasi di atas, tampak bahwa garis k$k$ melalui titik A$A$ dengan arah vektor p⃗ $\overrightarrow{p}$, dimana p⃗ $\overrightarrow{p}$ bukanlah vektor nol

Nah, karena titik R$R$ terletak pada garis k$k$, maka perpindahan vektor AR−→$\overrightarrow{AR}$ merupakan kelipatan dari vektor p⃗ $\overrightarrow{p}$ → AR−→=tp⃗ $\overrightarrow{AR}=t\overrightarrow{p}$.

Selanjutnya, dengan memperhatikan arah vektor, kita peroleh hubungan sebagai berikut:

r⃗ ===OR−→−OA−→−+AR−→a⃗ +tp⃗ $\begin{array}{lll}\overrightarrow{r}& =& \overrightarrow{OR}\\ & =& \overrightarrow{OA}+\overrightarrow{AR}\\ & =& \overrightarrow{a}+t\overrightarrow{p}\end{array}$

Perlu kalian ketahui, a⃗ $\overrightarrow{a}$ adalah vektor posisi dari titik A$A$ dan t$t$ adalah skalar yang menyatakan rasio perpindahan vektor AR−→$\overrightarrow{AR}$ terhadap p⃗ $\overrightarrow{p}$.

Jadi, apa hubungan antara vektor dan persamaan garis lurus?

Ya, persamaan vektor dari sebuah garis yang melalui titik A$A$ dengan arah vektor p⃗ $\overrightarrow{p}$adalah r⃗ =a⃗ +tp⃗ $\overrightarrow{r}=\overrightarrow{a}+t\overrightarrow{p}$.

Materi di atas mudah dipahami bukan?

Nah, agar kalian semakin jelas dengan materi di atas, mari kita cermati beberapa contoh berikut.

Contoh 1

Tentukan persamaan vektor dari sebuah garis yang melalui titik A(1,2)$A(1,2)$ dengan gradien m=45$m=\frac{4}{5}$.

Penyelesaian:

Oleh karena gradien garis adalah m=45$m=\frac{4}{5}$, maka ΔyΔx=45$\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}=\frac{4}{5}$. Akibatnya, arah vektor adalahp⃗ =(54)$\overrightarrow{p}=\left(\begin{array}{c}5\\ 4\end{array}\right)$.

Dengan demikian, persamaan vektor dari garis yang dimaksud adalah

r⃗ ⇔(xy)⇔(xy)===a⃗ +tp⃗ (12)+t(54)(1+5t2+4t)$\begin{array}{lll}\overrightarrow{r}& =& \overrightarrow{a}+t\overrightarrow{p}\\ \iff \left(\begin{array}{c}x\\ y\end{array}\right)& =& \left(\begin{array}{c}1\\ 2\end{array}\right)+t\left(\begin{array}{c}5\\ 4\end{array}\right)\\ \iff \left(\begin{array}{c}x\\ y\end{array}\right)& =& \left(\begin{array}{c}1+5t\\ 2+4t\end{array}\right)\end{array}$

Berdasarkan uraian di atas,

• x=1+5t$x=1+5t$
• y=2+4t$y=2+4t$

Jika kita eliminasi variabel t$t$ dari sistem persamaan di atas, maka kita peroleh persamaan garis 4x−5y=−6$4x-5y=-6$.

Jadi, persamaan vektor dari sebuah garis yang melalui titik A(1,2)$A(1,2)$ dengan gradien m=45$m=\frac{4}{5}$ adalah 4x−5y=−6$4x-5y=-6$.

Pada contoh 1 di atas, kalian telah belajar cara mengubah persamaan vektor menjadi persamaan garis dalam sistem Cartesian. Nah, pada contoh 2 berikut, kalian akan belajar cara megubah persamaan garis dalam sistem Cartesian ke dalam persamaan vektor.

Contoh 2

Tentukan persamaan vektor dari garis 2x+3y=12$2x+3y=12$.

Penyelesaian:

Langkah I: menentukan gradien garis.

Oleh karena gradien garis ax+by=c$ax+by=c$ adalah m=−ab$m=-\frac{a}{b}$, maka gradien garis 2x+3y=12$2x+3y=12$ adalah m=−23$m=-\frac{2}{3}$.

Langkah II: menentukan arah vektor.

Oleh karena m=−23$m=-\frac{2}{3}$, maka ΔyΔx=−23$\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}=-\frac{2}{3}$. Akibatnya, arah vektor adalah p⃗ =(−32)$\overrightarrow{p}=\left(\begin{array}{c}-3\\ 2\end{array}\right)$.

Langkah III: menentukan titik yang terletak pada garis.

Oleh karena 2(3)+3(2)=12$2(3)+3(2)=12$, maka titik A(3,2)$A(3,2)$ terletak pada garis 2x+3y=12$2x+3y=12$.

Langkah IV: menentukan persamaan vektor dari garis 2x+3y=12$2x+3y=12$.

r⃗ ==a⃗ +tp⃗ (32)+t(−32)$\begin{array}{lll}\overrightarrow{r}& =& \overrightarrow{a}+t\overrightarrow{p}\\ & =& \left(\begin{array}{c}3\\ 2\end{array}\right)+t\left(\begin{array}{c}-3\\ 2\end{array}\right)\end{array}$

Jadi, persamaan vektor dari garis 2x+3y=12$2x+3y=12$ adalah r⃗ =(32)+t(−32)$\overrightarrow{r}=\left(\begin{array}{c}3\\ 2\end{array}\right)+t\left(\begin{array}{c}-3\\ 2\end{array}\right)$.

Nah, pada contoh 3 ini kalian akan belajar menentukan koordinat titik potong dua garis.

Contoh 3

Tentukan koordinat titik potong antara garis r⃗ =(34)+m(21)$\overrightarrow{r}=\left(\begin{array}{c}3\\ 4\end{array}\right)+m\left(\begin{array}{c}2\\ 1\end{array}\right)$ dan r⃗ =(42)+n(34)$\overrightarrow{r}=\left(\begin{array}{c}4\\ 2\end{array}\right)+n\left(\begin{array}{c}3\\ 4\end{array}\right)$.

Penyelesaian:

Oleh karena

• r⃗ =(34)+m(21)=(3+2m4+m)$\overrightarrow{r}=\left(\begin{array}{c}3\\ 4\end{array}\right)+m\left(\begin{array}{c}2\\ 1\end{array}\right)=\left(\begin{array}{c}3+2m\\ 4+m\end{array}\right)$
• r⃗ =(42)+n(34)=(4+3n2+4n)$\overrightarrow{r}=\left(\begin{array}{c}4\\ 2\end{array}\right)+n\left(\begin{array}{c}3\\ 4\end{array}\right)=\left(\begin{array}{c}4+3n\\ 2+4n\end{array}\right)$

maka

• 3+2m=4+3n⇔2m−3n=1$3+2m=4+3n\iff 2m-3n=1$
• 4+m=2+4n⇔m−4n=−2$4+m=2+4n\iff m-4n=-2$

Jika kita gunakan metode eliminasi dan subtitusi, maka kita peroleh bahwa m=2$m=2$ dan n=1$n=1$.

Dengan demikian,

r⃗ =(3+2m4+m)=(3+44+2)=(76)$\overrightarrow{r}=\left(\begin{array}{c}3+2m\\ 4+m\end{array}\right)=\left(\begin{array}{c}3+4\\ 4+2\end{array}\right)=\left(\begin{array}{c}7\\ 6\end{array}\right)$

r⃗ =(4+3n2+4n)=(4+32+4)=(76)$\overrightarrow{r}=\left(\begin{array}{c}4+3n\\ 2+4n\end{array}\right)=\left(\begin{array}{c}4+3\\ 2+4\end{array}\right)=\left(\begin{array}{c}7\\ 6\end{array}\right)$

Jadi, koordinat titik potong yang dimaksud adalah (7,6)$(7,6)$.

Nah, jika kalian menemukan soal terkait persamaan vektor dari dua buah garis sejajar, maka perlu kalian ingat bahwa dua buah garis sejajar mempunyai gradien sama. Adapun hasil kali gradien dua garis yang saling tegak lurus adalah negatif satu.

Yuk kerjakan sepuluh latihan soal yang ada dalam topik ini untuk menguji pemahaman kalian.