Perkalian Skalar Dua Vektor

Perkalian Skalar Dua Vektor - Konsep perkalian merupakan suatu konsep matematika yang sudah pasti kalian kuasai dengan baik. Akan tetapi, tahukah kalian bahwa perkalian memiliki arti yang berbeda pada konteks yang berbeda? Misalnya pada perkalian antarbilangan real dan perkalian antarmatriks, keduanya jelas memiliki konsep perkalian yang berbeda bukan? Nah, selain pada bilangan real dan matriks, perkalian juga berlaku pada vektor.

        Pada topik sebelumnya, kalian telah belajar tentang perkalian suatu vektor dengan skalar. Perkalian suatu vektor dengan skalar menghasilkan suatu besaran vektor yang baru. Tahukan kalian bahwa tidak semua operasi yang melibatkan besaran vektor selalu menghasilkan vektor? Lantas, operasi vektor seperti apakah yang tidak menghasilkan vektor? Pada topik ini, kalian akan mempelajari operasi tersebut, yaitu operasi perkalian skalar dua vektor atau biasa dikenal dengan sebutan dot product(inner product). Perkalian ini dilambangkan dengan "⋅$\cdot$". Untuk memahaminya, mari simak topik ini dengan saksama ya.

💢 Definisi Perkalian Skalar Dua Vektor

☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳

Operasi perkalian skalar dua vektor didefinisikan sebagai kombinasi linear atau penjumlahan hasil kali komponen-komponen vektor tersebut. Misalkan vektor A⃗ =⟨a1,a2,a3,....,an⟩$\overrightarrow{A}=⟨a_1,a_2,a_3,....,a_n⟩$ dan B⃗ =⟨b1,b2,b3,....,bn⟩$\overrightarrow{B}=⟨b_1,b_2,b_3,....,b_n⟩$ sama-sama berdimensi n. Perkalian skalar dari A⃗ $\overrightarrow{A}$ dan B⃗ $\overrightarrow{B}$ didefinisikan sebagai:

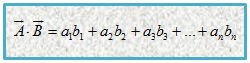
        Perlu kalian pahami dengan baik bahwa, hasil dari perkalian skalar ini bukan suatu vektor, melainkan suatu bilangan real. Oleh karena itu, penyelesaian dengan pendekatan grafis tidak terlalu banyak membantu seperti pada operasi-operasi vektor sebelumnya.

Untuk lebih jelasnya, pehatikan contoh berikut ini.

♫ Contoh

﹌﹌﹌﹌﹌﹌﹌﹌

⓵ Jika A⃗ =⟨a1,a2⟩$\overrightarrow{A}=⟨a_1,a_2⟩$ dan B⃗ =⟨b1,b2⟩$\overrightarrow{B}=⟨b_1,b_2⟩$ vektor-vektor yang berada dalam R2 , maka:

A⃗ ⋅B⃗ =a1b1+a2b2$\overrightarrow{A}\cdot \overrightarrow{B}=a_1{b}_1+a_2{b}_2$

⓶ Jika A⃗ =⟨a1,a2,a3⟩$\overrightarrow{A}=⟨a_1,a_2,a_3⟩$ dan B⃗ =⟨b1,b2,b3⟩$\overrightarrow{B}=⟨b_1,b_2,b_3⟩$ vektor-vektor yang berada dalam R3 , maka:

A⃗ ⋅B⃗ =a1b1+a2b2+a3b3$\overrightarrow{A}\cdot \overrightarrow{B}=a_1{b}_1+a_2{b}_2+a_3{b}_3$

Untuk vektor-vektor dengan dimensi yang lebih tinggi, kalian juga dapat menggunakan cara yang sama.

☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳

💢 Definisi Lain Perkalian Skalar Dua Vektor

☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳

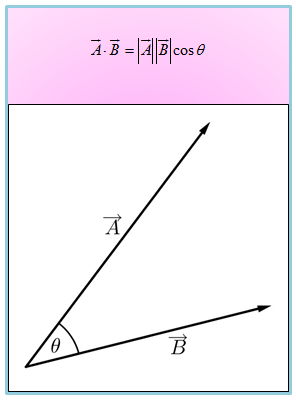
Perkalian skalar dua vektor juga dapat didefinisikan sebagai hasil perkalian antara panjang kedua vektor dan kosinus sudut di antara kedua vektor tersebut.

        Jika A⃗ $\overrightarrow{A}$ dan B⃗ $\overrightarrow{B}$ vektor-vektor tak nol dan θ sudut di antara vektor A⃗ $\overrightarrow{A}$ dan B⃗ $\overrightarrow{B}$, maka perkalian skalar dari kedua vektor ini dapat didefinisikan dengan:

☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳

☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳

⓵ Diketahui vektor A⃗ =⟨3,4⟩$\overrightarrow{A}=⟨3,4⟩$. Hitunglah nilai dari A⃗ ⋅A⃗ $\overrightarrow{A}\cdot \overrightarrow{A}$.

Penyelesaian:

Perkalian skalar dua vektor merupakan kombinasi linear atau penjumlahan hasil kali komponen-komponen vektor tersebut. Dengan demikian, nilai dari pekalian A⃗ ⋅A⃗ $\overrightarrow{A}\cdot \overrightarrow{A}$adalah:

A⃗ ⋅A⃗ ====⟨3,4⟩⋅⟨3,4⟩(3×3)+(4×4)9+1625$\begin{array}{lll}\overrightarrow{A}\cdot \overrightarrow{A}& =& ⟨3,4⟩\cdot ⟨3,4⟩\\ & =& (3\times 3)+(4\times 4)\\ & =& 9+16\\ & =& 25\end{array}$

Jadi, nilai dari A⃗ ⋅A⃗ $\overrightarrow{A}\cdot \overrightarrow{A}$ adalah 25.

⓶ Jika A⃗ =⟨1,5,−2,4⟩$\overrightarrow{A}=⟨1,5,-2,4⟩$ dan B⃗ =⟨2,3,8,−1⟩$\overrightarrow{B}=⟨2,3,8,-1⟩$, maka nilai dari A⃗ ⋅B⃗ $\overrightarrow{A}\cdot \overrightarrow{B}$ adalah ....

Penyelesaian:

Perkalian skalar dua vektor merupakan kombinasi linear atau penjumlahan hasil kali komponen-komponen vektor tersebut. Dengan demikian, nilai dari pekalian A⃗ ⋅B⃗ $\overrightarrow{A}\cdot \overrightarrow{B}$adalah:

A⃗ ⋅B⃗ ====⟨1,5,−2,4⟩⋅⟨2,3,8,−1⟩(1×2)+(5×3)+(−2×8)+(4×−1)2+15+(−16)+(−4)−3$\begin{array}{l}\stackrel{}{\mathrm{<br>}}\end{array}$

$\begin{array}{lll}\overrightarrow{A}\cdot \overrightarrow{B}& =& ⟨1,5,-2,4⟩\cdot ⟨2,3,8,-1⟩\\ & =& (1\times 2)+(5\times 3)+(-2\times 8)+(4\times -1)\\ & =& 2+15+(-16)+(-4)\\ & =& -3\end{array}$

Jadi, nilai dari A⃗ ⋅B⃗ $\overrightarrow{A}\cdot \overrightarrow{B}$ adalah -3.

⓷ Diketahui vektor A⃗ =⟨2,3⟩$\overrightarrow{A}=⟨2,3⟩$ dan B⃗ =⟨1,2⟩$\overrightarrow{B}=⟨1,2⟩$. Jika terdapat suatu vektor C⃗ $\overrightarrow{C}$sedemikian sehingga A⃗ ⋅C⃗ =22$\overrightarrow{A}\cdot \overrightarrow{C}=22$ dan B⃗ ⋅C⃗ =14$\overrightarrow{B}\cdot \overrightarrow{C}=14$, maka vektor C⃗ $\overrightarrow{C}$ yang dimaksud adalah ....

Penyelesaian:

Misalkan vektor C⃗ $\overrightarrow{C}$ kita nyatakan sebagai C⃗ =⟨x,y⟩$\overrightarrow{C}=⟨x,y⟩$. Dengan demikian, kedua perkalian skalar dua vektor tersebut dapat kita tulis sebagai berikut.

A⃗ ⋅C⃗ ⟨2,3⟩⋅⟨x,y⟩2x+3y===222222...(1)$\begin{array}{lll}\overrightarrow{A}\cdot \overrightarrow{C}& =& 22\\ ⟨2,3⟩\cdot ⟨x,y⟩& =& 22\\ 2x+3y& =& \mathrm{22...}(1)\end{array}$

B⃗ ⋅C⃗ ⟨1,2⟩⋅⟨x,y⟩x+2y===141414...(2)$\begin{array}{lll}\overrightarrow{B}\cdot \overrightarrow{C}& =& 14\\ ⟨1,2⟩\cdot ⟨x,y⟩& =& 14\\ x+2y& =& \mathrm{14...}(2)\end{array}$

Persamaan (1) dan (2) di atas membentuk sistem persamaan linear dua variabel. Untuk menentukan nilai x dan y dari sistem persamaan tersebut, kita dapat menggunakan metode eliminasi substitusi berikut ini.

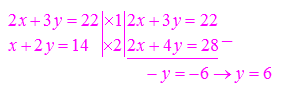
Substitusikan y = 6 ke dalam persamaan 2x + 3y = 22, sehingga didapat:

2x + 3(6) = 22

⇔2x + 18 = 22

⇔2x = 4

⇔x = 2

Jadi, vektor C⃗ =⟨2,6⟩$\overrightarrow{C}=⟨2,6⟩$.