Sudut antara Dua Vektor

Sudut antara Dua Vektor - Pada topik sebelumnya, kita telah belajar tentang perkalian skalar dua vektor. Pada topik tersebut, kita telah menyinggung sedikit tentang sudut antara dua vektor. Sebelum membahas lebih jauh tentang sudut antara dua vektor, apakan kalian masih ingat dengan gambar di bawah ini?

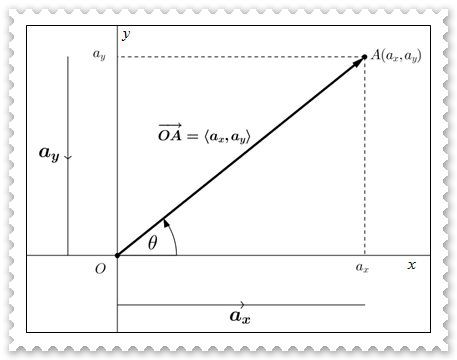
        Ya, gambar di atas telah kalian jumpai pada topik penjumlahan, pengurangan, dan panjang vektor. Jika vektor OA→$\overrightarrow{OA}$ membentuk sudut θ terhadap sumbu x positif dan komponen dari vektor OA→$\overrightarrow{OA}$ diketahui, maka kita dapat dengan mudah menghitung besar sudut θ. Perhitungan sudut θ dapat kita lakukan dengan memanfaatkan ilmu trigonometri dasar, yaitu dengan invers tangen sudut θ berikut ini.

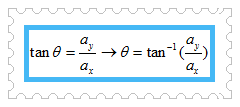
        Cukup sederhana bukan? Nah, bagaimana jika sudut yang akan ditentukan berada di antara dua vektor? Misalnya sudut antara vektor OA→$\overrightarrow{OA}$ dan OB→$\overrightarrow{OB}$ yang komponen keduanya diketahui? Untuk mengetahui jawabannya, mari simak topik ini dengan saksama.

♕ KONSEP

▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩

Perhatikan gambar di bawah ini.

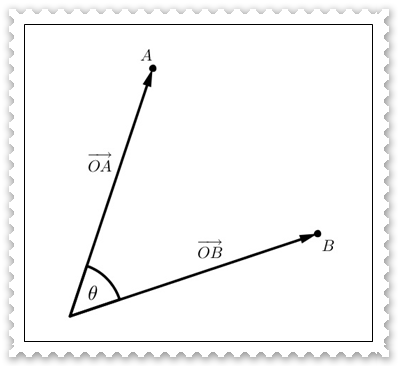
        Pada dimensi 2 dan 3, penentuan sudut antara dua vektor seperti gambar di atas dapat dilakukan dengan cara menggambar vektor-vektor pada koordinat Cartesius, kemudian mengukurnya dengan alat ukur sudut. Namun, cara ini tidak dapat lagi dilakukan pada dimensi yang lebih tinggi. Oleh karena itu, kita memerlukan suatu cara untuk menentukan besar sudut antara dua vektor secara umum.

        Setelah mempelajari konsep tentang perkalian skalar dua vektor pada topik sebelumnya, kalian tentu masih ingat dengan definisi perkalian skalar antara dua vektor berikut ini.

Jika A⃗ $\overrightarrow{A}$ dan B⃗ $\overrightarrow{B}$ vektor-vektor tak nol dan θ sudut di antara vektor A⃗ $\overrightarrow{A}$ dan B⃗ $\overrightarrow{B}$, maka perkalian skalar dari kedua vektor ini dapat didefinisikan dengan:

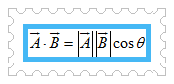
Dari definisi tersebut, dapat kita peroleh:

A⃗ ⋅B⃗ ⇔A⃗ ⋅B⃗ ∣∣A⃗ ∣∣∣∣B⃗ ∣∣⇔cosθ===∣∣A⃗ ∣∣∣∣B⃗ ∣∣cosθcosθA⃗ ⋅B⃗ ∣∣A⃗ ∣∣∣∣B⃗ ∣∣$\begin{array}{lll}\overrightarrow{A}\cdot \overrightarrow{B}& =& \left|\overrightarrow{A}\right|\left|\overrightarrow{B}\right|\cos \theta \\ \iff \frac{\overrightarrow{A}\cdot \overrightarrow{B}}{\left|\overrightarrow{A}\right|\left|\overrightarrow{B}\right|}& =& \cos \theta \\ \iff \cos \theta & =& \frac{\overrightarrow{A}\cdot \overrightarrow{B}}{\left|\overrightarrow{A}\right|\left|\overrightarrow{B}\right|}\end{array}$

        Dari persamaan di atas, dapat kita simpulkan bahwa untuk menentukan besar sudut antara dua vektor dapat dilakukan dengan menghitung invers dari kosinus berikut.

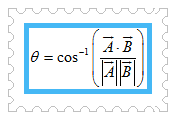
        Kelebihan dari persamaan terakhir ini adalah kita dapat menghitung besar sudut antara dua vektor dalam dimenesi berapapun. Selama kedua vektor dinyatakan dalam komponen vektor, maka penentuan besar sudut antara keduanya selalu mungkin dilakukan.
▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩

Agar kalian dapat memahami penggunaan rumus tersebut, mari perhatikan beberapa contoh berikut.

▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩

♫ Contoh 1

Hitunglah besar sudut antara vektor A⃗ =⟨1,1⟩$\overrightarrow{A}=⟨1,1⟩$ dan vektor B⃗ =⟨0,1⟩$\overrightarrow{B}=⟨0,1⟩$.

♫ Penyelesaian:

Untuk menentukan besar sudut antara kedua vektor tersebut, terlebih dahulu hitunglah perkalian skalar kedua vektor dan panjang masing-masing vektor.

Perkalian skalar kedua vektor:

A⃗ ⋅B⃗ =⟨1,1⟩⋅⟨0,1⟩A⃗ ⋅B⃗ =1×0+1×1A⃗ ⋅B⃗ =0+1A⃗ ⋅B⃗ =1$\begin{array}{l}\overrightarrow{A}\cdot \overrightarrow{B}=⟨1,1⟩\cdot ⟨0,1⟩\\ \overrightarrow{A}\cdot \overrightarrow{B}=1\times 0+1\times 1\\ \overrightarrow{A}\cdot \overrightarrow{B}=0+1\\ \overrightarrow{A}\cdot \overrightarrow{B}=1\end{array}$

Panjang kedua vektor:

∣∣A⃗ ∣∣=12+12‾‾‾‾‾‾‾√∣∣A⃗ ∣∣=1+1‾‾‾‾‾√∣∣A⃗ ∣∣=2‾√∣∣B⃗ ∣∣=02+12‾‾‾‾‾‾‾√∣∣B⃗ ∣∣=0+1‾‾‾‾‾√∣∣B⃗ ∣∣=1‾√=1$\begin{array}{ccc}\begin{array}{l}\left|\overrightarrow{A}\right|=\sqrt{1^2+1^2}\\ \left|\overrightarrow{A}\right|=\sqrt{1+1}\\ \left|\overrightarrow{A}\right|=\sqrt{2}\end{array}& & \begin{array}{l}\left|\overrightarrow{B}\right|=\sqrt{0^2+1^2}\\ \left|\overrightarrow{B}\right|=\sqrt{0+1}\\ \left|\overrightarrow{B}\right|=\sqrt{1}=1\end{array}\end{array}$

Misalkan sudut yang dibentuk oleh kedua vektor tersebut adalah θ, maka:

θ=cos−1(A⃗ ⋅B⃗ ∣∣A⃗ ∣∣∣∣B⃗ ∣∣)θ=cos−1(12√×1)θ=cos−1(12√)rasionalisasipenyebutθ=cos−1(122‾√)θ=45∘$\begin{array}{l}\theta ={\cos }^{-1}\left(\frac{\overrightarrow{A}\cdot \overrightarrow{B}}{\left|\overrightarrow{A}\right|\left|\overrightarrow{B}\right|}\right)\\ \theta ={\cos }^{-1}\left(\frac{1}{\sqrt{2}\times 1}\right)\\ \theta ={\cos }^{-1}\left(\frac{1}{\sqrt{2}}\right)\begin{array}{l}\end{array}\text{rasionalisasi}\begin{array}{l}\end{array}\text{penyebut}\\ \theta ={\cos }^{-1}\left(\frac{1}{2}\sqrt{2}\right)\\ \theta ={45}^{\circ }\end{array}$

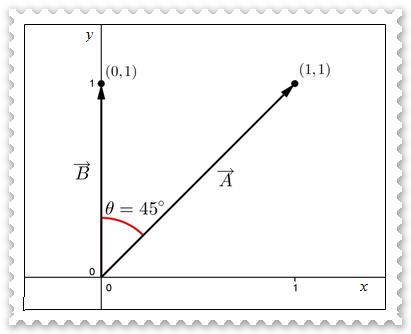
Jadi, besar sudut antara vektor A⃗ =⟨1,1⟩$\overrightarrow{A}=⟨1,1⟩$ dan vektor B⃗ =⟨0,1⟩$\overrightarrow{B}=⟨0,1⟩$ adalah 45°.

Mengingat kedua vektor tersebut berada pada ruang dimensi 2, maka kita masih dapat menggambarkan kedua vektor pada koordinat Cartesius sebagai berikut.

♫ Contoh 2

Tentukan besar sudut antara vektor P⃗ =⟨1,1,1⟩$\overrightarrow{P}=⟨1,1,1⟩$ dan vektor Q⃗ =⟨2,0,2⟩$\overrightarrow{Q}=⟨2,0,2⟩$.

♫ Penyelesaian:

Untuk menentukan besar sudut antara kedua vektor tersebut, terlebih dahulu hitunglah perkalian skalar kedua vektor dan panjang masing-masing vektor.

Perkalian skalar kedua vektor:

P⃗ ⋅Q⃗ =⟨1,1,1⟩⋅⟨2,0,2,⟩P⃗ ⋅Q⃗ =(1×2)+(1×0)+(1×2)P⃗ ⋅Q⃗ =2+0+2P⃗ ⋅Q⃗ =4$\begin{array}{l}\overrightarrow{P}\cdot \overrightarrow{Q}=⟨1,1,1⟩\cdot ⟨2,0,2,⟩\\ \overrightarrow{P}\cdot \overrightarrow{Q}=(1\times 2)+(1\times 0)+(1\times 2)\\ \overrightarrow{P}\cdot \overrightarrow{Q}=2+0+2\\ \overrightarrow{P}\cdot \overrightarrow{Q}=4\end{array}$

Panjang kedua vektor:

∣∣P⃗ ∣∣=12+12+12‾‾‾‾‾‾‾‾‾‾‾‾√∣∣P⃗ ∣∣=1+1+1‾‾‾‾‾‾‾‾‾√∣∣P⃗ ∣∣=3‾√∣∣Q⃗ ∣∣=22+02+22‾‾‾‾‾‾‾‾‾‾‾‾√∣∣Q⃗ ∣∣=4+0+4‾‾‾‾‾‾‾‾‾√∣∣Q⃗ ∣∣=8‾√$\begin{array}{lll}\begin{array}{l}\left|\overrightarrow{P}\right|=\sqrt{1^2+1^2+1^2}\\ \left|\overrightarrow{P}\right|=\sqrt{1+1+1}\\ \left|\overrightarrow{P}\right|=\sqrt{3}\end{array}& & \begin{array}{l}\left|\overrightarrow{Q}\right|=\sqrt{2^2+0^2+2^2}\\ \left|\overrightarrow{Q}\right|=\sqrt{4+0+4}\\ \left|\overrightarrow{Q}\right|=\sqrt{8}\end{array}\end{array}$

Misalkan sudut yang dibentuk oleh kedua vektor tersebut adalah θ, maka:

θ=cos−1(P⃗ ⋅Q⃗ ∣∣P⃗ ∣∣∣∣Q⃗ ∣∣)θ=cos−1(43√×8√)θ=cos−1(424√)menggunakan kalkulatorθ≈35,3∘$\begin{array}{l}\theta ={\cos }^{-1}\left(\frac{\overrightarrow{P}\cdot \overrightarrow{Q}}{\left|\overrightarrow{P}\right|\left|\overrightarrow{Q}\right|}\right)\\ \theta ={\cos }^{-1}\left(\frac{4}{\sqrt{3}\times \sqrt{8}}\right)\\ \theta ={\cos }^{-1}\left(\frac{4}{\sqrt{24}}\right)\begin{array}{l}\end{array}\text{menggunakan kalkulator}\\ \theta \approx 35,3^{\circ }\end{array}$

Jadi, besar sudut antara vektor P⃗ =⟨1,1,1⟩$\overrightarrow{P}=⟨1,1,1⟩$ dan vektor Q⃗ =⟨2,0,2⟩$\overrightarrow{Q}=⟨2,0,2⟩$ adalah 35,3°.

▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩

Catatan:

Dalam beberapa kasus, penggunaan kalkulator saintifik sangat dibutuhkan untuk mempermudah penentuan sudut yang bersesuaian dengan nilai trigonometri yang diberikan. Seperti pada contoh di atas, kita hendak menentukan nilai dari:

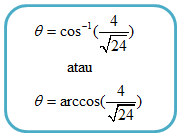
Persamaan di atas dapat diartikan sebagai, “Sudut berapa yang nilai kosinusnya sama dengan 424√$\frac{4}{\sqrt{24}}$.”

Untuk menghitung invers dari kosinus atau fungsi trigonometri lainnya dengan menggunakan kalkulator saintifik, kalian dapat mengikuti langkah-langkah berikut.

𝟙. Aturlah dahulu satuan sudut sesuai dengan permintaan soal, apakah dalam satuan derajat atau radian.

Pada kalkulator saintifik, terdapat beberapa mode satuan sudut. Untuk itu, atur mode kalkulator kalian dalam satuan yang diinginkan.

𝟚. Untuk menghitung nilai invers dari kosinus kita sebelumnya, tekan tombol-tombol dengan urutan sebagai berikut:

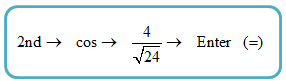
Hasil akhir yang ditampilkan adalah 35,26438968… yang kita bulatkan menjadi 35,3°.

Perlu kalian ketahui bahwa urutan tombol di atas tidak berlaku untuk semua jenis kalkulator saintifik. Jadi, ada baiknya kalian membaca dengan teliti petunjuk penggunaan kalkulator yang kalian miliki sebelum menggunakannya.