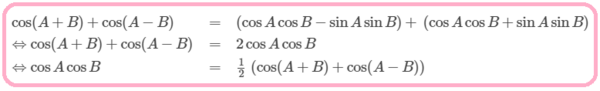Perkalian Sinus dan Kosinus

Perkalian Sinus dan Kosinus - Pada topik sebelumnya kalian telah belajar mengenai jumlah dan selisih sinus dan kosinus dua sudut. Apakah kalian masih ingat dengan materi tersebut?

Ya, ada empat rumus yang perlu kalian ingat kembali terkait jumlah dan selisih sinus dan kosinus dua sudut, yaitu:

1. sin(A+B)=sinAcosB+cosAsinB$\sin (A+B)=\sin A\cos B+\cos A\sin B$
2. sin(A−B)=sinAcosB−cosAsinB$\sin (A-B)=\sin A\cos B-\cos A\sin B$
3. cos(A+B)=cosAcosB−sinAsinB$\cos (A+B)=\cos A\cos B-\sin A\sin B$
4. cos(A−B)=cosAcosB+sinAsinB$\cos (A-B)=\cos A\cos B+\sin A\sin B$

Apa yang dapat kalian simpulkan dari keempat rumus di atas?

Benar sekali. Ruas kanan dari keempat rumus di atas memuat perkalian sinus dan kosinus.

Bentuk perkalian sinus dan kosinus tersebut adalah sinAcosB$\sin A\cos B$ dan cosAsinB$\cos A\sin B$. Adapun bentuk perkalian yang lain adalah cosAcosB$\cos A\cos B$ dan sinAsinB$\sin A\sin B$.

✎ Jika kita jumlahkan rumus 1 dan 2, maka akan kita peroleh hasil sebagai berikut:

✎ Jika kita kurangkan rumus 1 dan 2, maka akan kita peroleh hasil sebagai berikut:

✎ Jika kita jumlahkan rumus 3 dan 4, maka akan kita peroleh hasil sebagai berikut:

✎ Jika kita kurangkan rumus 3 dan 4, maka akan kita peroleh hasil sebagai berikut:

Nah, dari uraian di atas, dapat kita simpulkan bahwa:

• sinAcosB=12[sin(A+B)+sin(A−B)]$\sin A\cos B=\frac{1}{2}\left[\sin \left(A+B\right)+\sin \left(A-B\right)\right]$
• cosAsinB=12[sin(A+B)−sin(A−B)]$\cos A\sin B=\frac{1}{2}\left[\sin \left(A+B\right)-\sin \left(A-B\right)\right]$
• cosAcosB=12[cos(A+B)+cos(A−B)]$\cos A\cos B=\frac{1}{2}\left[\cos \left(A+B\right)+\cos \left(A-B\right)\right]$
• sinAsinB=−12[cos(A+B)−cos(A−B)]$\sin A\sin B=-\frac{1}{2}\left[\cos \left(A+B\right)-\cos \left(A-B\right)\right]$

Apakah kalian sudah paham dengan penjelasan materi di atas?

Yuk kita cermati beberapa contoh berikut agar kalian semakin paham.

Contoh 1

Ubahlah bentuk perkalian berikut ke dalam bentuk penjumlahan atau pengurangan.

• 2sin35ocos15o$2\sin {35}^o\cos {15}^o$
• 8cos64osin24o$8\cos {64}^o\sin {24}^o$
• cos24,5ocos10,5o$\cos 24,5^o\cos 10,5^o$
• 6sin134osin65o$6\sin {134}^o\sin {65}^o$

Penyelesaian:

2sin35ocos15o==2[12(sin(35o+15o)+sin(35o−15o))]sin50o+sin20o$\begin{array}{l}\mathrm{<br>}\end{array}$

$\begin{array}{lll}2\sin {35}^o\cos {15}^o& =& 2\left[\frac{1}{2}\left(\sin ({35}^o+{15}^o)+\sin ({35}^o-{15}^o)\right)\right]\\ & =& \sin {50}^o+\sin {20}^o\end{array}$

8cos64osin24o===8[12(sin(64o+24o)−sin(64o−24o))]4(sin88o−sin40o)4sin88o−4sin40o$\begin{array}{l}\mathrm{<br>}\end{array}$

$\begin{array}{lll}8\cos {64}^o\sin {24}^o& =& 8\left[\frac{1}{2}\left(\sin ({64}^o+{24}^o)-\sin ({64}^o-{24}^o)\right)\right]\\ & =& 4\left(\sin {88}^o-\sin {40}^o\right)\\ & =& 4\sin {88}^o-4\sin {40}^o\end{array}$

cos24,5ocos10,5o===12[cos(24,5o+10,5o)+cos(24,5o−10,5o)]12(cos35o+cos14o)12cos35o+12cos14o$\begin{array}{l}\mathrm{<br>}\end{array}$

$\begin{array}{lll}\cos 24,5^o\cos 10,5^o& =& \frac{1}{2}\left[\cos \left(24,5^o+10,5^o\right)+\cos \left(24,5^o-10,5^o\right)\right]\\ & =& \frac{1}{2}\left(\cos {35}^o+\cos {14}^o\right)\\ & =\end{array}$

$\begin{array}{l}\frac{1}{2}\cos {35}^o+\frac{1}{2}\cos {14}^o\end{array}$

6sin134osin65o===6[−12(cos(134o+65o)−cos(134o−65o))]−3(cos199o+cos69o)−3cos199o−3cos69o$\begin{array}{l}\mathrm{<br>}\end{array}$

$\begin{array}{lll}6\sin {134}^o\sin {65}^o& =& 6\left[-\frac{1}{2}\left(\cos ({134}^o+{65}^o)-\cos ({134}^o-{65}^o)\right)\right]\\ & =\end{array}$

$\begin{array}{l}-3\left(\cos {199}^o+\cos {69}^o\right)\\ & =& -3\cos {199}^o-3\cos {69}^o\end{array}$

Pada contoh 1 di atas, sudut yang diketahui bukanlah sudut istimewa, sehingga untuk menentukan nilai sinus dan kosinus dari sudut tersebut kalian memerlukan kalkulator ataupun tabel sinus dan kosinus. Nah, jika besar sudut merupakan sudut istimewa, kalian dapat langsung menentukan nilainya.

Tentu kalian masih ingat dengan nilai sinus dan kosinus sudut istimewa bukan?

Yuk kita cermati contoh 2 berikut.

Contoh 2

Tentukan hasil perkalian berikut:

• 2sin45ocos15o$2\sin {45}^o\cos {15}^o$
• 2cos45osin15o$2\cos {45}^o\sin {15}^o$
• 4cos15ocos75o$4\cos {15}^o\cos {75}^o$
• 8sin7,5osin37,5o$8\sin 7,5^o\sin 37,5^o$

Penyelesaian:

2sin45ocos15o====2[12(sin(45o+15o)+sin(45o−15o))]sin60o+sin30o123‾√+1212(3‾√+1)$\begin{array}{l}\mathrm{<br>}\end{array}$

$\begin{array}{lll}2\sin {45}^o\cos {15}^o& =& 2\left[\frac{1}{2}\left(\sin ({45}^o+{15}^o)+\sin ({45}^o-{15}^o)\right)\right]\\ & =& \sin {60}^o+\sin {30}^o\\ & =& \frac{1}{2}\sqrt{3}+\frac{1}{2}\\ & =& \frac{1}{2}\left(\sqrt{3}+1\right)\end{array}$

2cos45osin15o====2[12(sin(45o+15o)−sin(45o−15o))]sin60o−sin30o123‾√−1212(3‾√−1)$\begin{array}{l}\mathrm{<br>}\end{array}$

$\begin{array}{lll}2\cos {45}^o\sin {15}^o& =& 2\left[\frac{1}{2}\left(\sin ({45}^o+{15}^o)-\sin ({45}^o-{15}^o)\right)\right]\\ & =& \sin {60}^o-\sin {30}^o\\ & =& \frac{1}{2}\sqrt{3}-\frac{1}{2}\\ & =& \frac{1}{2}\left(\sqrt{3}-1\right)\end{array}$

4cos15ocos75o=====4[12(cos(15o+75o)+cos(15o−75o))]2(cos90o+cos(−60o))2(cos90o+cos60o)2(0−12)−1$\begin{array}{l}\mathrm{<br>}\end{array}$

$\begin{array}{lll}4\cos {15}^o\cos {75}^o& =& 4\left[\frac{1}{2}\left(\cos ({15}^o+{75}^o)+\cos ({15}^o-{75}^o)\right)\right]\\ & =& 2\left(\cos {90}^o+\cos \left(-{60}^o\right)\right)\\ & =& 2\end{array}$

$\begin{array}{l}\left(\cos {90}^o+\cos {60}^o\right)\\ & =& 2\left(0-\frac{1}{2}\right)\\ & =& -1\end{array}$

8sin7,5osin37,5o=====8[−12(cos(7,5o+37,5o)−cos(7,5o−37,5o))]−4(cos45o−cos(−30o))−4(cos45o−cos30o)−4(122‾√−123‾√)2(3‾√−2‾√)
$\begin{array}{l}\mathrm{<br>}\end{array}$

$\begin{array}{lll}8\sin 7,5^o\sin 37,5^o& =& 8\left[-\frac{1}{2}\left(\cos (7,5^o+37,5^o)-\cos (7,5^o-37,5^o)\right)\right]\\ & =& -4\left(\cos {45}^o-\cos \left(-{30}^o\right)\right)\\ & =& -4\end{array}$

$\begin{array}{l}\left(\cos {45}^o-\cos {30}^o\right)\\ & =& -4\left(\frac{1}{2}\sqrt{2}-\frac{1}{2}\sqrt{3}\right)\\ & =& 2\left(\sqrt{3}-\sqrt{2}\right)\end{array}$

Yuk uji pemahaman kalian dengan mengerjakan sepuluh soal latihan dalam topik ini.