Jumlah dan Selisih Sinus

Jumlah dan Selisih Sinus - Jika pada topik sebelumnya kalian telah belajar tentang rumus sinus jumlah dan selisih dua sudut, pada topik ini kalian akan belajar tentang rumus jumlah dan selisih sinus. Adakah hubungan dari kedua rumus tersebut? Untuk tahu jawabannya, mari simak uraian berikut.

Apakah kalian masih ingat dengan bentuk sin (α + β) dan sin (α - β)? Ya, bentuk tersebut adalah sinus jumlah dan selisih dua sudut. Sebelum mempelajari topik ini, kalian sudah harus menguasai bentuk yang setara dari keduanya. Oleh karena itu, mari kita ingat kembali.

                                          

       Misalkan α dan β adalah sebuah sudut. Jumlah dan selisih sinus dari kedua sudut tersebut dapat dinyatakan dengan sin α + sin β dan sin α - sin β. Bentuk yang setara dari keduanya dinamakan dengan rumus jumlah dan selisih sinus. Bagaimana cara menentukan rumusnya? Mari kita pelajari bersama.

► Bentuk Jumlah dan Selisih dari Rumus Sinus Jumlah dan Selisih Dua Sudut ◄

Untuk menentukan rumus jumlah dan selisih sinus, lakukan dahulu penjumlahan dan pengurangan pada rumus sinus jumlah dan selisih dua sudut seperti berikut.

Penjumlahan rumus sinus jumlah dan selisih dua sudut:

sin(α+β)=sinαcosβ+cosαsinβsin(α−β)=sinαcosβ−cosαsinβsin(α+β)+sin(α−β)=2sinαcosβ...(i)+$\frac{\begin{array}{l}\sin (\alpha +\beta )=\sin \alpha \cos \beta +\cos \alpha \sin \beta \\ \sin (\alpha -\beta )\end{array}}{}$

$\frac{\begin{array}{l}=\sin \alpha \cos \beta -\cos \alpha \sin \beta \end{array}}{\sin (\alpha +\beta )+\sin (\alpha -\beta )=2\sin \alpha \cos \beta ...(\mathrm{i})}+$

Pengurangan rumus sinus jumlah dan selisih dua sudut:

sin(α+β)=sinαcosβ+cosαsinβsin(α−β)=sinαcosβ−cosαsinβsin(α+β)−sin(α−β)=2cosαsinβ...(ii)−$\frac{\begin{array}{l}\sin (\alpha +\beta )=\sin \alpha \cos \beta +\cos \alpha \sin \beta \\ \sin (\alpha -\beta )\end{array}}{}$

$\frac{\begin{array}{l}=\sin \alpha \cos \beta -\cos \alpha \sin \beta \end{array}}{\sin (\alpha +\beta )-\sin (\alpha -\beta )=2\cos \alpha \sin \beta ...(\mathrm{i}\mathrm{i})}-$

Dari persamaan (i) dan (ii) inilah rumus jumlah dan selisih sinus dapat ditentukan.

► Rumus jumlah dan selisih sinus ◄

Dari pembahasan sebelumnya, diperoleh:

sin (α + β) + sin (α - β) = 2 sin α cos β ... (i)

sin (α + β) - sin (α - β) = 2 cos α sin β ... (ii)

Misalkan x = α + β dan y = α - β. Dengan menjumlahkan kedua pemisalan ini, kita peroleh:

x=α+βy=α−βx+y=2α+$\frac{\begin{array}{l}x=\alpha +\beta \\ y=\alpha -\beta \end{array}}{x+y=2\alpha }+$

dengan kata lain, kita peroleh α=12(x+y)$\alpha =\frac{1}{2}(x+y)$ .

Selanjutnya, dengan mengurangkan kedua pemisalan tersebut, kita peroleh:

x=α+βy=α−βx−y=2β−$\frac{\begin{array}{l}x=\alpha +\beta \\ y=\alpha -\beta \end{array}}{x-y=2\beta }-$

dengan kata lain, kita peroleh β=12(x−y)$\beta =\frac{1}{2}(x-y)$.

Sekarang, substitusikan nilai α dan β ke persamaan (i) dan (ii).

Persamaan (i)

sin(α+β)+sin(α−β)=2sinαcosβ⇔sinx+siny=2sin12(x+y)cos12(x−y)$\begin{array}{l}\mathrm{<br>}\end{array}$

$\begin{array}{l}\sin (\alpha +\beta )+\sin (\alpha -\beta )=2\sin \alpha \cos \beta \\ \iff \sin x+\sin y=2\sin \frac{1}{2}(x+y)\cos \frac{1}{2}(x-y)\end{array}$

Persamaan (ii)

sin(α+β)−sin(α−β)=2cosαsinβ⇔sinx−siny=2cos12(x+y)sin12(x−y)$\begin{array}{l}\mathrm{<br>}\end{array}$

$\begin{array}{l}\sin (\alpha +\beta )-\sin (\alpha -\beta )=2\cos \alpha \sin \beta \\ \iff \sin x-\sin y=2\cos \frac{1}{2}(x+y)\sin \frac{1}{2}(x-y)\end{array}$

Dari hasil substitusi di atas, kita dapatkan rumus jumlah dan selisih sinus sebagai berikut.

sinx+siny=2sin12(x+y)cos12(x−y)sinx−siny=2cos12(x+y)sin12(x−y)$\begin{array}{l}\mathrm{<br>}\end{array}$

$\begin{array}{l}\sin x+\sin y=2\sin \frac{1}{2}(x+y)\cos \frac{1}{2}(x-y)\\ \sin x-\sin y=2\cos \frac{1}{2}(x+y)\sin \frac{1}{2}(x-y)\end{array}$

Perhatikan bahwa x, y, α, dan β adalah variabel yang dapat kita ganti dengan simbol apa saja. Dengan demikian, rumus jumlah dan selisih sinus dapat kita nyatakan ulang sebagai berikut.

                               

Rumus ini terkesan rumit, namun perhatikan bahwa hanya terjadi perubahan posisi fungsi sinus dan kosinus saat kita menjumlahkan atau mengurangkannya. Untuk menghafal dengan mudah kedua rumus ini, kita dapat memanfaatkan jembatan keledai berikut.

            

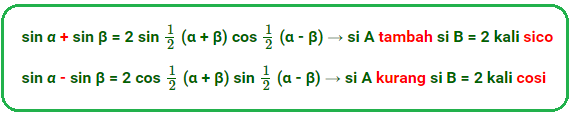
Kalian dapat membuat sendiri jembatan keledai yang kalian anggap lebih mudah untuk diingat. Ayo kalian coba.

Contoh 1

Jika α = 75° dan β = 15°, maka nilai dari sin α + sin β adalah ....

Penyelesaian:

Berdasarkan rumus jumlah sinus dengan nilai α = 75° dan β = 15°, diperoleh:

sinα+sinβ=2sin12(α+β)cos12(α−β)⇔sin75∘+sin15∘=2sin12(75∘+15∘)cos12(75∘−15∘)⇔sin75∘+sin15∘=2sin1290∘cos12(60∘)⇔sin75∘+sin15∘=2sin45∘cos30∘⇔sin75∘+sin15∘=2(122‾√)(123‾√)⇔sin75∘+sin15∘=126‾√$\begin{array}{l}\mathrm{<br>}\end{array}$

$\begin{array}{l}\sin \alpha +\sin \beta =2\sin \frac{1}{2}(\alpha +\beta )\cos \frac{1}{2}(\alpha -\beta )\\ \iff \sin {75}^{\circ }+\sin {15}^{\circ }=2\sin \frac{1}{2}({75}^{\circ }+{15}^{\circ })\cos \frac{1}{2}({75}^{\circ }-{15}^{\circ })\end{array}$

$\begin{array}{l}\iff \sin {75}^{\circ }+\sin {15}^{\circ }=2\sin \frac{1}{2}{90}^{\circ }\cos \frac{1}{2}({60}^{\circ })\\ \iff \sin {75}^{\circ }+\sin {15}^{\circ }=2\sin {45}^{\circ }\cos {30}^{\circ }\\ \iff \sin {75}^{\circ }+\sin {15}^{\circ }\end{array}$

$\begin{array}{l}=2(\frac{1}{2}\sqrt{2})(\frac{1}{2}\sqrt{3})\\ \iff \sin {75}^{\circ }+\sin {15}^{\circ }=\frac{1}{2}\sqrt{6}\end{array}$

Jadi, nilai dari sin 75° + sin 15° adalah 126‾√$\frac{1}{2}\sqrt{6}$.

Contoh 2

Bentuk perkalian dari sin 5x - sin x adalah ….

Penyelesaian:

Berdasarkan rumus selisih sinus dengan nilai α = 5x dan β = x, diperoleh:

sinα−sinβ=2cos12(α+β)sin12(α−β)⇔sin5x−sinx=2cos12(5x+x)sin12(5x−x)⇔sin5x−sinx=2cos12(6x)sin12(4x)⇔sin5x−sinx=2cos3xsin2x$\begin{array}{l}\mathrm{<br>}\end{array}$

$\begin{array}{l}\sin \alpha -\sin \beta =2\cos \frac{1}{2}(\alpha +\beta )\sin \frac{1}{2}(\alpha -\beta )\\ \iff \sin 5x-\sin x=2\cos \frac{1}{2}(5x+x)\sin \frac{1}{2}(5x-x)\end{array}$

$\begin{array}{l}\iff \sin 5x-\sin x=2\cos \frac{1}{2}(6x)\sin \frac{1}{2}(4x)\\ \iff \sin 5x-\sin x=2\cos 3x\sin 2x\end{array}$

Jadi, bentuk perkalian dari sin 5x - sin x adalah 2 cos 3x sin 2x.

Contoh 3

Perhatikan segitiga siku-siku ABC berikut ini.

                                          

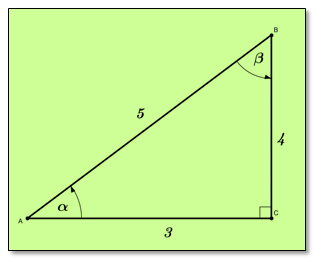
Berdasarkan gambar tersebut, nilai dari cos12(α+β)sin12(α−β)$\cos \frac{1}{2}(\alpha +\beta )\sin \frac{1}{2}(\alpha -\beta )$ adalah….

Penyelesaian:

Oleh karena 2cos12(α+β)sin12(α−β)=sinα−sinβ$2\cos \frac{1}{2}(\alpha +\beta )\sin \frac{1}{2}(\alpha -\beta )=\sin \alpha -\sin \beta$, maka:

cos12(α+β)sin12(α−β)=sinα−sinβ2$\cos \frac{1}{2}(\alpha +\beta )\sin \frac{1}{2}(\alpha -\beta )=\frac{\sin \alpha -\sin \beta }{2}$ .

Dari segitiga siku-siku ABC di atas, dapat diketahui:

sinα=panjangsisididepansudutαpanjangsisimiring=45$\sin \alpha =\frac{\mathrm{p}\mathrm{a}\mathrm{n}\mathrm{j}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{s}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{d}\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{p}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{u}\mathrm{d}\mathrm{u}\mathrm{t}\alpha }{\mathrm{p}\mathrm{a}\mathrm{n}\mathrm{j}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{s}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{r}\mathrm{i}\mathrm{n}\mathrm{g}}=\frac{4}{5}$

sinβ=panjangsisididepansudutβpanjangsisimiring=35$\sin \beta =\frac{\mathrm{p}\mathrm{a}\mathrm{n}\mathrm{j}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{s}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{d}\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{p}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{u}\mathrm{d}\mathrm{u}\mathrm{t}\beta }{\mathrm{p}\mathrm{a}\mathrm{n}\mathrm{j}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{s}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{r}\mathrm{i}\mathrm{n}\mathrm{g}}=\frac{3}{5}$

Dengan demikian, diperoleh:

cos12(α+β)sin12(α−β)=sinα−sinβ2⇔cos12(α+β)sin12(α−β)=45−352⇔cos12(α+β)sin12(α−β)=152⇔cos12(α+β)sin12(α−β)=110$\begin{array}{l}\mathrm{<br>}\end{array}$

$\begin{array}{l}\mathrm{<br>}\end{array}$

$\begin{array}{l}\cos \frac{1}{2}(\alpha +\beta )\sin \frac{1}{2}(\alpha -\beta )=\frac{\sin \alpha -\sin \beta }{2}\\ \iff \cos \frac{1}{2}(\alpha +\beta )\sin \frac{1}{2}(\alpha -\beta )=\frac{\frac{4}{5}-\frac{3}{5}}{2}\\ \iff \cos \frac{1}{2}\end{array}$

$\begin{array}{l}(\alpha +\beta )\sin \frac{1}{2}(\alpha -\beta )=\frac{\frac{1}{5}}{2}\\ \iff \cos \frac{1}{2}(\alpha +\beta )\sin \frac{1}{2}(\alpha -\beta )=\frac{1}{10}\end{array}$

Jadi, nilai dari cos12(α+β)sin12(α−β)$\cos \frac{1}{2}(\alpha +\beta )\sin \frac{1}{2}(\alpha -\beta )$ adalah 110$\frac{1}{10}$.

Poin Penting

1. Rumus jumlah dan selisih sinus dapat diperoleh dari penjumlahan dan pengurangan rumus sinus jumlah dan selisih dua sudut dengan pemisalan tertentu.

sin(α+β)+sin(α−β)=2sinαcosβ$\sin (\alpha +\beta )+\sin (\alpha -\beta )=2\sin \alpha \cos \beta$

sin(α+β)−sin(α−β)=2cosαsinβ$\sin (\alpha +\beta )-\sin (\alpha -\beta )=2\cos \alpha \sin \beta$

2. Rumus jumlah dan selisih sinus adalah sebagai berikut.

sinα+sinβ=2sin12(α+β)cos12(α−β)sinα−sinβ=2cos12(α+β)sin12(α−β)$\begin{array}{r}\mathrm{s}\mathrm{i}\mathrm{n}\alpha +\mathrm{s}\mathrm{i}\mathrm{n}\beta =2\mathrm{s}\mathrm{i}\mathrm{n}\frac{1}{2}(\alpha +\beta )\mathrm{c}\mathrm{o}\mathrm{s}\frac{1}{2}(\alpha -\beta )\\ \mathrm{s}\mathrm{i}\mathrm{n}\alpha -\mathrm{s}\mathrm{i}\mathrm{n}\beta =2\mathrm{c}\mathrm{o}\mathrm{s}\frac{1}{2}(\alpha +\beta )\mathrm{s}\mathrm{i}\mathrm{n}\frac{1}{2}(\alpha -\beta )\end{array}$

Apakah kalian sudah paham dengan penjelasan di atas? Agar pemahaman kalian bertambah lagi, yuk kerjakan latihan soal-soal berikut ini.