Penjumlahan dan Selisih Kosinus Dua Sudut

Penjumlahan dan Selisih Kosinus Dua Sudut - Sekitar 9 abad yang lalu yaitu pada abad ke-12 Masehi, Bhaskara II seorang matematikawan India membuat kemajuan besar dalam perkembangan ilmu navigasi dan astronomi dengan penemuan rumus kosinus dan sinus untuk jumlah dan selisih dua sudut. Penemuan rumus ini memungkinkan para ahli perbintangan dan navigasi untuk melakukan perhitungan dengan ketelitian dan efisiensi yang lebih tinggi dari sebelumnya. 

Pada topik ini, kamu akan mempelajari salah satu rumus yang ditemukan Bhaskara yaitu rumus kosinus jumlah dan selisih sudut. Rumus ini sangat bermanfaat untuk menghitung nilai dari kosinus atau sinus sudut tak istimewa.

       Mari kita ingat kembali tentang lawan dari sudut tak istimewa yaitu sudut istimewa.Tabel berikut ini merangkum beberapa sudut istimewa beserta nilai perbandingan trigonometrinya.

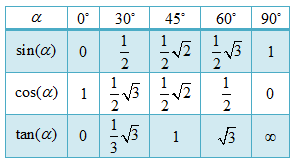
Sudut istimewa lainnya merupakan kelipatan bulat dari sudut-sudut di atas, sedangkan sudut tak istimewa dapat dipahami sebagai sudut-sudut selain sudut istimewa misalkan 15⁰, 41⁰, 88⁰, dan lain-lain.

Konsep yang Mendasari Kosinus Jumlah dan Selisih Sudut

Definisi dasar fungsi trigonometri dan konsep jarak dua titik perlu kamu ingat kembali untuk memahami pembuktian rumus kosinus jumlah dan selisih dua sudut

Definisi Dasar Fungsi Trigonometri

Perhatikan segitiga siku-siku ABC berikut.

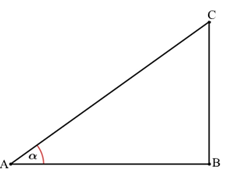
Pada segitiga siku-siku ABC berlaku definisi dasar fungsi trigonometri antara lain:

sinα=BCAC→BC=ACsinα$\sin \alpha =\frac{BC}{AC}\to BC=AC\sin \alpha$
cosα=ABAC→AB=ACcosα$\cos \alpha =\frac{AB}{AC}\to AB=AC\cos \alpha$
tanα=BCAB→BC=ABtanα$\tan \alpha =\frac{BC}{AB}\to BC=AB\tan \alpha$

sin2α+cos2α=1${\sin }^2\alpha +{\cos }^2\alpha =1$

Jarak Dua Titik

Perhatikan gambar di bawah ini.

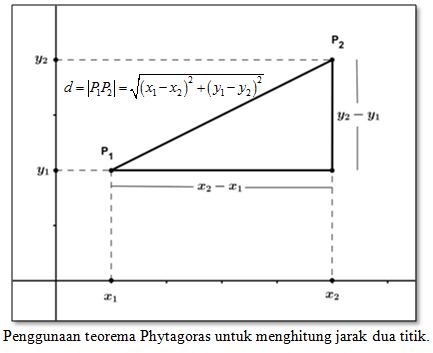
Pada gambar di atas terdapat dua titik yaitu P1(x1, y1) dan P2(x2, y2), sehingga jarak antara kedua titik ini dinyatakan sebagai:

d=|P1P2|=(x1−x2)2+(y1−y2)2‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾√$d=\left|P_1{P}_2\right|=\sqrt{{(x_1-x_2)}^2+{(y_1-y_2)}^2}$

Pembuktian Rumus Kosinus Jumlah dan Selisih Sudut

Untuk tiap sudut α dan β baik itu dalam satuan derajat maupun radian berlaku rumus kosinus jumlah dan selisih kedua sudut tersebut yaitu:

cos (α - β) = cos α . cos α + sin α . sin β

cos (α + β) = cos α . cos α - sin α . sin β

Bentuk terakhir diruas kanan dapat disederhanakan menjadi:

⇔d2=|AB|2=2−2cosαcosβ−2sinαsinβ$\iff d^2={\left|AB\right|}^2=2-2\cos \alpha \cos \beta -2\sin \alpha \sin \beta$

Titik A, O, dan B dihubungkan sehingga terbentuk ∆AOB.

Selanjutnya, putar (rotasikan) ∆AOB (segitiga dalam lingkaran satuan di atas) searah jarum jam dengan pusat O (0, 0) sebesar β sehingga diperoleh segitiga kongruen A’OB’ yang berhimpit dengan sumbu x positif seperti gambar di bawah ini.

Oleh karena ∆AOB diputar dengan pusat O (0, 0) searah jarum jam sebesar β, maka setiap sudut yang terbentuk ditambah dengan (-β).

Koordinat baru untuk kedua titik A dan B masing-masing berupa A’ dan B’, yaitu:

A′(a′x,a′y)=A′(1,0)$A^{\prime }\left(a_x^{\prime },a_y^{\prime }\right)=A^{\prime }\left(1,0\right)$
B′(b′x,b′y)=B′(cos(α−β),sin(α−β))$B^{\prime }\left(b_x^{\prime },b_y^{\prime }\right)=B^{\prime }\left(\cos \left(\alpha -\beta \right),\sin \left(\alpha -\beta \right)\right)$

Oleh karena rotasi hanya merubah posisi dan tidak mengubah bentuk serta ukuran bangun datar, maka ∆AOB dan ∆A’OB’ merupakan segitiga yang kongruen.

Oleh karena kedua segitiga tersebut kongruen, maka diperoleh d2 = d’2 , sehingga:

Jadi, dapat disimpulkan bahwa rumus kosinus selisih sudut adalah:

cos (α - β) = cos α . cos β + sin α . sin β

Untuk membuktikan rumus kosinus jumlah dua sudut, ada 2 hal penting yang harus kamu ketahui.

• cos (-β) = cos β

Perhatikan gambar di bawah ini.

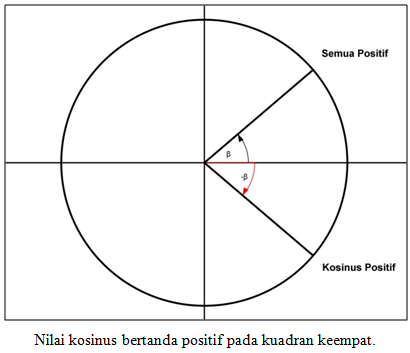
Gambar tersebut menunjukkan, sudut positif (β) berada pada kuadran pertama, sedangkan sudut negatif (-β) terletak pada kuadran keempat. Pada kuadran pertama semua perbandingan trigonometri bertanda positif, sedangkan di kuadran keempat hanya kosinus dan sekan yang bertanda positif, sehingga cos (-β) = cos β.

• sin (-β) = -sin β

Oleh karena hanya kosinus yang bertanda positif di kuadran keempat, maka sinus bertanda negatif, sehingga sin (-β) = -sin β.

Untuk membuktikan rumus kosinus jumlah dua sudut, kita gunakan rumus yang telah kita buktikan sebelumnya yaitu cos (α - β) = cos α . cos β + sin α . sin β dengan mengganti β menjadi -β.

cos(α−(−β))=cosαcos(−β)+sinαsin(−β)$\cos (\alpha -(-\beta ))=\cos \alpha \cos (-\beta )+\sin \alpha \sin (-\beta )$
⇔cos(α+β)=cosαcosβ+sinα(−sinβ)$\iff \cos (\alpha +\beta )=\cos \alpha \cos \beta +\sin \alpha (-\sin \beta )$
⇔cos(α+β)=cosαcosβ−sinαsinβ$\iff \cos (\alpha +\beta )=\cos \alpha \cos \beta -\sin \alpha \sin \beta$

Jadi, dapat simpulkan bahwa rumus kosinus jumlah sudut yaitu:

cos (α + β) = cos α . cos β − sin α . sin β

Agar kamu lebih paham penggunaan rumus kosinus jumlah dan selisih sudut, mari pelajari contoh soal berikut.

◙ ◙ ◙ Contoh 1 ◙ ◙ ◙

Hitunglah nilai dari cos 15⁰.

Penyelesaian:

cos 15⁰ dapat ditulis ulang menggunakan selisih dua sudut istimewa yaitu:

cos 15⁰ = cos (45⁰ - 30⁰)

Dengan menggunakan rumus kosinus selisih sudut yaitu cos (α − β) = cos α . cos β + sinα . sin β dengan α = 45⁰ dan β = 30⁰, maka diperoleh:

◙ ◙ ◙ Contoh 2 ◙ ◙ ◙

Tentukan nilai dari cos 15⁰ . cos 30⁰ - sin 15⁰ . sin 30⁰.

Penyelesaian:

Perhatikan kembali bentuk cos (α + β) = cos α . cos β - sin α . sin β.

Dengan mengganti α = 15⁰ dan β = cos 30⁰, diperoleh:

cos 15⁰ . cos 30⁰ - sin 15⁰ . cos 30⁰ = cos (15⁰ + 30⁰) = cos 45⁰ = 122‾√$\frac{1}{2}\sqrt{2}$

◙ ◙ ◙ Contoh 3 ◙ ◙ ◙

Jika α dan β merupakan sudut lancip dengan sinα=35$\sin \alpha =\frac{3}{5}$ serta cosβ=1213$\cos \beta =\frac{12}{13}$, maka tentukan nilai dari cos(α+β)$\cos (\alpha +\beta )$.

Penyelesaian:

Diketahui:
α dan β merupakan sudut lancip (berada di kuadran 1)
sinα=35$\sin \alpha =\frac{3}{5}$
cosβ=1213$\cos \beta =\frac{12}{13}$

Rumus yang digunakan adalah cos (α + β) = cos α . cos β - sin α . sin β.

Oleh karena cos α dan sin β belum diketahui, maka tentukan nilainya dengan rumus identitas sin2 α + cos2 α = 1.

Untuk cos α
cos2α=1−sin2α${\cos }^2\alpha =1-{\sin }^2\alpha$
⇔cos2α=1−(35)2$\iff {\cos }^2\alpha =1-{\left(\frac{3}{5}\right)}^2$
⇔cos2α=1−925$\iff {\cos }^2\alpha =1-\frac{9}{25}$
⇔cos2α=1625$\iff {\cos }^2\alpha =\frac{16}{25}$
⇔cosα=1625‾‾‾√=45$\iff \cos \alpha =\sqrt{\frac{16}{25}}=\frac{4}{5}$

Untuk sin β
sin2β=1−cos2β${\sin }^2\beta =1-{\cos }^2\beta$
⇔sin2β=1−(1213)2$\iff {\sin }^2\beta =1-{\left(\frac{12}{13}\right)}^2$
⇔sin2β=1−144169$\iff {\sin }^2\beta =1-\frac{144}{169}$
⇔sin2β=25169$\iff {\sin }^2\beta =\frac{25}{169}$
⇔sinβ=25169‾‾‾‾√=513$\iff \sin \beta =\sqrt{\frac{25}{169}}=\frac{5}{13}$

Substitusi nilai sinα=35,cosβ=1213,cosα=45$\sin \alpha =\frac{3}{5},\cos \beta =\frac{12}{13},\cos \alpha =\frac{4}{5}$, dan sinβ=513$\sin \beta =\frac{5}{13}$ ke rumus kosinus jumlah sudut, sehingga:

cos(α+β)=cosαcosβ−sinαsinβ$\cos (\alpha +\beta )=\cos \alpha \cos \beta -\sin \alpha \sin \beta$
⇔cos(α+β)=(45)(1213)−(35)(513)$\iff \cos (\alpha +\beta )=\left(\frac{4}{5}\right)\left(\frac{12}{13}\right)-\left(\frac{3}{5}\right)\left(\frac{5}{13}\right)$
⇔cos(α+β)=4865−1565=3365$\iff \cos (\alpha +\beta )=\frac{48}{65}-\frac{15}{65}=\frac{33}{65}$

◙ ◙ ◙ Contoh 4 ◙ ◙ ◙

Tentukan bentuk paling sederhana dari cos(π2+x)$\cos (\frac{\pi }{2}+x)$ adalah….

Penyelesaian:

Ingat bahwa: π rad = 180⁰ → π2$\frac{\pi }{2}$ rad = 90⁰.

Uraikan bentuk cos(π2+x)$\cos (\frac{\pi }{2}+x)$, sehingga diperoleh:

cos(π2+x)=cosπ2cosx−sinπ2sinx$\cos \left(\frac{\pi }{2}+x\right)=\cos \frac{\pi }{2}\cos x-\sin \frac{\pi }{2}\sin x$
⇔cos(π2+x)=0.cosx−1.sinx$\iff \cos \left(\frac{\pi }{2}+x\right)=0.\cos x-1.\sin x$
⇔cos(π2+x)=0−sinx$\iff \cos \left(\frac{\pi }{2}+x\right)=0-\sin x$
⇔cos(π2+x)=−sinx$\iff \cos \left(\frac{\pi }{2}+x\right)=-\sin x$

Apakah kamu sudah paham dengan penjelasan di atas? Ayo tingkatkan pemahamanmu dengan mengerjakan soal-soal latihan berikut. Selamat belajar.