Penjumlahan dan Selisih Sinus Dua Sudut

Penjumlahan dan Selisih Sinus Dua Sudut - Pernahkan kamu mengamati seorang tukang bangunan yang membangun sebuah rumah? Jika belum, paling tidak kamu dapat membayangkan secara garis besar bagaimana sebuah rumah dibangun. Hal pertama yang dikerjakan saat membangun rumah adalah membuat pondasi dari rumah tersebut. Kemudian, secara bertahap membangun konstruksi lain mulai dari lantai sampai atap. Dalam matematika, khususnya pada pengembangan konsep rumus sinus jumlah dan selisih dua sudut, kita juga menggunakan prinsip yang sama seperti halnya membangun sebuah rumah. Kita akan menggunakan rumus kosinus jumlah dan selisih dua sudut yang telah kita peroleh pada topik sebelumnya, yaitu cos (α ± β) = cos α cos β ∓ sin α sin β sebagai dasar atau pondasi untuk memperoleh rumus sinus jumlah dan selisih dua sudut. Bagaimana caranya? Mari kita pelajari bersama.

Sebelum mempelajari tentang rumus sinus jumlah dan selisih dua sudut, kamu harus memahami tentang sudut-sudut istimewa yang telah diuraikan pada topik sebelumnya. Kamu juga harus mengingat kembali tentang nilai trigonometri di berbagai kuadran. Pemahaman pada konsep tersebut akan sangat berguna untuk memahami konsep-konsep dalam topik ini dan topik-topik selanjutnya. Oleh karena itu, mari simak dengan saksama mengenai nilai trigonometri di berbagai kuadran berikut ini.

●●● Nilai Trigonometri di Berbagai Kuadran ●●●

Tanda nilai untuk sinus, kosinus, dan tangen bervariasi tergantung pada letak kuadrannya. Misalnya, pada kuadran pertama semua nilai trigonometri tersebut bernilai positif (+). Pada kuadran kedua, hanya sinus yang bernilai positif (+), dan sebagainya. Untuk memudahkan kamu dalam mengingat konsep ini, perhatikan gambar berikut.

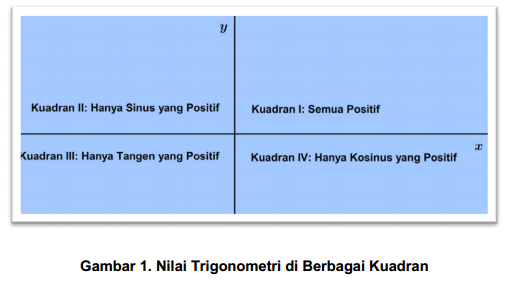
• Pada kuadran I (0⁰ ≤ α ≤ 90⁰), semua nilai trigonometri bernilai positif
• Pada kuadran II (90⁰ ≤ α ≤ 180⁰), hanya sinus yang bernilai positif
• Pada kuadran III (180⁰ ≤ α ≤ 270⁰), hanya tangen yang bernilai positif
• Pada kuadran IV (270⁰ ≤ α ≤ 90⁰), hanya kosinus yang bernilai positif

●●● Rumus Sinus Jumlah dan Selisih Dua Sudut ●●●

Untuk memperoleh rumus sinus jumlah dua sudut, mula-mula perhatikan sebuah lingkaran dengan jari-jari satu satuan atau yang disebut dengan lingkaran satuan berikut ini.

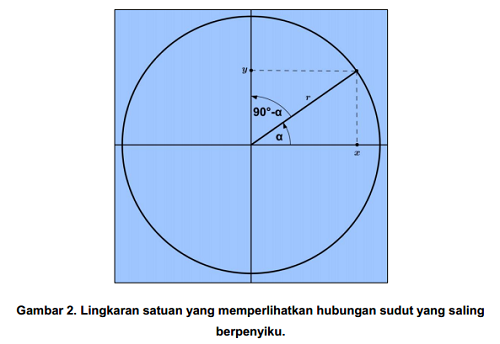
Dengan menerapkan definisi dasar fungsi trigonometri pada gambar 2, dapat kita peroleh beberapa rumus trigonometri berikut:

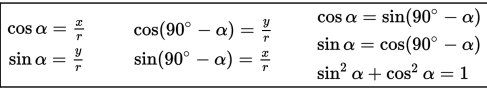
Rumus-rumus tersebut akan kita gunakan untuk memperoleh rumus sinus jumlah dua sudut. Selain itu, kita juga akan menggunakan rumus kosinus selisih dua sudut yang telah kita pelajari pada topik sebelumnya, yaitu:

cos (α – β) = cos α cos β + sin α sin β

Berdasarkan rumus sudut berelasi sin α = cos (90⁰ - α), dapat diketahui bahwa:

sin (α + β) = cos (90⁰ - (α + β))

Perhatikan bahwa:

cos (90⁰ - (α + β)) = cos ((90⁰ - α) - β)

Dengan memanfaatkan rumus kosinus selisih dua sudut, kita dapat jabarkan suku pada ruas kanan menjadi:

cos ((90⁰ - α) - β) = cos (90⁰ - α) cos β + sin (90⁰ - α) sin β

Berdasarkan informasi yang kita peroleh dari gambar 2, dapat kita simpulkan bahwa:

cos ((90⁰ - α) - β) = yr$\frac{y}{r}$ cos β + xr$\frac{x}{r}$ sin β

cos ((90⁰ - α) - β) = sin α cos β + cos α sin β

sin (α + β) = sin α cos β + cos α sin β

Jadi, kita peroleh rumus sinus jumlah dua sudut adalah:

sin (α + β) = sin α cos β + cos α sin β

Untuk memperoleh rumus sinus selisih dua sudut, kita cukup mengganti nilai βmenjadi –β pada rumus sinus jumlah dua sudut yang telah kita peroleh.

sin (α + β) = sin α cos β + cos α sin β

Oleh karena β = - β, maka:

sin (α + (-β)) = sin α cos (-β) + cos α sin (-β)

Sudut β berada pada kuadran pertama, sedangkan sudut -β terletak pada kuadran keempat. Pada kuadran pertama semua perbandingan trigonometri bernilai positif, sedangkan pada kuadran keempat hanya kosinus bernilai positif, sehingga cos (-β) = cos β. Oleh karena hanya kosinus yang bertanda positif di kuadran keempat, maka sinus bertanda negatif, sehingga sin (-β) = -sin β. Dengan demikian, persamaan di atas dapat kita tulis ulang menjadi:

sin (α + (-β)) = sin α cos (-β) + cos α sin (-β)

sin (α - β) = sin α cos β - cos α sin β

Jadi, kita peroleh rumus sinus selisih dua sudut adalah:

sin (α - β) = sin α cos β - cos α sin β

Dari uraian di atas, dapat kita simpulkan bahwa:

sin (α + β) = sin α cos β + cos α sin β

sin (α - β) = sin α cos β - cos α sin β

Keterangan: sudut α dan β dapat dinyatakan dalam satuan derajat ataupun radian (1 πrad = 180⁰).

Nah, setelah kamu mengetahui rumus sinus jumlah dan selisih dua sudut, sekarang saatnya kamu mempelajari penggunaan rumus tersebut dalam perhitungan melalui contoh-contoh berikut.

Contoh 1

Hitunglah nilai dari sin 15⁰.

●●● Penyelesaian: ●●●

sin 15⁰ dapat kita tulis ulang menggunakan sudut istimewa yaitu:

sin 15⁰ = sin (45⁰ - 30⁰)

Dengan menggunakan rumus sinus selisih dua sudut yaitu sin (α - β) = sin α cos β - cosα sin β dengan α = 45⁰ dan β = 30⁰, diperoleh:

sin 15⁰ = sin (45⁰ - 30⁰) = sin 45⁰ cos 30⁰ - cos 45⁰ sin 30⁰

Oleh karena sin 45⁰ = cos 45⁰ = 122‾√$\frac{1}{2}\sqrt{2}$, cos 30⁰ = 123‾√$\frac{1}{2}\sqrt{3}$, dan sin 30⁰ = 12$\frac{1}{2}$, maka:

Jadi, nilai sin 15⁰ =6√−2√4$\frac{\sqrt{6}-\sqrt{2}}{4}$.

Contoh 2

Tentukan nilai dari sin 75⁰ cos 30⁰ - cos 75⁰ sin 30⁰ .

●●● Penyelesaian: ●●●

Perhatikan kembali rumus sin (α - β) = sin α cos β - cos α sin β. Bentuk pada soal memenuhi rumus tersebut dengan α = 75⁰ dan β = 30⁰. Dengan demikian, bentuk tersebut dapat disederhanakan menjadi:

sin 75⁰ cos 30⁰ - cos 75⁰ sin 30⁰ = sin (75⁰ - 30⁰) = sin 45⁰ = 122‾√$\frac{1}{2}\sqrt{2}$.

Jadi, nilai sin 75⁰ cos 30⁰ - cos 75⁰ sin 30⁰ = 122‾√$\frac{1}{2}\sqrt{2}$.

Contoh 3

Jika α dan β merupakan sudut lancip dengan sinα=35$sin\alpha =\frac{3}{5}$ dan cosβ=1213$cos\beta =\frac{12}{13}$ , maka nilai dari sin (α + β) dan sin (α - β) adalah ….

●●● Penyelesaian: ●●●

Diketahui α dan β berada pada kuadran I dengan:

sinα=35$sin\alpha =\frac{3}{5}$

cosβ=1213$cos\beta =\frac{12}{13}$

Untuk memperoleh nilai sin (α + β) dan sin (α - β), kita gunakan rumus sinus jumlah dan selisih dua sudut berikut ini.

sin (α + β) = sin α cos β + cos α sin β

sin (α - β) = sin α cos β - cos α sin β

Oleh karena nilai cos α dan sin β belum diketahui, maka kita tentukan dahulu nilai tersebut dengan memanfaatkan identitas trigonometri sin² α + cos² α = 1.

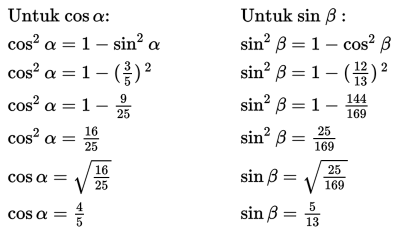
Oleh karena telah diketahui nilai dari sinα=35$sin\alpha =\frac{3}{5}$, cosα=45$cos\alpha =\frac{4}{5}$, sinβ=513$sin\beta =\frac{5}{13}$ , dan cosβ=1213$cos\beta =\frac{12}{13}$, maka dapat kita hitung sinus jumlah dan selisih yang dimaksud, yaitu:

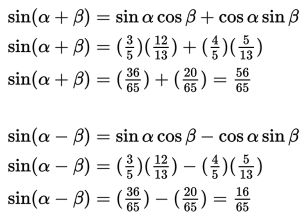
Jadi, nilai dari sin (α + β) dan sin (α - β) berturut-turut adalah 5665$\frac{56}{65}$ dan 1665$\frac{16}{65}$.

Contoh 4

Bentuk sederhana dari sin(π2+x)$sin(\frac{\pi }{2}+x)$ adalah .…

●●● Penyelesaian: ●●●

Untuk menyelesaikan soal tersebut, ingat kembali bahwa:

πrad=180∘→π2rad=90∘$\pi rad={180}^{\circ }\to \frac{\pi }{2}rad={90}^{\circ }$

Dengan menggunakan rumus sinus jumlah dua sudut, diperoleh:

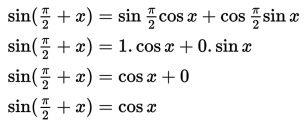
Jadi, bentuk sederhana dari sin(π2+x)$sin(\frac{\pi }{2}+x)$ adalah cos x.

Nah, kamu telah belajar tentang rumus sinus jumlah dan selisih dua sudut. Sekarang, saatnya menguji pemahamanmu dengan mengerjakan soal-soal berikut.