Menghitung Volume Benda Putar dengan Metode Kulit Tabung

Menghitung Volume Benda Putar dengan Metode Kulit Tabung - Seperti yang telah dikemukakan dalam topik sebelumnya, volume benda putar dapat ditentukan dengan menggunakan tiga metode, yaitu

• metode cakram
• metode cincin
• metode kulit/selimut tabung

Nah, dalam topik kali ini kalian akan belajar menentukan volume benda putar dengan menggunakan metode kulit tabung.

Tahukah kalian apa yang dimaksud dengan metode kulit tabung?

Yuk kita perhatikan ilustrasi di bawah ini.

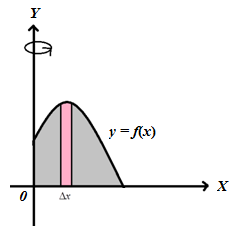
Jika daerah berwarna abu-abu pada ilustrasi di atas kita putar mengelilingi sumbu Y$Y$sejauh 360°$360°$, maka akan kita peroleh benda putar dengan ilustrasi sebagai berikut:

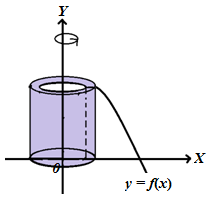
Bangun tersebut merupakan sebuah selubung yang berbentuk tabung (kulit tabung).

Nah, jika benda putar tersebut kita iris tegak lurus dengan sumbu X$X$, maka bidang irisan yang akan kita peroleh adalah sebuah balok, seperti ditunjukkan oleh ilustrasi berikut:

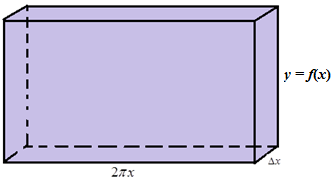
Tahukah kalian berapa volume balok di atas?

Ya, berdasarkan ilustrasi di atas, volume balok adalah ΔV=(2πx)×Δx×f(x)=2πxf(x)Δx$\mathrm{\Delta }V=\left(2\pi x\right)\times \mathrm{\Delta }x\times f\left(x\right)=2\pi xf\left(x\right)\mathrm{\Delta }x$.

Nah, untuk menentukan volume benda putar yang sebenarnya, bidang irisan haruslah semakin tipis. Dengan kata lain, ∆x$∆x$ haruslah semakin kecil.

Berdasarkan konsep jumlah Riemann, jumlah volume dari seluruh balok yang terbentuk adalah 2π∑xxf(x)Δx$2\pi \sum _{x}xf(x)\mathrm{\Delta }x$.

Nah, jika ∆x→0$∆x\to 0$, maka volume benda putar adalah V=2π∫xf(x)dx$V=2\pi \int xf\left(x\right)dx$.

Jadi, apa yang dapat kalian simpulkan?

Benar sekali. Jika suatu daerah yang dibatasi oleh kurva y=f(x)$y=f(x)$ dan terletak pada interval a≤x≤b$a\le x\le b$ diputar mengelilingi sumbu Y$Y$, maka volume benda putar yang terjadi adalah V=2π∫abxf(x)dx$V=2\pi \underset{a}{\overset{b}{\int }}xf(x)dx$.

Dengan demikian, jika suatu daerah yang dibatasi oleh kurva x=g(y)$x=g(y)$ dan terletak pada interval c≤y≤d$c\le y\le d$ diputar mengelilingi sumbu X$X$, maka volume benda putar yang terjadi adalah V=2π∫cdyg(y)dy$V=2\pi \underset{c}{\overset{d}{\int }}yg(y)dy$.

Agar kalian semakin paham dengan metode cincin, yuk kita cermati beberapa contoh soal berikut ini.

Contoh 1

Tentukan volume benda putar yang terjadi jika daerah yang dibatasi oleh kurva y=x2$y=x^2$, sumbu X$X$, dan garis x=1$x=1$, dan garis x=3$x=3$ diputar mengelilingi sumbu Y$Y$ sejauh 360° dengan menggunakan metode kulit tabung.

Penyelesaian:

Sketsa dari daerah yang dimaksud dalam soal adalah sebagai berikut:

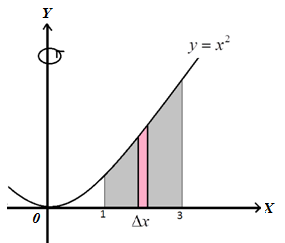
Oleh karena daerah yang terbentuk diputar mengelilingi sumbu Y$Y$, maka yang menjadi batas integrasi adalah x$x$, dari 1$1$ sampai 3$3$.

Dengan demikian,

ΔV=2πx(x2)Δx=2πx3Δx$\mathrm{\Delta }V=2\pi x\left(x^2\right)\mathrm{\Delta }x=2\pi x^3\mathrm{\Delta }x$

V=====2π∫13x3dx2π[14x4]3112π(81−1)802π40π$\begin{array}{lll}V& =& 2\pi \underset{1}{\overset{3}{\int }}{x}^{3}dx\\ & =& 2\pi {\left[\frac{1}{4}{x}^4\right]}_1^3\\ & =& \frac{1}{2}\pi \left(81-1\right)\\ & =& \frac{80}{2}\pi \\ & =& 40\pi \end{array}$

Jadi, volume benda putar yang terjadi adalah 40π$40\pi$ satuan volume.

Contoh 2

Tentukan volume benda putar yang terjadi jika daerah yang dibatasi oleh garis y=x$y=x$, garis x=3$x=3$, dan sumbu X$X$ diputar terhadap sumbu X$X$ sejauh 360° dengan menggunakan metode kulit tabung.

Penyelesaian:

Sketsa dari daerah yang dimaksud dalam soal adalah sebagai berikut:

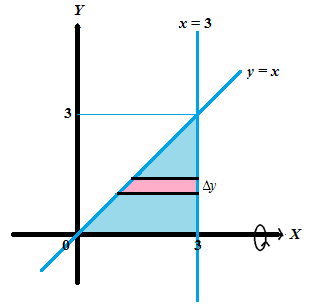
Oleh karena daerah yang terbentuk diputar mengelilingi sumbu X$X$, maka yang menjadi batas integrasi adalah y$y$, dari 0$0$ sampai 3$3$.

Dengan demikian,

ΔV=2πy(3−y)Δy=2π(3y−y2)Δy$\mathrm{\Delta }V=2\pi y\left(3-y\right)\mathrm{\Delta }y=2\pi \left(3y-y^2\right)\mathrm{\Delta }y$

V====2π∫03(3y−y2)dy2π[32y2−13y3]302π[32(9)−13(27)]9π$\begin{array}{lll}V& =& 2\pi \underset{0}{\overset{3}{\int }}\left(3y-y^2\right)dy\\ & =& 2\pi {\left[\frac{3}{2}{y}^2-\frac{1}{3}{y}^3\right]}_{}^{}\end{array}$

$\begin{array}{l}{0}_3^{}\\ & =& 2\pi \left[\frac{3}{2}\left(9\right)-\frac{1}{3}\left(27\right)\right]\\ & =& 9\pi \end{array}$

Jadi, volume benda putar yang terjadi adalah 9π$9\pi$ satuan volume.

Yuk kerjakan latihan soal dalam topik ini untuk menguji tingkat pemahaman kalian.