Ada berapa kemungkinan kedudukan antara dua bidang tersebut?
Benar, ada tiga kemungkinan kedudukan yang mungkin, yaitu dua bidang saling berimpit, sejajar, atau berpotongan.
Kedudukan antara Dua Bidang
Misalkan terdapat dua buah bidang, yaitu bidang dan .
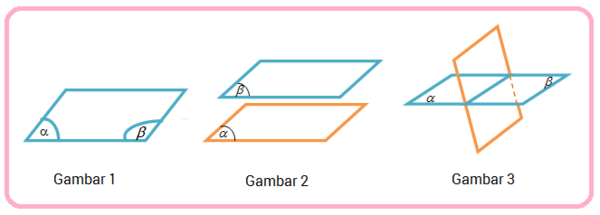
✿ Dua Bidang Berimpit → gambar 1
- Bidang dan dikatakan berimpit jika setiap titik yang terletak pada bidang juga terletak pada bidang , demikian juga sebaliknya.
✿ Dua Bidang Sejajar → gambar 2
- Bidang dan dikatakan sejajar jika kedua bidang tersebut tidak mempunyai titik persekutuan.
✿ Dua Bidang Berpotongan → gambar 3
- Bidang dan dikatakan berpotongan jika kedua bidang tersebut tepat mempunyai sebuah garis persekutuan.
Penjelasan di atas mudah dipahami bukan?
Sebenarnya tiga buah bidang juga dapat saling berpotongan. Yuk kita cari tahu bagaimana kedudukan antara tiga bidang yang saling berpotongan.
Kedudukan antara Tiga Bidang yang Saling Berpotongan
Misalkan ada tiga buah bidang, yaitu bidang , , dan , serta ada tiga garis persekutuan.
Seperti yang telah kalian ketahui, ada tiga kemungkinan kedudukan garis persekutuan, yaitu berimpit (gambar 4), sejajar (gambar 5), atau berpotongan (gambar 6).
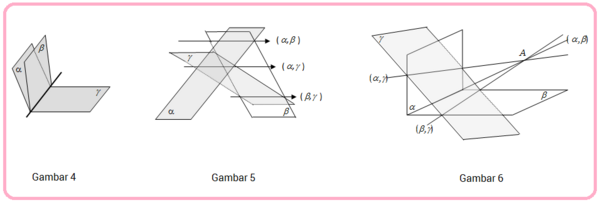
Nah sekarang kalian sudah paham mengenai kedudukan antara tiga bidang yang saling berpotongan bukan?
Yuk kita cermati delapan dalil yang berkaitan dengan dua bidang yang saling sejajar.
Dalil Dua Bidang Sejajar
✿ Dalil I
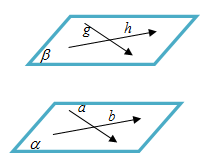
- Jika garis sejajar garis dan garis sejajar garis , garis dan berpotongan dan terletak pada bidang , serta garis dan berpotongan dan terletak pada bidang , maka bidang sejajar dengan bidang .
✿ Dalil II
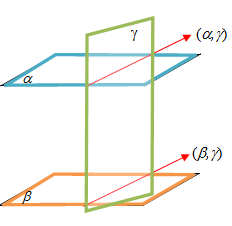
- Jika bidang sejajar dengan bidang dan kedua bidang dipotong oleh bidang , maka garis potong sejajar dengan garis potong .
✿ Dalil III
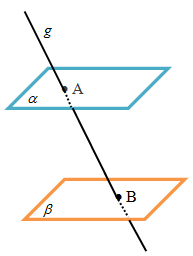
- Jika garis menembus bidang dan bidang sejajar bidang , maka garis juga menembus bidang .
✿ Dalil IV
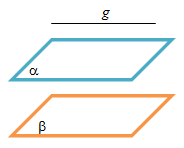
- Jika garis sejajar dengan bidang dan bidang sejajar dengan bidang , maka garis juga sejajar dengan bidang.
✿ Dalil V
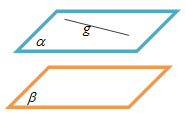
- Jika garis terletak pada bidang dan bidang sejajar dengan bidang , maka garis juga sejajar dengan bidang
✿ Dalil VI
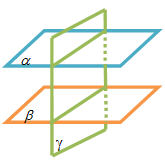
- Jika bidang sejajar dengan bidang dan bidang memotong bidang , maka bidang juga memotong bidang .
✿ Dalil VII
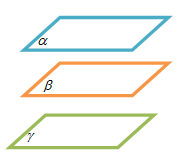
- Jika bidang sejajar dengan bidang dan bidang sejajar dengan bidang , maka bidang sejajar dengan bidang .
✿ Dalil VIII
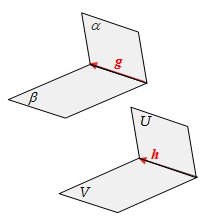
- Jika bidang sejajar dengan bidang , bidang sejajar dengan bidang , bidang dan berpotongan pada garis , serta bidang dan berpotongan pada garis, maka garis sejajar dengan garis .
Agar kalian semakin paham dengan materi di atas, yuk kita cermati tiga contoh soal berikut ini.
Contoh 1
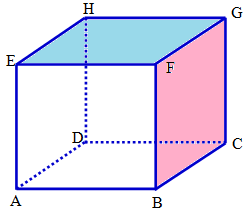
Pada kubus , bidang dan saling sejajar. Adapun bidang yang sejajar dengan bidang adalah bidang .
Contoh 2
Pada kubus , tentukan garis persekutuan antara:
- bidang dan bidang
- bidang dan bidang
- bidang dan bidang
Penyelesaian:
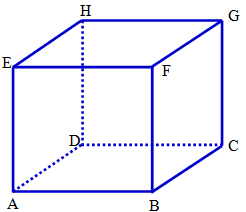
Garis persekutuan antara dua bidang adalah garis potong antara dua bidang tersebut.
Dengan demikian,
- Garis persekutuan antara bidang dan bidang adalah garis .
- Garis persekutuan antara bidang dan bidang adalah garis .
- Garis persekutuan antara bidang dan bidang adalah garis .
Contoh 3
Lukislah garis potong antara bidang dan pada kubus .
Penyelesaian:
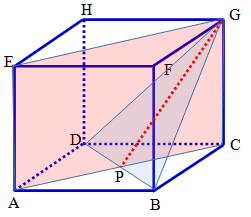
Ada empat langkah yang perlu kalian ikuti untuk melukis garis potong antara bidang dan pada kubus , yaitu:
- Lukis bidang diagonal .
- Lukis bidang .
- Misalkan titik sebagai titik potong atara garis dan .
- Hubungkan titik dan .
Nah, garis adalah garis potong antara bidang dan pada kubus .
Yuk uji pemahaman kalian dengan mengerjakan latihan soal yang ada dalam topik ini.