Kedudukan Garis dalam Bangun Ruang

Kedudukan Garis dalam Bangun Ruang - Pada topik kali ini kalian akan belajar tentang kedudukan garis dalam bangun ruang sisi datar, meliputi kubus, balok, prisma, dan limas.

Hubungan antara Dua Garis

Misalkan kalian mempunyai dua garis, yaitu garis g$g$ dan h$h$.

Tahukah kalian berapa banyak kedudukan yang mungkin antara kedua garis tersebut?

Benar sekali. Ada empat kedudukan yang mungkin, yaitu kedua garis berimpit, sejajar, berpotongan, atau bersilangan.

• Garis g$g$ dikatakan berimpit dengan garis h$h$ jika setiap titik pada garis g$g$ terletak pada garis h$h$.

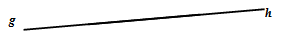
• Garis g$g$ dikatakan sejajar dengan garis h$h$ jika kedua garis tersebut tidak mempunyai titik persekutuan dan sebidang.

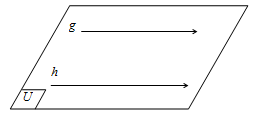
• Garis g$g$ dan h$h$ akan berpotongan jika kedua garis tersebut mempunyai tepat satu titik persekutuan dan sebidang.

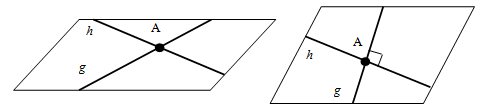
• Garis g$g$ dikatakan bersilangan dengan garis h$h$ jika kedua garis tersebut tidak mempunyai titik persekutuan dan tidak terletak dalam satu bidang.

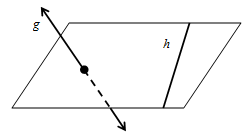
Yuk kita perhatikan tiga contoh berikut.

✿ Contoh 1:

Diberikan kubus ABCD.EFGH$ABCD.EFGH$. Tentukan garis yang sejajar dengan garis BC$BC$.

Penyelesaian:

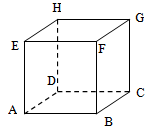
Berdasarkan sketsa di atas,

• Garis BC$BC$ dan AD$AD$ terletak dalam bidang ABCD$ABCD$ dan tidak memiliki titik persekutuan.
• Garis BC$BC$ dan EH$EH$ terletak dalam bidang BCHE$BCHE$ dan tidak memiliki titik persekutuan.
• Garis BC$BC$ dan FG$FG$ terletak dalam bidang BCGF$BCGF$ dan tidak memiliki titik persekutuan.

Dengan demikian, garis BC$BC$ sejajar dengan garis AD$AD$, EH$EH$, dan FG$FG$.

✿ Contoh 2:

Diberikan kubus ABCD.EFGH$ABCD.EFGH$. Tentukan garis yang berpotongan dengan garis EG$EG$.

Penyelesaian:

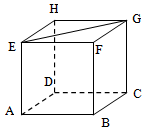
Berdasarkan sketsa di atas, garis yang berpotongan dengan garis EG$EG$ adalah garis AE$AE$, BE$BE$, CE$CE$, DE$DE$, FE$FE$, HE$HE$, AG$AG$, BG$BG$, CG$CG$, DG$DG$, FG$FG$, HG$HG$, dan FH$FH$.

✿ Contoh 3:

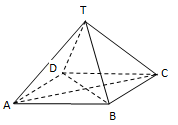
Pada limas T.ABCD$T.ABCD$ di atas, tentukan garis yang bersilangan dengan garis TA$TA$.

Penyelesaian:

Oleh karena

• Garis TA$TA$ tidak mempunyai titik persekutuan dengan garis BC$BC$, BD$BD$, dan CD$CD$.
• Garis TA$TA$ tidak terletak dalam satu bidang dengan garis BC$BC$, BD$BD$, dan CD$CD$.

maka garis TA$TA$ bersilangan dengan garis BC$BC$, BD$BD$, dan CD$CD$.

Hubungan Garis dan Bidang

Ada tiga kemungkinan kedudukan garis terhadap bidang, yaitu garis terletak pada bidang, garis sejajar bidang, dan garis menembus/memotong bidang.

• Sebuah garis dikatakan terletak pada bidang jika garis dan bidang tersebut mempunyai dua titik persekutuan.

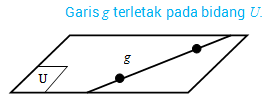
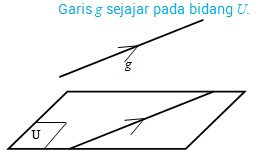
• Sebuah garis dikatakan sejajar dengan bidang jika tidak ada titik persekutuan atau garis tersebut sejajar dengan salah satu garis yang terletak pada bidang tersebut.

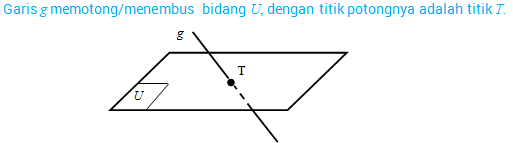
• Sebuah garis dikatakan memotong/menembus bidang jika mempunyai satu titik persekutuan.

Apakah kalian sudah paham mengenai hubungan antara garis dan bidang?

Yuk kita perhatikan tiga contoh berikut.

✿ Contoh 1:

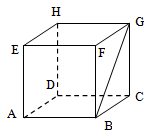
Pada kubus ABCD.EFGH$ABCD.EFGH$ di atas, tentukan bidang yang memuat garis BG$BG$.

Penyelesaian:

Bidang-bidang yang memuat garis BG$BG$ adalah bidang BCGF$BCGF$, ABGH$ABGH$, dan BEG$BEG$.

✿ Contoh 2:

Pada kubus ABCD.EFGH$ABCD.EFGH$ berikut, tentukan bidang yang sejajar dengan garis EH$EH$.

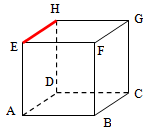
Penyelesaian:

Bidang-bidang yang sejajar dengan garis EH$EH$ adalah bidang ABCD$ABCD$, BCGF$BCGF$, dan ADGF$ADGF$.

✿ Contoh 3:

Tentukan bidang yang dipotong/ditembus oleh garis AG$AG$ pada kubus ABCD.EFGH$ABCD.EFGH$.

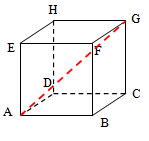
Penyelesaian:

Berdasarkan sketsa di atas,

• Bidang ABCD$ABCD$, ADHE$ADHE$, dan ABFE$ABFE$ berpotongan dengan garis AG$AG$ di titik A$A$.
• Bidang EFGH$EFGH$, BCGF$BCGF$, dan CDHG$CDHG$ berpotongan dengan garis AG$AG$ di titik G$G$.
• Garis AG$AG$ menembus bidang BCHE$BCHE$, BDE$BDE$, dan CFH$CFH$

Nah, kalian sudah selesai mempelajari materi di atas. Yuk kerjakan sepuluh latihan soal dalam topik ini.