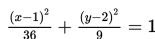Hubungan antara direktriks, titik fokus, dan titik-titik pada Ellips

 | 
Hubungan antara direktriks, titik fokus, dan titik-titik pada Ellips - Setelah kalian mempelajari cara menggambar Ellips, mari kita ingat kembali beberapa unsur ellips, agar kalian dapat menentukan hubungan antara komponen-komponen ellips dengan persamaaan ellips.

Persamaan Ellips dengan pusat (0,0)
Bentuk umum persamaan Ellips adalah :
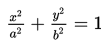
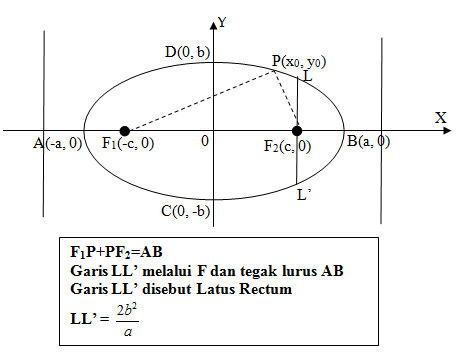
a2 = b2 + c2

Keterangan :
  1. Pusatnya adalah titik O(0,0).
  2. Fokusnya adalah titik F1(-c,0) dan F2(c,0)
  3. Sumbu X adalah sumbu mayor dan dan sumbu Y adalah sumbu minor jika a > b.
  4. Persamaan sumbu mayor adalah y = 0 dan persamaan sumbu minor adalah x = 0.
  5. Ellips akan memotong sumbu X di titik A(-a,0) dan B(a,0) dan memotong sumbu Y di titik C(0, -b) dan D(0,b). Keempat titik itu masing-masing disebut puncak ellips.
  6. AB = 2a disebut sumbu-panjang atau sumbu mayor dan CD = 2b disebut sumbu pendek atau sumbu minor.
  7. Persamaan Direktriks : x = ± a2 + c
  8. Eksentrisitas : e = c/a

Sedangkan
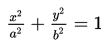
: merupakan persamaan elips dengan pusat O(0,0) yang sumbu panjangnya 2b dan sejajar sumbu Y sedang sumbu pendeknya 2a dan sejajar sumbu X.

II. Persamaan Elips dengan Pusat (α,β)
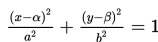
Keterangan: 
1. Pusat (α,β)
2. Puncak A1(α + a, β) dan A2(α - a, β)
3. Fokus F1(α + c, β) dan F2(α - c, β)
4. Sumbu simetri x = α dan y = β 
5. Sumbu panjang = 2a dan sumbu pendek = 2b
6. Persamaan direktriks : x = ± a2 /c + α
7. Eksentrisitas : e = c/a
Sedangkan :
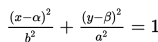
merupakan persamaan elips dengan pusat (α,β) yang sumbu panjangnya 2b dan sejajar sumbu Y sedang sumbu pendeknya 2a dan sejajar sumbu X.
Contoh :
1. Sebuah ellips yang mempunyai pusat (0,0) mempunyai persamaan direktris x = 25/2 dan eksentrisitas : e = 4/5. Tentukan persamaan ellips tersebut!
Jawab :
Dari persamaan direktris : x = 25/2 
-> a2 /c = 25/2
<=> 2a2 = 25c ............(1)
Dari eksentrisitas: ((1+1)/2,(0+4)/2)
-> c/a = 4/5
<=> 4a = 5c .................(2)
Substitusi persamaan (2) ke persamaan (1) diperoleh
2a2 = 25 c 
2a2 = 5.5c 
2a2 = 5.4a
2a2 = 20a 
2a2 – 20a = 0
2a(a – 10) = 0
2a = 0 atau a = 10 
Jadi a = 10 diperoleh 5c = 40 , sehingga c = 8 , 
b2 = a2 – c2 
<=> b2 = 100 - 64 
<=> b = 8
Substitusikan nilai a = 10 dan b = 8 ke persamaan ellips:
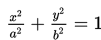
sehingga diperoleh persamaan ellips:
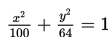
  1. Suatu ellips mempunyai jarak antara kedua fokus =
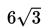
dan eksentrisitas =
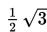
jika pusat ellips tersebut adalah (1, 2). Tentukan persamaan ellips tersebut!
Jawab : 
Fokus =
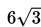
artinya
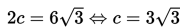
eksentrisitas=
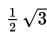
berarti
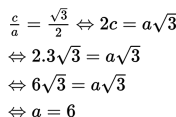
b2 = a2 – c2 = 36 – 27 = 9 sehingga b = 3 
Persamaan ellips dengan a = 6 , b = 3 dan pusat (1, 2) adalah
Share: