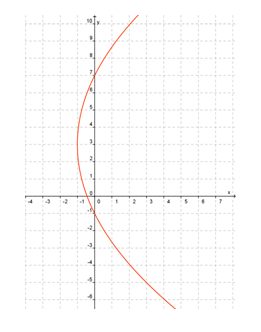
Misalkan kita ingin menggambar parabola x2 = 12y. Benar, bahwa cara yang paling sederhana adalah dengan membuat tabel untuk menentukan pasangan berurut (x,y) sehingga langkah dalam menggambar kurva adalah :
- Tetapkan beberapa pasangan berurut (x,y) yang memenuhi persamaan kurva
- Buat plot titik-titik dalam sistem koordinat Cartesius
- Hubungkan titik-titik sehingga terbentuk suatu kurva mulus.
Selain membuat tabel pasangan berurut, cara apalagi yang dapat kita gunakan apabila ingin mengetahui lebih banyak tentang sketsa grafik parabola?
Kalian dapat mempelajari keterangan selanjutnya karena dalam topik ini kita akan membahas tentang :
- Menggambar sketsa grafik parabola bila persamaannya diberikan.
- Menentukan unsur-unsur parabola jika persamaannya diberikan
- Menentukan persamaan parabola jika beberapa unsurnya diberikan
- Menggambar sketsa grafik parabola jika beberapa unsurnya diberikan
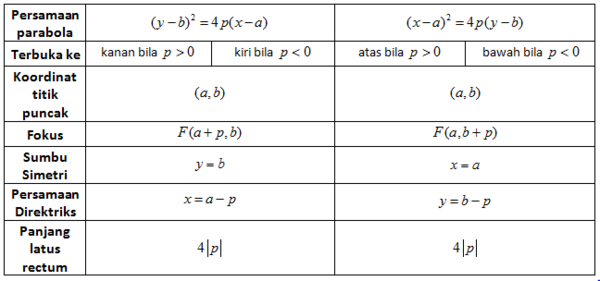
Untuk membantu kalian dalam menyelesaikan masalah tentang parabola, perhatikan keterangan yang dirangkum dalam tabel berikut ini.

Perhatikan pula keterangan dalam tabel berikut :
Marilah kita cermati unsur-unsur parabola x2 = 12y
Parabola x2 = 12y sesuai dengan bentuk umum x2 = 4py dengan nilai p = 3 > 0 sehingga :
- parabola terbuka ke atas.
- mempunyai koordinat titik puncak (0,0)
- koordinat fokus parabola adalah (0,3)
- sumbu simetri adalah sumbu Y
- persamaan garis direktriks adalah y = - 3 -> Apakah kalian melihat hubungannya dengan ordinat titik fokus (0,3)?
- panjang latus rectum yaitu 4p = 4 x 3 =12
Adapun sketsa grafik parabola x2 = 12y adalah sebagai berikut :
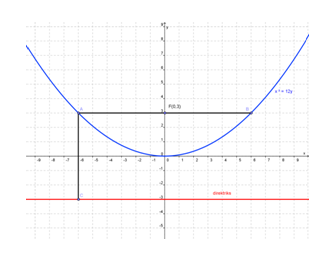
Pada gambar di atas, panjang AF sama dengan panjang AC.
Agar kalian lebih jelas dalam menggambar parabola, maka perhatikan beberapa contoh berikut ini.
Contoh 1 : Grafik parabola x2 = 8y ditunjukkan oleh….
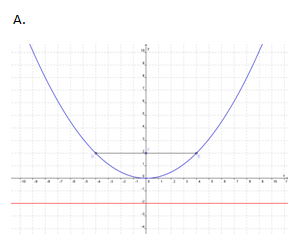
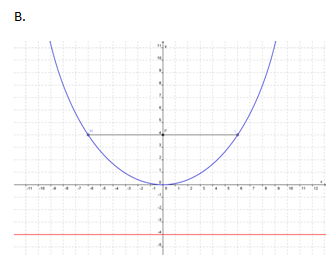
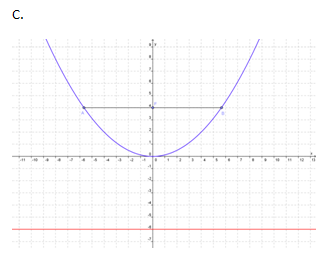
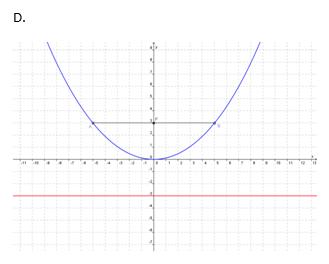
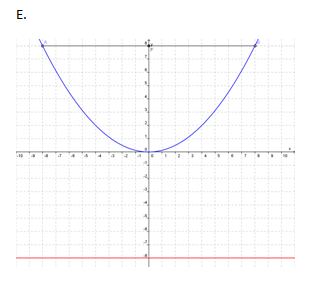
Pembahasan
Dari persamaan parabola x2 = 8y dapat ditentukan bahwa 8y = 4py <=> p = 2 sehingga koordinat titik fokus adalah (0 , 2) dan panjang latus rectum = 8
Jadi, jawaban yang benar adalah A.
Contoh 2 : Perhatikan gambar berikut :
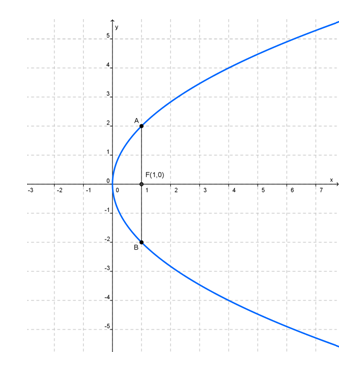
Tentukan persamaan parabola yang sesuai dengan gambar di atas!
Pembahasan :
Parabola memiliki sumbu simetri pada sumbu X sehingga persamaan umumnya adalah :
y2 = 4px
dengan titik fokus (p,0)
y2 = 4px
dengan titik fokus (p,0)
Selanjutnya, karena koordinat titik fokusnya adalah (1,0) maka nilai p adalah 1.
Dengan demikian, persamaan parabola yang dicari adalah y2 = 4x
Contoh 3 : Tentukan persamaan parabola yang mempunyai titik puncak (- 1,3) dan koordinat titik fokus (3,3). Buatlah sketsalah grafik parabola tersebut!
Pembahasan :
Parabola mempunyai titik puncak (- 1,3) dan koordinat titik fokus (3,3) maka persamaan yang sesuai adalah :
(y – b)2 = 4p(x – a)
(y – b)2 = 4p(x – a)
Karena koordinat titik puncak adalah (-1,3) maka a = -1 dan b = 3
Karena jarak antara absis titik puncak dan fokus adalah 4, maka persamaan parabola yang dicari adalah :
(y – 3)2 = 16(x + 1)
(y – 3)2 = 16(x + 1)
Sketsa parabola (y – 3)2 = 16(x + 1) adalah :