Uji hipotesis dilakukan dengan tujuan memperoleh gambaran mengenai suatu populasi dari sampel.
Hipotesis adalah dugaan sementara sehingga harus diuji kebenarannya. Dalam pengujian hipotesis, kita akan sering menggunakan istilah ”menerima” atau ”menolak” suatu hipotesis. Namun demikian perlu kalian sadari bahwa dalam pengujian hipotesis, kita tidak akan menyimpulkan bahwa hipotesis itu benar atau salah melainkan kita akan menyimpulkan bahwa hipotesis dapat diterima atau ditolak berdadasarkan apa yang diperoleh dari sampel.
Secara garis besar, hipotesis dibedakan atas hipotesis nol yang biasanya dilambangkan dengan H0 dan hipotesis tandingan atau hipotesis alternatif dilambangkan dengan Haatau H1.
Langkah-Langkah Pengujian Hipotesis
1. Menentukan hipotesis nol (H0) dan hipotesis alternatifnya (H1)
Misalkan yang diuji adalah parameter ϴ (dalam penggunaannya nanti ϴ dapat berupa rata-rata μ, proporsi π, simpangan baku σ, dan lain-lain).
Jika hipotesis mengandung pengertian sama maka pasangan H0 dan H1 adalah
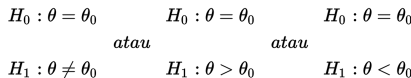
Jika hipotesis mengandung pengertian maksimum maka pasangan H0 dan H1 adalah
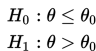
Jika hipotesis mengandung pengertian minimum maka pasangan H0 dan H1 adalah
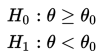
2. Menentukan taraf signifikansi (α)
Dalam memilih tingkat signifikansi kita harus memperhatikan hasil penelitian terdahulu terhadap penelitian sejenis. Masing-masing bidang ilmu mempunyai standar yang berbeda dalam menentukan tingkat signifikansi. Ilmu sosial biasanya menggunakan tingkat signifikansi antara 90% (α 10%) sampai 95% (α 5%), sedangkan ilmu-ilmu eksakta biasanya menggunakan tingkat signifikansi antara 98% (α 2%) sampai 99% (α 1%).
3. Memilih statistik uji yang sesuai
Setelah menentukan tingkat signifikansi langkah selanjutnya adalah menentukan uji statistik yang akan digunakan. Hal ini karena masing-masing uji statistik memerlukan asumsi yang berbeda dalam penerapannya. Perlu kalian ingat lagi mengenai penggunaan nilai z dan t.
Jika σ (simpangan baku populasi) diketahui, maka gunakan rumus berikut ini :
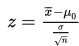
Jika σ tidak diketahui, maka gunakan rumus berikut ini :
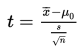
Selanjutnya, pada pengujian kesamaan dua rata-rata pada data yang berpasangan (dependen), ada dua rumus yang dapat digunakan.
Jika σ1 = σ2 = σ dan σ diketahui, maka gunakan rumus :

Jika σ1 = σ2 = σ dan σ tidak diketahui, maka gunakan rumus :

4. Menentukan Kriteria Keputusan
Kriteria keputusan berkaitan erat dengan daerah kritis. Adapun penentuan daerah kritis berkaitan dengan H1.
- Jika H1 mempunyai rumusan tidak sama dengan maka distribusi statistik yang digunakan adalah normal untuk angka z dan didapat dua daerah kritis pada ujung–ujung distribusi. Adapun luas daerah kritis atau daerah penolakan pada tiap ujung adalah α/2. Pengujian hipotesis ini dinamakan uji dua pihak karena terdapat dua daerah penolakan.
- Jika H1 mempunyai rumusan lebih dari, maka daerah kritis berada di ujung sebelah kanan dan luasnya adalah α.
- Jika H1 mempunyai rumusan kurang dari, maka daerah kritis berada di ujung sebelah kiri dan luasnya adalah α.
5. Menarik Kesimpulan
Tahap terakhir adalah pengambilan keputusan untuk menolak atau tidak menolak H0. Sebagai contoh, mari kita perhatikan gambar di bawah ini.
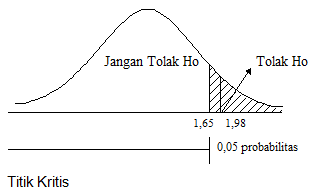
Jika hasil perhitungan yang kalian dapatkan sebesar 1,98 maka H0 ditolak pada level kepercayaan 95%. H0 ditolak karena z hasil perhitungan berada pada daerah penolakan H0 , yaitu disebelah kanan nilai z = 1,65.
Mari kita perhatikan contoh berikut ini.
Suatu perusahaan shampo memproduksi shampo dalam bentul botol dengan rata-rata isi 100 ml. Sepuluh sampel shampo dipilih secara acak dengan isi 97 ml, 98 ml, 102 ml, 103 ml, 99 ml, 103 ml, 101 ml, 104 ml, 98 ml, 101 ml. Ujilah hipotesis bahwa isi botol tersebut rata-rata 100 ml dengan taraf signifikansi 0,01 dan diasumsikan bahwa isi tersebut menyebar normal.
Penyelesaian :
Hipotesis
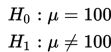
Taraf signifikansi : α = 0,01
Statistik Uji
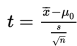
Kriteria Keputusan
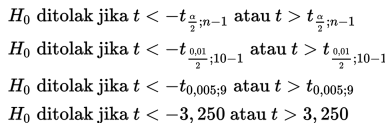
Perhitungan

Kesimpulan
Karena t = 0,814 < 3,250 maka H0 diterima.
Jadi, dapat disimpulkan bahwa isi rata-rata botol shampo tersebut adalah 100 ml.