Pada topik sebelumnya, kalian telah mempelajari bahwa distribusi binomial adalah suatu distribusi peluang yang dapat digunakan bilamana suatu proses sampling dapat diasumsikan sesuai dengan proses Bernoulli. Misalnya, dalam perlemparan sekeping uang logam sebanyak 5 kali, hasil setiap ulangan mungkin muncul sisi gambar atau sisi angka.
Begitu pula, bila satu buah jeruk diambil dari sebuah keranjang maka kemungkinan yang terambil adalah jeruk yang manis atau asam. Ulangan-ulangan tersebut bersifat bebas dan peluang keberhasilan setiap ulangan tetap sama, yaitu sebesar ½.
Mari kita ingat kembali mengenai rumus distribusi peluang untuk variabel acak binomial.
Jika percobaan binomial mempunyai peluang keberhasilan p dan kegagalan q = 1 – p , maka distribusi peluang untuk variabel acak binomial X yaitu banyaknya keberhasilan dalam n percobaan yang bebas adalah
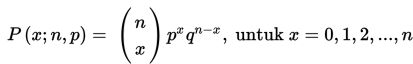
Agar mudah membedakan p dengan q, kalian harus dapat menetapkan mana kejadian yang sukses dan mana kejadian yang gagal. Hal yang paling mudah dilakukan adalah menetapkan kejadian yang menjadi pertanyaan atau ditanyakan sebagai kejadian sukses.
Contoh 1 :
Suatu suku cadang dapat menahan uji guncangan tertentu dengan peluang 0,75. Tentukan peluang bahwa tepat 2 dari 4 suku cadang yang diuji tidak akan rusak jika kejadian uji gancangan saling bebas!
Penyelesaian :
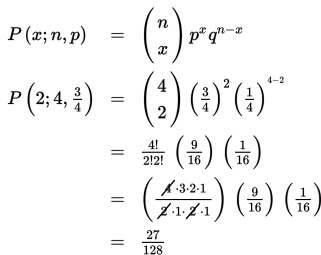
Jadi, peluang bahwa tepat 2 dari 4 suku cadang yang diuji tidak akan rusak adalah27/128.
Contoh 2 :
Kepala bagian produksi PT GARUDA CELL melaporkan bahwa rata-rata produksi ponsel yang rusak adalah sebesar 15%. Jika dari total produksi tersebut diambil secara acak sebanyak 4 buah ponsel, berapakah peluang bahwa 2 ponsel yang diambil ternyata rusak?
Penyelesaian :
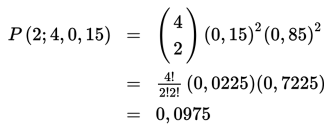
Hasil perhitungan ini menunjukkan bahwa dengan 0,0975 atau 9,75% dari sampel acak sebanyak 4 buah ponsel dan rata-rata produk rusak setiap kali produksi adalah sebesar 15%, dapat dikatakan kecil. Namun pada kenyataannya, meskipun dilihat secara presentase kecil (9,75%) tetapi produk rusak harus tetap dikurangi atau bahkan dihilangkan untuk mengurangi kerugian.
Apa sekarang kalian sudah paham mengenai penggunaan distribusi binomial?