Dilatasi yang berpusat di P (a, b) dengan Faktor Skalar k

Dilatasi yang berpusat di P (a, b) dengan Faktor Skalar k - Coba kalian sebutkan aplikasi dilatasi dalam masalah nyata.

Ya, ada banyak masalah nyata yang berhubungan dengan dilatasi. Sebagai contoh penggunaan mikroskop untuk memperbesar foto penampang. Konsep dilatasi juga digunakan dalam pembuatan peta. Dalam hal ini, faktor skala memegang peranan penting.

Pada topik sebelumnya, kalian telah belajar tentang dilatasi yang berpusat di titik O(0,0)$O(0,0)$ dengan faktor skala k$k$. Nah, dalam topik ini kalian juga akan belajar tentang dilatasi, namun pusat dilatasinya adalah P(a,b)$P(a,b)$.

Konsep Dasar

Seperti yang telah kalian ketahui, pusat dilatasi dan faktor skala memegang peranan penting dalam dilatasi.

Berikut ini adalah perbedaan hasil dilatasi dengan memperhatikan nilai dari faktor skala k$k$:

• Jika k>1$k>1$, maka bayangan benda diperbesar dan kedudukan benda dan bayangan adalah sepihak terhadap pusat dilatasi.
• Jika 0<k<1$0<k<1$, maka bayangan benda diperkecil dan kedudukan benda dan bayangan adalah sepihak terhadap pusat dilatasi.
• Jika −1<k<0$-1<k<0$, maka bayangan benda diperkecil dan kedudukan benda dan bayangan berlawanan pihak terhadap pusat dilatasi.
• Jika k<−1$k<-1$ maka bayangan benda diperbesar dan kedudukan benda dan bayangan berlawanan pihak terhadap pusat dilatasi.

Nah, tahukah kalian perbedaan antara hasil dilatasi dengan pusat O(0,0)$O(0,0)$ dan P(a,b)$P(a,b)$?

Mari kita temukan jawabannya dengan memperhatikan ilustrasi berikut ini.

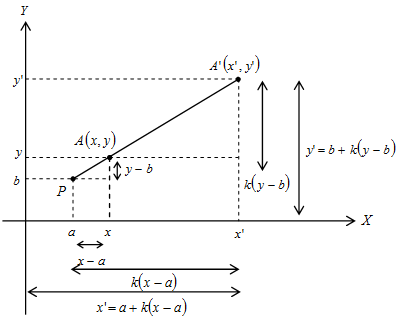
Pada ilustrasi di atas, tampak bahwa absis dan ordinat dari titik A$A$ dan A′$A^{\prime }$ mengalami pergeseran.

Pergeseran pada absis dari titik A$A$ dan A′$A^{\prime }$ berturut-turut adalah

• x⎯⎯⎯=x−a$\overline{x}=x-a$
• x′⎯⎯⎯⎯⎯=x′−a$\overline{x^{\prime }}=x^{\prime }-a$

Adapun pergeseran pada ordinat dari titik A$A$ dan A′$A^{\prime }$ berturut-turut adalah

• y⎯⎯⎯=y−b$\overline{y}=y-b$
• y′⎯⎯⎯⎯⎯=y′−b$\overline{y^{\prime }}=y^{\prime }-b$

Dengan demikian,

• x′⎯⎯⎯⎯⎯=kx⎯⎯⎯⇔x′−a=k(x−a)⇔x′=a+k(x−a)$\overline{x^{\prime }}=k\overline{x}\iff x^{\prime }-a=k(x-a)\iff x^{\prime }=a+k(x-a)$
• y′⎯⎯⎯⎯⎯=ky⎯⎯⎯⇔y′−b=k(y−b)⇔y′=b+k(y−b)$\overline{y^{\prime }}=k\overline{y}\iff y^{\prime }-b=k(y-b)\iff y^{\prime }=b+k(y-b)$

Jadi, koordinat bayangan dari titik A(x,y)$A(x,y)$ oleh dilatasi [P(a,b),k]$[P(a,b),k]$ adalah A′(a+k(x−a),b+k(y−b))$A^{\prime }(a+k(x-a),b+k(y-b))$.

Notasi: A(x,y)−→−−−−[(a,b),k]A′(a+k(x−a),b+k(y−b)) $A(x,y)\stackrel{[(a,b),k]}{\to }{A}^{\prime }(a+k(x-a),b+k(y-b))$.

Persamaan matriks yang sesuai dengan dilatasi ini adalah sebagai berikut: (x′y′ )=(k00k )(x−ay−b )+(ab )$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{cc}k& 0\\ 0& k\end{array}\right)\left(\begin{array}{c}x-a\\ y-b\end{array}\right)+\left(\begin{array}{c}a\\ b\end{array}\right)$

Agar kalian semakin jelas, mari kita cermati beberapa contoh berikut.

Contoh 1

Tentukan bayangan titik P(2,−1)$P(2,-1)$ oleh dilatasi terhadap titik pusat A(3,4)$A(3,4)$ dengan faktor skala (-3).

Penyelesaian:

Jika P′(x′,y′)$P^{\prime }(x^{\prime },y^{\prime })$ adalah koordinat titik bayangan yang dimaksud, maka

(x′y′ )=====(k00k )(x−ay−b )+(ab )(−300−3 )(2−3−1−4 )+(34 )(−300−3 )(−1−5 )+(34 )(315 )+(34 )(619 )  $\begin{array}{lll}\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)& =& \left(\begin{array}{cc}k& 0\\ 0& k\end{array}\right)\left(\begin{array}{c}x-a\\ y-b\end{array}\right)+\left(\begin{array}{c}a\\ b\end{array}\right)\\ & =& \left(\begin{array}{cc}-3& 0\\ 0& -3\end{array}\right)\left(\begin{array}{c}2-3\\ -1-4\end{array}\right)+\left(\begin{array}{c}3\\ 4\end{array}\right)\\ & =& \left(\begin{array}{cc}-3& 0\\ 0& -3\end{array}\right)\left(\begin{array}{c}-1\\ -5\end{array}\right)+\left(\begin{array}{c}3\\ 4\end{array}\right)\\ & =& \left(\begin{array}{c}3\\ 15\end{array}\right)+\left(\begin{array}{c}3\\ 4\end{array}\right)\\ & =& \left(\begin{array}{c}6\\ 19\end{array}\right)\end{array}$

Jadi, bayangan titik P(2,−1)$P(2,-1)$ oleh dilatasi terhadap titik pusat A(3,4)$A(3,4)$ dengan faktor skala (-3) adalah P(6,19)$P(6,19)$.

Contoh 2

Tentukan persamaan bayangan garis y=3x+2 $y=3x+2$ oleh dilatasi dengan pusat P(21)$P(21)$dan faktor skala 4.

Penyelesaian:

Jika A′(x′,y′)$A^{\prime }(x^{\prime },y^{\prime })$ adalah koordinat titik bayangan yang dimaksud, maka

(x′y′ )====(k00k )(x−ay−b )+(ab )(4004 )(x−2y−1 )+(21 )(4x−84y−4 )+(21 )(4x−64y−3 )  $\begin{array}{lll}\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)& =& \left(\begin{array}{cc}k& 0\\ 0& k\end{array}\right)\left(\begin{array}{c}x-a\\ y-b\end{array}\right)+\left(\begin{array}{c}a\\ b\end{array}\right)\\ & =& \left(\begin{array}{cc}4& 0\\ 0& 4\end{array}\right)\left(\begin{array}{c}x-2\\ y-1\end{array}\right)+\left(\begin{array}{c}2\\ 1\end{array}\right)\\ & =& \left(\begin{array}{c}4x-8\\ 4y-4\end{array}\right)+\left(\begin{array}{c}2\\ 1\end{array}\right)\\ & =& \left(\begin{array}{c}4x-6\\ 4y-3\end{array}\right)\end{array}$

Berdasarkan uraian di atas, kita peroleh hasil sebagai berikut:

1. x′=4x−6⇔x=x′+64 $x^{\prime }=4x-6\iff x=\frac{x^{\prime }+6}{4}$
2. y′=4y−3⇔y=y′+34 $y^{\prime }=4y-3\iff y=\frac{y^{\prime }+3}{4}$

Dengan demikian,

y=3x+2⇔y′+34=3(x′+64)+2⇔y′+34=3x′+184+2⇔y′+34=3x′+18+84⇔y′+3=3x′+26⇔y′=3x′+23  $\begin{array}{rl}& y=3x+2\\ & \iff \frac{y^{\prime }+3}{4}=3\left(\frac{x^{\prime }+6}{4}\right)+2\\ & \iff \frac{y^{\prime }+3}{4}=\frac{3x^{\prime }+18}{4}+2\\ & \iff \frac{y^{\prime }+3}{4}=\frac{3x^{\prime }+18+8}{4}\\ & \iff y^{\prime }+3=3x^{\prime }+26\\ & \iff y^{\prime }=3x^{\prime }+23\end{array}$

Bayangan garis y=3x+2$y=3x+2$ oleh dilatasi terhadap titik pusat P(2,1)$P(2,1)$ dan faktor skala 4 adalah garis y=3x+23$y=3x+23$.