Transformasi Regangan Searah Sumbu Y

Transformasi Regangan Searah Sumbu Y - Pada topik sebelumnya kalian telah belajar mengenai transformasi regangan searah sumbu

X$X$ dengan faktor skala k$k$. Nah, dalam topik ini kalian juga akan belajar mengenai transformasi regangan, namun arah regangan yang akan kalian pelajari adalah regangan searah sumbu Y$Y$.

Apa perbedaan antara transformasi regangan searah sumbu X$X$ dan Y$Y$?

Yuk kita temukan jawabannya dalam topik ini.

Konsep Dasar

Sebelum kita membahas masalah transformasi regangan searah sumbu Y$Y$, mari kita cermati ilustrasi berikut.

Diketahui persegipanjang OABC$OABC$ dengan O(0,0)$O(0,0)$, A(4,0)$A(4,0)$, B(4,3)$B(4,3)$, dan C(0,3)$C(0,3)$ditransformasikan terhadap matriks (1002 )$\left(\begin{array}{cc}1& 0\\ 0& 2\end{array}\right)$. Nah, tugas kalian adalah menentukan bayangan dari persegipanjang OABC$OABC$.

Berdasarkan konsep transformasi, bayangan keempat titik sudut persegipanjang OABC$OABC$ dapat ditentukan seperti berikut:

(x′Ay′Ax′By′Bx′Cy′Cx′Dy′D )===(1002 )(xAyAxByBxCyCxDyD )(1002 )(00404303 )(00404606 ) $\begin{array}{lll}\left(\begin{array}{cccc}{x}_A^{\prime }& x_B^{\prime }& x_C^{\prime }& x_D^{\prime }\\ y_A^{\prime }& y_B^{\prime }& y_C^{\prime }& y_D^{\prime }\end{array}\right)& =& \left(\begin{array}{cc}1& 0\\ 0& 2\end{array}\right)\left(\begin{array}{cccc}{x}_A& x_B& x_C& x_D\\ y_A& y_B& y_C& y_D\end{array}\right)\\ & =& \left(\begin{array}{cc}1& 0\\ 0& 2\end{array}\right)\left(\begin{array}{cccc}0& 4& 4& 0\\ 0& 0& 3& 3\end{array}\right)\\ & =& \left(\begin{array}{cccc}0& 4& 4& 0\\ 0& 0& 6& 6\end{array}\right)\end{array}$

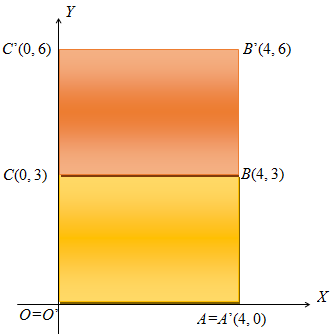
Berdasarkan uraian di atas, dapat disimpulkan bahwa bayangan persegipanjang OABC$OABC$adalah persegi O′A′B′C′$O^{\prime }{A}^{\prime }{B}^{\prime }{C}^{\prime }$ dengan O′(0,0)$O^{\prime }(0,0)$, A′(4,0)$A^{\prime }(4,0)$, B′(4,6)$B^{\prime }(4,6)$, dan C′(0,6)$C^{\prime }(0,6)$.

Apa yang dapat kalian simpulkan dari ilustrasi di atas?

Ya, transformasi (1002 )$\left(\begin{array}{cc}1& 0\\ 0& 2\end{array}\right)$ menyebabkan titik-titik pada persegipanjang OABC$OABC$ yang terletak pada sumbu X$X$ dipetakan pada dirinya sendiri, sedangkan titik-titik yang tidak terletak pada sumbu X$X$ dipetakan dalam arah sejajar sumbu Y$Y$ sedemikian hingga ordinatnya menjadi dua kali ordinat semula, dengan absis tetap.

Nah, transformasi di atas disebut dengan transformasi regangan (stretch) searah sumbu Y$Y$ dengan faktor skala k=2$k=2$.

Secara umum, transformasi regangan searah sumbu Y$Y$ dengan faktor skala k$k$ akan memetakan titik A(x,y)$A(x,y)$ ke titik A′(x′,y′)=A′(x,ky)$A^{\prime }(x^{\prime },y^{\prime })=A^{\prime }(x,ky)$.

Nah, persamaan matriks untuk transformasi regangan searah sumbu Y$Y$ dengan faktor skala k$k$ adalah (x′y′ )=(100k )(xy )$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{cc}1& 0\\ 0& k\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)$.

Agar kalian lebih paham dengan materi di atas, mari kita cermati beberapa contoh berikut.

Contoh 1

Tentukan bayangan titik A(−7,5)$A(-7,5)$ dan B(3,−5)$B(3,-5)$ oleh transformasi regangan searah sumbu Y$Y$ dengan faktor skala k=5$k=5$.

Penyelesaian:

Oleh karena matriks transformasi dari regangan searah sumbu Y$Y$ dengan faktor skala k$k$adalah (100k )$\left(\begin{array}{cc}1& 0\\ 0& k\end{array}\right)$, maka bayangan titik A(−7,5)$A(-7,5)$ dan B(3,−5)$B(3,-5)$ dapat ditentukan dengan cara sebagai berikut:

(x′Ay′Ax′By′B )===(100k )(xAyAxByB )(1005 )(−753−5 )(−7253−25 ) $\begin{array}{lll}\left(\begin{array}{cc}{x}_A^{\prime }& x_B^{\prime }\\ y_A^{\prime }& y_B^{\prime }\end{array}\right)& =& \left(\begin{array}{cc}1& 0\\ 0& k\end{array}\right)\left(\begin{array}{cc}{x}_A& x_B\\ y_A& y_B\end{array}\right)\\ & =& \left(\begin{array}{cc}1& 0\\ 0& 5\end{array}\right)\left(\begin{array}{cc}-7& 3\\ 5& -5\end{array}\right)\\ & =& \left(\begin{array}{cc}-7& 3\\ 25& -25\end{array}\right)\end{array}$

Jadi, bayangan titik A(−7,5)$A(-7,5)$ dan B(3,−5)$B(3,-5)$ oleh transformasi regangan searah sumbu Y$Y$ dengan faktor skala k=5$k=5$ adalah A′(−7,25)$A^{\prime }(-7,25)$ dan B′(3,−25)$B^{\prime }(3,-25)$.

Coba kalian perhatikan bayangan titik A$A$ dan B$B$ pada contoh di atas.

Hanya ordinatnya saja yang berubah bukan?

Ordinat titik bayangan menjadi lima kali ordinat titik semula.

Contoh 2

Titik A′(−12,4)$A^{\prime }(-12,4)$ adalah bayangan titik A(−12,16)$A(-12,16)$ oleh transformasi regangan searah sumbu Y$Y$ dengan faktor skala k$k$. Tentukan bayangan titik R(7,−20)$R(7,-20)$ oleh transformasi regangan searah sumbu Y$Y$ dengan faktor skala k$k$.

Penyelesaian:

Oleh karena titik A′(−12,4)$A^{\prime }(-12,4)$ adalah bayangan titik A(−12,16)$A(-12,16)$ oleh transformasi regangan searah sumbu Y$Y$ dengan faktor skala k$k$, maka

(100k )(−1216 )=(−124 )⇔(−1216k )=(−124 )⇔k=14 $\begin{array}{rl}& \left(\begin{array}{cc}1& 0\\ 0& k\end{array}\right)\left(\begin{array}{c}-12\\ 16\end{array}\right)=\left(\begin{array}{c}-12\\ 4\end{array}\right)\\ & \iff \left(\begin{array}{c}-12\\ 16k\end{array}\right)=\left(\begin{array}{c}-12\\ 4\end{array}\right)\\ & \iff k=\frac{1}{4}\end{array}$

Dengan demikian, bayangan titik R(7,−20)$R(7,-20)$ dapat ditentukan dengan cara sebagai berikut:

(x′Ry′R )===(100k )(xRyR )(10014 )(7−20 )(7−5 ) $\begin{array}{lll}\left(\begin{array}{c}{x}_R^{\prime }\\ y_R^{\prime }\end{array}\right)& =& \left(\begin{array}{cc}1& 0\\ 0& k\end{array}\right)\left(\begin{array}{c}{x}_R\\ y_R\end{array}\right)\\ & =& \left(\begin{array}{cc}1& 0\\ 0& \frac{1}{4}\end{array}\right)\left(\begin{array}{c}7\\ -20\end{array}\right)\\ & =& \left(\begin{array}{c}7\\ -5\end{array}\right)\end{array}$

Jadi, bayangan titik R(7,−20)$R(7,-20)$ oleh transformasi regangan di atas adalah R′(7,−5)$R^{\prime }(7,-5)$.

Nah, bagaimanakah bayangan sebuah kurva terhadap transformasi regangan searah sumbu Y$Y$ dengan faktor skala k$k$?

Yuk kita cari tahu jawabannya dalam contoh berikut.

Contoh 3

Tentukan bayangan kurva y=2(x−1)2+3$y=2{(x-1)}^2+3$ oleh transformasi regangan searah sumbu Y$Y$ dengan faktor skala k=2$k=2$.

Penyelesaian:

Oleh karena matriks transformasi dari regangan searah sumbu Y$Y$ dengan faktor skala k$k$adalah (100k )$\left(\begin{array}{cc}1& 0\\ 0& k\end{array}\right)$, maka bayangan titik (x,y)$(x,y)$ dapat ditentukan dengan cara sebagai berikut:

(x′y′ )=(1002 )(xy )$\begin{array}{lll}\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)& =& \left(\begin{array}{cc}1& 0\\ 0& 2\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)\end{array}$

Oleh karena AX=B⇔X=A−1B$AX=B\iff X=A^{-1}B$, maka

(xy )===12−0(2001 )(x′y′ )12(2x′y′ )(x′12y′ ) $\begin{array}{lll}\left(\begin{array}{c}x\\ y\end{array}\right)& =& \frac{1}{2-0}\left(\begin{array}{cc}2& 0\\ 0& 1\end{array}\right)\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)\\ & =& \frac{1}{2}\left(\begin{array}{c}2x^{\prime }\\ y^{\prime }\end{array}\right)\\ & =& \left(\begin{array}{c}{x}^{\prime }\\ \frac{1}{2}{y}^{\prime }\end{array}\right)\end{array}$

Jika kita subtitusikan hasil di atas ke dalam persamaan kurva y=2(x−1)2+3$y=2{(x-1)}^2+3$, maka akan kita peroleh persamaan bayangan sebagai berikut:

y⇔12y′⇔y′===2(x−1)2+32(x′−1)2+34(x′−1)2+6 $\begin{array}{lll}y& =& 2{\left(x-1\right)}^2+3\\ \iff \frac{1}{2}{y}^{\prime }& =& 2{\left(x^{\prime }-1\right)}^2+3\\ \iff y^{\prime }& =& 4{\left(x^{\prime }-1\right)}^2+6\end{array}$

Jadi, bayangan kurva y=2(x−1)2+3$y=2{(x-1)}^2+3$ oleh transformasi regangan searah sumbu Y$Y$dengan faktor skala k=2$k=2$ adalah kurva y=4(x−1)2+6$y=4{(x-1)}^2+6$.

Yuk kerjakan sepuluh latihan soal dalam topik ini.