Sifat-Sifat Khusus Integral Tentu

Sifat-Sifat Khusus Integral Tentu - Pada topik sebelumnya kalian telah belajar tentang sifat-sifat integral tentu. Nah, pada topik kali ini kalian akan belajar tentang sifat-sifat khusus dari integral tentu pada sebuah fungsi genap, fungsi ganjil, dan fungsi periodik.

Apakah kalian masih ingat dengan apa yang dimaksud fungsi genap, fungsi ganjil, dan fungsi periodik?

Yuk kita ingat kembali ketiga fungsi tersebut dengan mencermati gambar berikut ini.

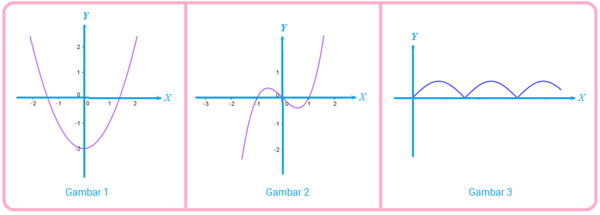
Gambar 1 merupakan grafik fungsi genap dan gambar 2 merupakan grafik fungsi ganjil. Jika kalian perhatikan, grafik fungsi genap simetri terhadap sumbu Y$Y$, sedangkan grafik fungsi ganjil simetri terhadap sumbu X$X$.

Nah, gambar 3 merupakan grafik fungsi periodik, yang menggambarkan perulangan pada interval tertentu.

Tahukah kalian mengapa integral dari sebuah fungsi genap, ganjil, dan periodik dikatakan mempunyai sifat khusus?

Yuk kita temukan jawabannya dalam topik ini.

Fungsi Genap

Fungsi f$f$ merupakan fungsi genap jika dan hanya jika untuk sebarang nilai x$x$ pada domain fungsi berlaku persamaan: f(−x)=f(x)$f(-x)=f(x)$.

Sebagai ilustrasi, misalkan fungsi f$f$ kontinu pada interval [−a,a]$[-a,a]$, dengan grafik fungsi sebagai berikut:

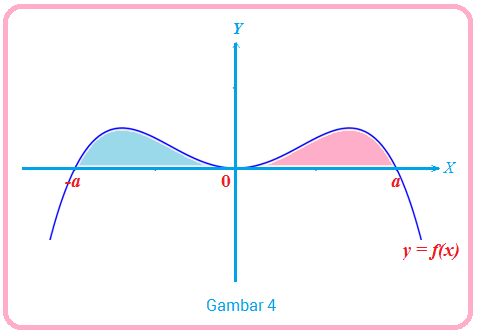
Berdasarkan sifat intergral tentu, luas daerah berwarna pada grafik di atas adalah ∫−aaf(x)dx=∫−a0f(x)dx+∫0af(x)dx$\underset{-a}{\overset{a}{\int }}f(x)dx=\underset{-a}{\overset{0}{\int }}f(x)dx+\underset{0}{\overset{a}{\int }}f(x)dx$.

Nah, jika kita misalkan u=−x$u=-x$, maka

• x=a$x=a$ ⇒ u=−a$u=-a$
• x=0$x=0$ ⇒ u=0$u=0$
• f(x)=f(−u)=f(u)$f(x)=f(-u)=f(u)$ → fungsi genap
• dudx=d(−x)dx⇔dudx=−1⇔dx=−du$\frac{du}{dx}=\frac{d\left(-x\right)}{dx}\iff \frac{du}{dx}=-1\iff dx=-du$

Akibatnya,

∫x=−a0f(x)dx===∫u=a0f(u)(−du)−∫u=a0f(u)du∫u=0af(u)du$\begin{array}{lll}\underset{x=-a}{\overset{0}{\int }}f(x)dx& =& \underset{u=a}{\overset{0}{\int }}f(u)(-du)\\ & =& -\underset{u=a}{\overset{0}{\int }}f(u)du\\ & =& \underset{u=0}{\overset{a}{\int }}f(u)du\end{array}$

Berdasarkan uraian di atas, dapat disimpulkan bahwa ∫−a0f(x)dx=∫0af(x)dx$\underset{-a}{\overset{0}{\int }}f(x)dx=\underset{0}{\overset{a}{\int }}f(x)dx$.

Dengan demikian,

∫−aaf(x)dx===∫−a0f(x)dx+∫0af(x)dx∫0af(x)dx+∫0af(x)dx2∫0af(x)dx$\begin{array}{lll}\underset{-a}{\overset{a}{\int }}f(x)dx& =& \underset{-a}{\overset{0}{\int }}f(x)dx+\underset{0}{\overset{a}{\int }}f(x)dx\\ & =\end{array}$

$\begin{array}{l}\underset{0}{\overset{a}{\int }}f(x)dx+\underset{0}{\overset{a}{\int }}f(x)dx\\ & =& 2\underset{0}{\overset{a}{\int }}f(x)dx\end{array}$

Apa yang dapat kamu simpulkan dari uraian di atas?

Tepat sekali. Jika f$f$ adalah fungsi genap dan kontinu pada interval [−a,a]$[-a,a]$, maka ∫−aaf(x)dx=2∫0af(x)dx$\underset{-a}{\overset{a}{\int }}f(x)dx=2\underset{0}{\overset{a}{\int }}f(x)dx$.

Fungsi Ganjil

Fungsi f$f$ merupakan fungsi ganjil jika dan hanya jika untuk sebarang nilai x$x$ pada domain fungsi berlaku persamaan: f(−x)=−f(x)$f(-x)=-f(x)$.

Sebagai ilustrasi, misalkan fungsi f$f$ kontinu pada interval [−a,a]$[-a,a]$, dengan grafik fungsi sebagai berikut:

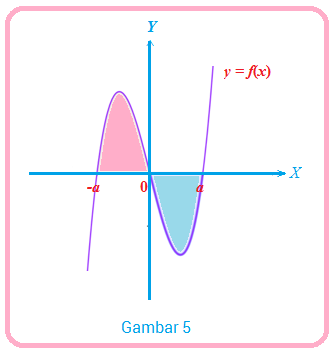
Berdasarkan sifat intergral tentu, luas daerah berwarna pada grafik di atas adalah ∫−aaf(x)dx=∫−a0f(x)dx+∫0af(x)dx$\underset{-a}{\overset{a}{\int }}f(x)dx=\underset{-a}{\overset{0}{\int }}f(x)dx+\underset{0}{\overset{a}{\int }}f(x)dx$.

Nah, jika kita misalkan u=−x$u=-x$, maka

• x=a$x=a$ ⇒ u=−a$u=-a$
• x=0$x=0$ ⇒ u=0$u=0$
• f(x)=f(−u)=−f(u)$f(x)=f(-u)=-f(u)$ → fungsi ganjil
• dudx=d(−x)dx⇔dudx=−1⇔dx=−du$\frac{du}{dx}=\frac{d\left(-x\right)}{dx}\iff \frac{du}{dx}=-1\iff dx=-du$

Akibatnya,

∫x=−a0f(x)dx===∫u=a0−f(u)(−du)∫u=a0f(u)du−∫u=0af(u)du$\begin{array}{lll}\underset{x=-a}{\overset{0}{\int }}f(x)dx& =& \underset{u=a}{\overset{0}{\int }}-f(u)(-du)\\ & =& \underset{u=a}{\overset{0}{\int }}f(u)du\end{array}$

$\begin{array}{lll}& =& -\underset{u=0}{\overset{a}{\int }}f(u)du\end{array}$

Berdasarkan uraian di atas, dapat disimpulkan bahwa ∫−a0f(x)dx=−∫0af(x)dx$\underset{-a}{\overset{0}{\int }}f(x)dx=-\underset{0}{\overset{a}{\int }}f(x)dx$.

Dengan demikian,

∫−aaf(x)dx===∫−a0f(x)dx+∫0af(x)dx−∫0af(x)dx+∫0af(x)dx0$\begin{array}{lll}\underset{-a}{\overset{a}{\int }}f(x)dx& =& \underset{-a}{\overset{0}{\int }}f(x)dx+\underset{0}{\overset{a}{\int }}f(x)dx\end{array}$

$\begin{array}{lll}& =& -\underset{0}{\overset{a}{\int }}f(x)dx+\underset{0}{\overset{a}{\int }}f(x)dx\\ & =& 0\end{array}$

Apa yang dapat kamu simpulkan dari uraian di atas?

Tepat sekali. Jika f$f$ adalah fungsi ganjil dan kontinu pada interval [−a,a]$[-a,a]$, maka ∫−aaf(x)dx=0$\underset{-a}{\overset{a}{\int }}f(x)dx=0$.

Fungsi Periodik

Sebagai ilustrasi, jika dimisalkan f$f$ adalah fungsi periodik dengan periode p$p$, maka f(x+p)=f(x)$f(x+p)=f(x)$.

Selanjutnya, jika dimisalkan fungsi f$f$ tersebut kontinu pada interval [a,b+p]$[a,b+p]$, maka dapat kita gambarkan grafik fungsi periodik sebagai berikut:

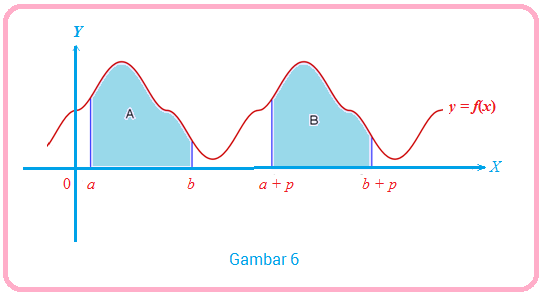
Selajutnya, jika kita misalkan u=x−p$u=x-p$, maka

• x=u+p$x=u+p$
• dx=du$dx=du$
• f(u+p)=f(u)$f(u+p)=f(u)$ → periodenya adalah p$p$

Akibatnya, ∫a+pb+pf(x)dx=∫abf(u+p)du=∫abf(u)du$\underset{a+p}{\overset{b+p}{\int }}f(x)dx=\underset{a}{\overset{b}{\int }}f(u+p)du=\underset{a}{\overset{b}{\int }}f(u)du$.

Apa yang dapat kalian simpulkan dari uraian di atas?

Ya, jika f$f$ merupakan fungsi periodik dengan periode p$p$ dan kontinu pada nterval [a+p,b+p]$[a+p,b+p]$, maka berlaku persamaan ∫a+pb+pf(x)dx=∫abf(x)dx$\underset{a+p}{\overset{b+p}{\int }}f\left(x\right)dx=\underset{a}{\overset{b}{\int }}f\left(x\right)dx$.

Agar kalian semakin paham dengan materi di atas, yuk cermati beberapa contoh soal berikut ini.

Contoh 1: Fungsi Genap

Tentukan nilai dari ∫−22(−x2+4)dx$\underset{-2}{\overset{2}{\int }}(-x^2+4)dx$.

Penyelesaian:

Oleh karena f(−x)=−(−x)2+4=−x2+4$f\left(-x\right)=-{\left(-x\right)}^2+4=-x^2+4$, maka fungsi f(x)=−x2+4$f(x)=-x^2+4$merupakan fungsi genap.

Dengan demikian,

∫−22(−x2+4)dx======2∫02(−x2+4)dx∫02(−2x2+8)dx[−23x3+8x]20−23(8)+16−163+16323$\begin{array}{lll}\underset{-2}{\overset{2}{\int }}(-x^2+4)dx& =& 2\underset{0}{\overset{2}{\int }}(-x^2+4)dx\\ & =& \underset{0}{\overset{2}{\int }}\end{array}$

$\begin{array}{l}(-2x^2+8)dx\\ & =& {\left[-\frac{2}{3}{x}^3+8x\right]}_0^2\\ & =& -\frac{2}{3}\left(8\right)+16\\ & =& -\frac{16}{3}+16\\ & =& \frac{32}{3}\end{array}$

Contoh 2: Fungsi Ganjil

Tentukan nilai dari ∫−11(x5−2x3)dx$\underset{-1}{\overset{1}{\int }}(x^5-2x^3)dx$.

Penyelesaian:

Oleh karena f(−x)=(−x)5−2(−x)3=−x5+2x3=−(x5−2x3)$f\left(-x\right)={\left(-x\right)}^5-2{\left(-x\right)}^{}$

$3^{}=-x^5+2x^3=-\left(x^5-2x^3\right)$, maka fungsi f(x)=x5−2x3$f(x)=x^5-2x^3$ merupakan fungsi ganjil.

Dengan demikian, ∫−11(x5−2x3)dx=0$\underset{-1}{\overset{1}{\int }}(x^5-2x^3)dx=0$.

Contoh 3: Fungsi Periodik

Tentukan nilai dari ∫02π|sinx|dx$\underset{0}{\overset{2\pi }{\int }}\left|\sin x\right|dx$.

Penyelesaian:

Oleh karena periode dari fungsi f(x)=|sinx|$f\left(x\right)=\left|\sin x\right|$ adalah π$\pi$, maka

∫02π|sinx|dx========∫0π|sinx|dx+∫0+ππ+π|sinx|dx∫0π|sinx|dx+∫0π|sinx|dx2∫0πsinxdx2[−cosx]π02(−cosπ−(−cos0))2(1−(−1))2(2)4$\begin{array}{l}\underset{}{\overset{}{<br>}}\end{array}$

$\begin{array}{lll}\underset{0}{\overset{2\pi }{\int }}\left|\sin x\right|dx& =& \underset{0}{\overset{\pi }{\int }}\left|\sin x\right|dx+\underset{0+\pi }{\overset{\pi +\pi }{\int }}\left|\sin x\right|dx\\ & =& \underset{0}{\overset{\pi }{\int }}\left|\sin x\right|dx+\underset{0}{\overset{\pi }{\int }}\left|\sin x\right|dx\\ & =& 2\underset{0}{\overset{\pi }{\int }}\sin xdx\\ & =& 2\end{array}$

$\begin{array}{l}{\left[-\cos x\right]}_0^{\pi }\\ & =& 2\left(-\cos \pi -\left(-\cos 0\right)\right)\\ & =& 2\left(1-\left(-1\right)\right)\\ & =& 2\left(2\right)\\ & =& 4\end{array}$

Penjelasan pada materi dan contoh soal di atas mudah dipahami bukan?

Yuk kerjakan latihan soal yang ada dalam topik ini.