Komposisi Dua Rotasi Berurutan yang Sepusat

Komposisi Dua Rotasi Berurutan yang Sepusat - Pada topik sebelumnya, kalian telah belajar mengenai transformasi geometri berupa rotasi. Nah, dalam topik ini kalian akan belajar tentang komposisi dua rotasi berurutan dengan titik pusat sama.

Apakah kalian masih ingat dengan definisi rotasi?

Ya, rotasi atau perputaran adalah bentuk transformasi geometri yang memindahkan suatu titik atau objek dengan cara memutar semua titik pada objek tersebut dalam satu bidang terhadap suatu titik pusat (poros) tertentu dengan arah dan sudut rotasi yang besarnya tertentu pula.

Arah putaran sudut rotasi bernilai negatif jika arah arah putaran tersebut searah dengan arah putaran jarum jam dan bernilai positif jika arah putaran tersebut berlawanan arah dengan arah putaran jarum jam.

Dalam kehidupan sehari-hari, rotasi sering kita temui. Sebagai contoh, roda kendaraan yang berputar saat kalian mengendarai sepeda motor.

Yuk kita perhatikan ilustrasi mengenai rotasi berikut.

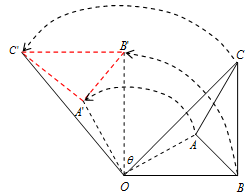
Pada ilustrasi di atas, ∆ABC$∆ABC$ dirotasi sejauh θ$\theta$ dengan arah rotasi adalah berlawanan arah dengan arah putar jarum jam dan titik pusat rotasi adalah O(0,0)$O(0,0)$. Nah, ∆A′B′C′$∆A^{\prime }{B}^{\prime }{C}^{\prime }$terhadap rotasi tersebut.

Seperti yang telah kalian pelajari sebelumnya, persamaan matriks untuk menentukan bayangan titik (x,y)$(x,y)$ terhadap rotasi sejauh θ$\theta$ dengan titik pusat rotasi O(0,0)$O(0,0)$ adalah

(x′y′)=(cosθsinθ−sinθcosθ)(xy)$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{cc}\mathrm{c}\mathrm{o}\mathrm{s}\theta & -\mathrm{s}\mathrm{i}\mathrm{n}\theta \\ \mathrm{s}\mathrm{i}\mathrm{n}\theta & \mathrm{c}\mathrm{o}\mathrm{s}\theta \end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)$

dengan (x′,y′)$(x^{\prime },y^{\prime })$ adalah koordinat titik bayangan.

Adapun persamaan matriks untuk menentukan bayangan titik (x,y)$(x,y)$ terhadap rotasi sejauh θ$\theta$ dengan titik pusat rotasi (a,b)$(a,b)$ adalah

(x′y′ )=(cosθsinθ−sinθcosθ )(x−ay−b )+(ab )


$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{cc}\text{cos}\theta & -\text{sin}\theta \\ \text{sin}\theta & \text{cos}\theta \end{array}\right)$

$\left(\begin{array}{c}x-a\\ y-b\end{array}\right)+\left(\begin{array}{c}a\\ b\end{array}\right)$

dengan (x′,y′)$(x^{\prime },y^{\prime })$ adalah koordinat titik bayangan.

Tahukah kalian bagaimana cara menentukan bayangan suatu titik dari dua rotasi yang berurutan?

Yuk kita temukan jawabannya dalam pembahasan berikut.

Komposisi Dua Rotasi

Seperti yang telah kalian ketahui, jika fungsi f$f$ dikomposisikan dengan fungsi g$g$, maka hasil komposisi kedua fungsi dinyatakan dengan notasi f∘g$f\circ g$ atau g∘f$g\circ f$, tergantung mana fungsi yang dioperasikan dahulu.

Nah, dalam topik ini kita hanya akan membahas komposisi dua rotasi dengan titik pusat rotasi yang sama.

Yuk perhatikan ilustrasi berikut.

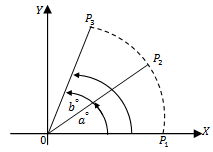
Pada ilustrasi di atas, titik P1$P_1$ dirotasi sebesar a°$a°$ terhadap titik pusat O(0,0)$O(0,0)$, kemudian dirotasi lagi sebesar b°$b°$ terhadap titik pusat yang sama. Adapun hasil rotasi tersebut adalah titik P3$P_3$.

Jika kalian perhatikan kembali ilustrasi di atas, tampak bahwa hasil rotasi dari titik P1$P_1$terhadap dua rotasi berurutan sama dengan hasil rotasi titik P1$P_1$ terhadap rotasi sebesar (a°+b°)$(a°+b°)$.

Agar kalian semakin paham dengan penjelasan di atas, yuk kita cermati beberapa contoh soal berikut.

Contoh

Titik Z(2,3)$Z(2,3)$ dirotasi sejauh 30°$30°$ dengan titik pusat rotasi O(0,0)$O(0,0)$ dan arah rotasi berlawanan arah dengan arah putar jarum jam. Selanjutnya bayangan dari titik tersebut dirotasi sejauh 90°$90°$ dengan titik pusat rotasi O(0,0)$O(0,0)$ dan arah rotasi berlawanan arah dengan arah putar jarum jam. Tentukan koordinat titik bayangannya.

Penyelesaian:

Oleh karena arah rotasi berlawanan arah dengan arah putar jarum jam, maka besar sudut rotasi bernilai positif.

Selanjutnya, karena pusat rotasi adalah sama, maka dua rotasi dalam soal di atas dapat dikomposisikan, dimana besar sudut rotasi adalah 30°+90°=120°$30°+90°=120°$.

Dengan demikian, bayangan titik Z(2,3)$Z(2,3)$ dapat ditentukan dengan cara sebagai berikut:

(x′y′ )===(cos120°sin120°−sin120°cos120° )(xy )(−12123‾√−123‾√−12 )(32 )(−32−3‾√323‾√−1 ) $\begin{array}{l}<br>\end{array}$

$\begin{array}{lll}\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)& =& \left(\begin{array}{cc}\cos 120°& -\sin 120°\\ \sin 120°& \cos 120°\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)\\ & =& \left(\begin{array}{cc}-\frac{1}{2}& -\frac{1}{2}\sqrt{3}\\ \frac{1}{2}\sqrt{3}& -\frac{1}{2}\end{array}\right)\left(\begin{array}{c}3\\ 2\end{array}\right)\\ & =& \left(\begin{array}{c}-\frac{3}{2}-\sqrt{3}\\ \frac{3}{2}\sqrt{3}-1\end{array}\right)\end{array}$

Berdasarkan uraian di atas, dapat disimpulkan bahwa bayangan titik Z(2,3)$Z(2,3)$ adalah Z′(−32−3‾√,323‾√−1)$Z^{\prime }(-\frac{3}{2}-\sqrt{3},\frac{3}{2}\sqrt{3}-1)$.