Refleksi terhadap Dua Sumbu yang Sejajar dengan Sumbu Y

Refleksi terhadap Dua Sumbu yang Sejajar dengan Sumbu Y - Pada topik sebelumnya kalian telah belajar tentang komposisi transformasi refleksi terhadap garis 

y=a$y=a$ yang dilanjutkan dengan refleksi terhadap garis y=b$y=b$. Nah, dalam topik kali ini, kalian akan belajar tentang komposisi transformasi refleksi terhadap garis x=h$x=h$ yang dilanjutkan dengan refleksi terhadap garis x=k$x=k$.

Yuk kita cari tahu perbedaan kedua transformasi tersebut dalam topik ini.

Konsep Dasar

Apakah kalian masih ingat dengan hasil refleksi titik (x,y)$(x,y)$ oleh refleksi terhadap garis x=a$x=a$?

Ya, hasil refleksi titik (x,y)$(x,y)$ oleh refleksi terhadap garis x=a$x=a$ adalah titik (2a−x,y)$(2a-x,y)$.

Nah, berdasarkan rumus tersebut, dapat kita simpulkan bahwa:

• bayangan titik (x,y)$(x,y)$ oleh refleksi terhadap garis x=h$x=h$ adalah titik (2h−x,y)$(2h-x,y)$
• bayangan titik (2h−x,y)$(2h-x,y)$ oleh refleksi terhadap garis x=k$x=k$ adalah titik (2k−(2h−x),y=(x+2(k−h),y)$(2k-(2h-x),y=(x+2(k-h),y)$

Dengan demikian, bayangan titik (x,y)$(x,y)$ oleh refleksi terhadap garis x=h$x=h$ dilanjutkan dengan refleksi garis x=k$x=k$ adalah titik (x+2(k−h),y)$(x+2(k-h),y)$.

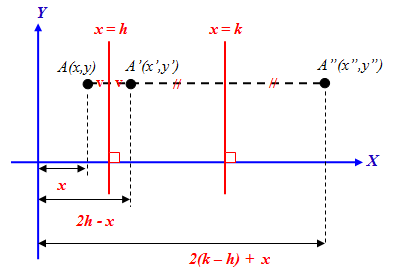
Tahukah kalian bagaimana bentuk persamaan matriks dari transformasi tersebut?

Ya, oleh karena koordinat titik bayangan adalah (x″,y″)=(x+2(k−h),y)$(x^{″},y^{″})=(x+2(k-h),y)$, maka bentuk persamaan matriksnya adalah sebagai berikut:

(x″y″)=(xy)+(2(k−h)0)$\left(\begin{array}{l}{x}^{″}\\ y^{″}\end{array}\right)=\left(\begin{array}{l}x\\ y\end{array}\right)+\left(\begin{array}{l}2\left(k-h\right)\\ 0\end{array}\right)$

Agar kalian semakin paham dengan materi di atas, yuk kita cermati beberapa contoh berikut.

Contoh 1

Tentukan bayangan titik (3,9)$(3,9)$ oleh refleksi terhadap garis x=4$x=4$ dilanjutkan dengan refleksi terhadap garis x=6$x=6$.

Penyelesaian:

Soal di atas dapat diselesaikan dengan dua cara, yaitu penyelesaian dengan geometri analitik dan penyelesaian dengan menggunakan persamaan matriks.

Geometri Analitik

Oleh karena refleksi pertama adalah terhadap garis x=4$x=4$, maka h=4$h=4$.

Selanjutnya, karena refleksi kedua adalah terhadap garis x=6$x=6$, maka k=6$k=6$.

Nah, karena bayangan titik (x,y)$(x,y)$ oleh refleksi terhadap garis x=h$x=h$ dilanjutkan dengan refleksi garis x=k$x=k$ adalah titik (x+2(k−h),y)$(x+2(k-h),y)$, maka bayangan titik (3,9)$(3,9)$ terhadap transformasi dalam soal adalah titik (3+2(6−4),9)=(3+4,9)=(7,9)$(3+2(6-4),9)=(3+4,9)=(7,9)$.

Persamaan Matriks

Jika dimisalkan bayangan titik (x,y)$(x,y)$ terhadap transformasi dalam soal adalah (x′,y′)$(x^{\prime },y^{\prime })$, maka

(x′y′)====(xy)+(2(k−h)0)(39)+(2(6−4)0)(39)+(40)(79)$\begin{array}{lll}\left(\begin{array}{l}{x}^{\prime }\\ y^{\prime }\end{array}\right)& =& \left(\begin{array}{l}x\\ y\end{array}\right)+\left(\begin{array}{l}2\left(k-h\right)\\ 0\end{array}\right)\\ & =& \left(\begin{array}{l}3\\ 9\end{array}\right)+\left(\begin{array}{l}2\left(6-4\right)\\ 0\end{array}\right)\\ & =& \left(\begin{array}{l}3\\ 9\end{array}\right)+\left(\begin{array}{l}4\\ 0\end{array}\right)\\ & =& \left(\begin{array}{l}7\\ 9\end{array}\right)\end{array}$

Berdasarkan uraian di atas, dapat disimpulkan bahwa bayangan titik (3,9)$(3,9)$ adalah titik (7,9)$(7,9)$.

Nah, apakah kalian bagaimana cara menentukan bayangan suatu titik oleh refleksi berurutan terhadap dua garis yang sejajar dengan sumbu Y$Y$?

Yuk kita temukan jawabannya dengan mencermati contoh berikut ini.

Contoh 2

Tentukan bayangan garis y=5x−1$y=5x-1$ oleh refleksi terhadap garis x=2$x=2$ dilanjutkan dengan refleksi terhadap garis x=6$x=6$.

Penyelesaian:

Soal di atas dapat diselesaikan dalam tiga langkah, yaitu

1. Memisalkan bayangan titik (x,y)$(x,y)$ adalah titik (x′,y′)$(x^{\prime },y^{\prime })$.
2. Menentukan hubungan antara variabel x$x$ dan x′$x^{\prime }$, serta hubungan antara variabel y$y$dan y′$y^{\prime }$.
3. Mensubtitusikan variabel x$x$ dan y$y$ ke persamaan garis.

Yuk kita cermati pembahasan berikut ini.

Oleh karena bayangan titik (x,y)$(x,y)$ oleh transformasi dalam soal adalah (x′,y′)$(x^{\prime },y^{\prime })$, maka kita peroleh hubungan sebagai berikut:

(x′y′)⇔(x′y′)⇔(x′y′)⇔(xy)====(xy)+(2(k−h)0)(xy)+(2(6−2)0)(xy)+(80)(x′−8y′)$\begin{array}{l}<br>\end{array}$

$\begin{array}{lll}\left(\begin{array}{l}{x}^{\prime }\\ y^{\prime }\end{array}\right)& =& \left(\begin{array}{l}x\\ y\end{array}\right)+\left(\begin{array}{l}2\left(k-h\right)\\ 0\end{array}\right)\\ \iff \left(\begin{array}{l}{x}^{\prime }\\ y^{\prime }\end{array}\right)& =& \left(\begin{array}{l}x\\ y\end{array}\right)+\left(\begin{array}{l}2\left(6-2\right)\\ 0\end{array}\right)\\ \iff \left(\begin{array}{l}{x}^{\prime }\\ y^{\prime }\end{array}\right)& =& \left(\begin{array}{l}x\\ y\end{array}\right)+\left(\begin{array}{l}8\\ 0\end{array}\right)\\ \iff \left(\begin{array}{l}x\\ y\end{array}\right)& =& \left(\begin{array}{l}{x}^{\prime }-8\\ y^{\prime }\end{array}\right)\end{array}$

Nah, jika kita subtitusikan x′=x$x^{\prime }=x$ dan y=y′$y=y^{\prime }$ ke persamaan garis y=5x−1$y=5x-1$, maka akan kita peroleh persamaan garis bayangan sebagai berikut:

y⇔y′⇔y′===5x−15(x′−8)−15x′−41$\begin{array}{lll}y& =& 5x-1\\ \iff y^{\prime }& =& 5\left(x^{\prime }-8\right)-1\\ \iff y^{\prime }& =& 5x^{\prime }-41\end{array}$

Jadi, bayangan garis y=5x−1$y=5x-1$ oleh refleksi terhadap garis x=2$x=2$ dilanjutkan dengan refleksi terhadap garis x=6$x=6$ adalah y=5x−41$y=5x-41$.

Yuk kerjakan sepuluh latihan soal dalam topik ini untuk menguji pemahaman kalian.