Menghitung Volume Benda Jika Luas Irisan Bidang Diketahui

Menghitung Volume Benda Jika Luas Irisan Bidang Diketahui - Pada topik sebelumnya, kalian telah belajar tentang bagaimana menghitung luas suatu daerah dengan menggunakan integral tentu. Nah, dalam topik ini kalian akan belajar tentang bagaimana menentukan volume suatu benda jika luas daerah irisannya diketahui.

Secara umum, volume suatu benda (V)$(V)$ adalah perkalian antara luas alas (A)$(A)$ dan tinggi benda tersebut (t)$(t)$ → V=At$V=At$.

Lebih lanjut, volume sebuah benda padat M$M$ dengan irisan bidang tegak lurus sumbu X$X$dan luas daerah irisan A(x)$A(x)$ pada interval [a,b]$[a,b]$ adalah VM=∫abA(x)dx$V_M=\underset{a}{\overset{b}{\int }}A(x)dx$.

Apakah kalian sudah paham dengan materi di atas?

Agar kalian semakin paham, yuk kita cermati beberapa contoh berikut ini.

Contoh 1

Alas sebuah benda terletak pada daerah bidang datar yang dibatasi oleh sumbu X$X$, sumbu Y$Y$, garis x=4$x=4$, dan garis y=2$y=2$. Jika setiap irisan tipis yang tegak lurus terhadap sumbu X$X$ berbentuk persegi, maka berapakah volume benda tersebut?

Penyelesaian:

Berdasarkan informasi dalam soal, sketsa bidang alas dari benda yang dimaksud adalah sebagai berikut:

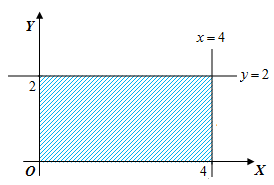
Adapun sketsa benda dalam dimensi tiga adalah sebagai berikut:

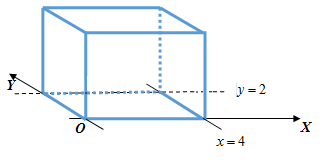
Oleh karena setiap irisan tipis pada benda tersebut berbentuk persegi dan tegak lurus dengan sumbu X$X$, maka tinggi benda sama dengan lebar benda, yaitu s=2$s=2$ satuan panjang.

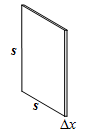
Selanjutnya, dengan memisalkan tebal setiap irisan adalah ∆x$∆x$, maka volume irisan tipis tersebut adalah ΔV=A(x)Δx=s2Δx=4Δx$\mathrm{\Delta }V=A\left(x\right)\mathrm{\Delta }x=s^2\mathrm{\Delta }x=4\mathrm{\Delta }x$ satuan luas.

Nah, karena jumlah dari semua volume irisan tipis tersebut adalah volume dari benda yang dimaksud, maka volume benda adalah V=∫044dx=[4x]40=16$V=\underset{0}{\overset{4}{\int }}4dx={\left[4x\right]}_0^4=16$ satuan volume.

Pada contoh di atas, sebenarnya benda yang dimaksud adalah sebuah balok dengan panjang 4 satuan, lebar 2 satuan, dan tinggi 2 satuan.

Tanpa menggunakan integral tentupun kalian pasti dapat menghitung volume benda tersebut. Penggunaan integral tentu justru terasa lebih rumit.

Yuk kita cermati bagaimana penggunaan integral tentu dalam perhitungan yang lebih sulit.

Contoh 2

Alas sebuah benda terletak pada daerah bidang datar yang dibatasi oleh sumbu X$X$, sumbu Y$Y$, garis x=5$x=5$, dan garis 2x−5y+5=0$2x-5y+5=0$. Jika setiap irisan tipis yang tegak lurus terhadap sumbu X$X$ berbentuk persegi, maka berapakah volume benda tersebut?

Penyelesaian:

Berdasarkan informasi dalam soal, sketsa bidang alas dari benda yang dimaksud adalah sebagai berikut:

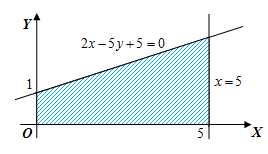
Adapun sketsa benda dalam dimensi tiga adalah sebagai berikut:

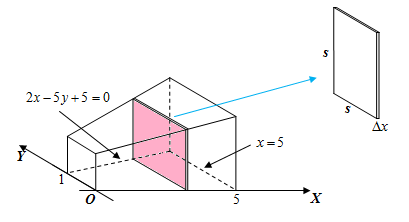
Oleh karena setiap irisan tipis pada benda tersebut berbentuk persegi dan tegak lurus dengan sumbu X$X$, maka tinggi benda sama dengan lebar benda, yaitu s=25x+1$s=\frac{2}{5}x+1$satuan panjang.

Selanjutnya, dengan memisalkan tebal setiap irisan adalah ∆x$∆x$, maka volume irisan tipis tersebut adalah

ΔV====A(x)Δxs2Δx(25x+1)2Δx(425x2+45x+1)Δx$\begin{array}{lll}\mathrm{\Delta }V& =& A\left(x\right)\mathrm{\Delta }x\\ & =& s^2\mathrm{\Delta }x\\ & =& {\left(\frac{2}{5}x+1\right)}^2\mathrm{\Delta }x\\ & =& \left(\frac{4}{25}{x}^2+\frac{4}{5}x+1\right)\mathrm{\Delta }x\end{array}$

Nah, karena jumlah dari semua volume irisan tipis tersebut adalah volume dari benda yang dimaksud, maka

V=====∫05(425x2+45x+1)dx[475x3+410x2+x]50475(5)3+25(5)2+5203+10+5653$\begin{array}{lll}V& =& \underset{0}{\overset{5}{\int }}\left(\frac{4}{25}{x}^2+\frac{4}{5}x+1\right)dx\\ & =& {\left[\frac{4}{75}{x}^3+\frac{4}{10}{x}^2+x\right]}_0^5\\ & =& \frac{4}{75}\end{array}$

$\begin{array}{l}{\left(5\right)}^3+\frac{2}{5}{\left(5\right)}^2+5\\ & =& \frac{20}{3}+10+5\\ & =& \frac{65}{3}\end{array}$

Jadi, volume benda yang dimaksud adalah 653$\frac{65}{3}$ satuan volume.

Nah, pada contoh 2 di atas kalian dapat melihat bagaimana peranan integral tentu dalam menentukan volume suatu benda.

Yuk kita perhatikan contoh selanjutnya.

Contoh 3

Sebuah limas segi empat beraturan memiliki panjang sisi alas M$M$ satuan dan tinggi limas T$T$ satuan. Dengan menggunakan integral tentu, buktikan bahwa volume limas tersebut adalah V=13M2T$V=\frac{1}{3}{M}^{2}T$ satuan volume.

Bukti:

Berdasarkan informasi dalam soal, dapat kita buat sketsa sebagai berikut:

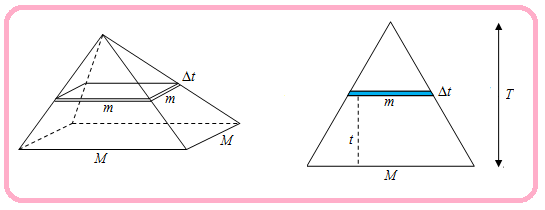
Pada sketsa di atas, tampak bahwa irisan tipis berbentuk persegi dengan panjang sisi m$m$dan ketebalan ∆t$∆t$ saling bertumpuk membentuk limas.

Berdasarkan konsep kesebangunan, kita ketahui bahwa mM=T−tT⇔m=(T−tT)M$\frac{m}{M}=\frac{T-t}{T}\iff m=\left(\frac{T-t}{T}\right)M$.

Dengan demikian, volume irisan tipis pada sketsa di atas adalah

ΔV====A(t)Δtm2Δt((T−tT)M)2ΔtM2T2(T2−2Tt+t2)Δt$\begin{array}{lll}\mathrm{\Delta }V& =& A\left(t\right)\mathrm{\Delta }t\\ & =& m^2\mathrm{\Delta }t\\ & =& {\left(\left(\frac{T-t}{T}\right)M\right)}^2\mathrm{\Delta }t\\ & =& \frac{M^2}{T^2}\left(T^2-2Tt+t^2\right)\mathrm{\Delta }t\end{array}$

Nah, karena jumlah dari semua volume irisan tipis tersebut adalah volume dari benda yang dimaksud, maka

V=====∫0T(M2T2(T2−2Tt+t2))dtM2T2[T2t−Tt2+13t3]T0M2T2(T2(T)−T(T)2+13(T)3)M2T2(T3−T3+13T3)13M2T$\begin{array}{lll}V& =& \underset{0}{\overset{T}{\int }}\left(\frac{M^2}{T^2}\left(T^2-2Tt+t^2\right)\right)dt\\ & =& \frac{M^2}{T^2}{[T^{2}t-T{t}^2+}_{}^{}\end{array}$

$\begin{array}{l}{\frac{1}{3}{t}^3]}_0^T\\ & =& \frac{M^2}{T^2}\left(T^2\left(T\right)-T{\left(T\right)}^2+\frac{1}{3}{\left(T\right)}^3\right)\\ & =& \frac{M^2}{T^2}\left(T^3-T^3+\frac{1}{3}{T}^3\right)\\ & =& \frac{1}{3}{M}^{2}T\end{array}$

Berdasarkan uraian di atas, terbukti bahwa volume limas segi empat beraturan dengan panjang sisi alas M$M$ satuan dan tinggi limas T$T$ satuan adalah V=13M2T$V=\frac{1}{3}{M}^{2}T$ satuan volume.

Nah, untuk menguji pemahaman kalian, yuk kerjakan sepuluh latihan soal dalam topik ini.