Refleksi terhadap Garis y = x

Refleksi terhadap Garis y = x - Pada topik sebelumnya, kalian telah belajar mengenai refleksi terhadap garis sumbu X dan Y. Nah, pada topik ini kalian akan belajar tentang refleksi terhadap garis y = x.

Kalian tentu masih ingat bagaimana cara menggambar garis y = x bukan?

Saya yakin kalian pasti masih ingat.

Konsep Dasar

Untuk memudahkan pemahaman kalian mengenai konsep refleksi terhadap garis y = x, mari kita perhatikan gambar berikut.

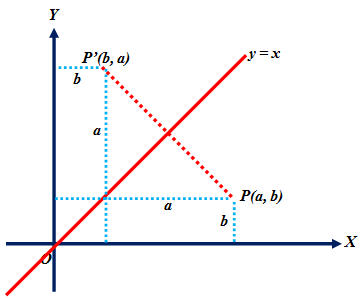
Pada gambar di atas, tampak bahwa bayangan titik P(a, b) jika direfleksikan terhadap garis y = x adalah titik P’(b, a).

Dengan demikian, dapat kita simpulkan bahwa bayangan titik (x, y) oleh refleksi terhadap garis y = x adalah (x' , y') = (y, x).

Selanjutnya, karena

• x’ = y = (0)x + (1)y
• y’ = x = (1)x + (0)y

maka kita peroleh persamaan matriks sebagai berikut: (x′y′ )=(0110 )(xy )$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)$.

Pada persamaan matriks tersebut, tampak bahwa matriks transformasi refleksi terhadap garis y = x adalah (0110 )$\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)$.

Nah, untuk membantu pemahaman kalian, mari kita perhatikan contoh berikut.

Contoh 1:

Tentukan bayangan titik A(3, -7) dan B(-5, 2) jika direfleksikan terhadap garis y = x.

Penyelesaian:

Jika X adalah matriks hasil transformasi, maka

X$X$

=(0110 )(3−7−52 )$=\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)\left(\begin{array}{ll}3& -5\\ -7& 2\end{array}\right)$

=(−732−5 )$=\left(\begin{array}{ll}-7& 2\\ 3& -5\end{array}\right)$

Dengan demikian, bayangan titik A(3, -7) dan B(-5, 2) oleh refleksi terhadap garis y = xadalah A(-7, 3) dan B(2, -5).

Bagaimana jika sebuah garis direfleksikan terhadap garis y = x?

Tentu bayangannya tetap merupakan garis.

Mari kita buktikan melalui contoh berikut.

Contoh 2:

Tentukan bayangan garis y = 3x – 5 jika direfleksikan terhadap garis y = x.

Penyelesaian:

Jika (x', y') adalah koordinat titik bayangan dari titik (x, y) oleh refleksi terhadap garis y = x, maka berdasarkan eliminasi Gauss-Jordan (menukar baris kedua dengan baris pertama) kita peroleh hasil sebagai berikut:

(0110 ∣∣∣x′y′ )$(\begin{array}{cc}0& 1\\ 1& 0\end{array}|\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array})$ R2↔R1$R_2\leftrightarrow R_1$ (1001 ∣∣∣y′x′ )$(\begin{array}{cc}1& 0\\ 0& 1\end{array}|\begin{array}{c}{y}^{\prime }\\ x^{\prime }\end{array})$

Berdasarkan bentuk di atas, dapat kita simpulkan bahwa x = y' dan y = x'.

Jika kita subtitusikan variabel x dan y ke dalam persamaan garis y = 3x – 5, maka kita peroleh hasil sebagai berikut:

y=3x−5⇔x′=3y′−5⇔3y′=x′+5  $\begin{array}{rl}& y=3x-5\\ & \iff x^{\prime }=3y^{\prime }-5\\ & \iff 3y^{\prime }=x^{\prime }+5\end{array}$

Dengan demikian, bayangan garis y = 3x – 5 oleh refleksi garis y = x adalah 3y = x + 5.

Materi ini mudah bukan?

Uji pemahaman kalian dengan mengerjakan latihan soal dalam topik ini.