- Hiperbola Hiperbola adalah tempat kedudukan titik-titik yang selisih jaraknya terhadap dua titik tertentu selalu tetap. Dua titik tertentu itu disebut fokus hiperbola. Contoh persamaan hiperbola adalah
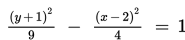
Persamaan hiperbola ini memiliki sumbu utama yang sejajar dengan sumbu y. Rumus bakunya adalah
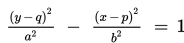
Jadi, a2 = 9 dan b2 = 4 . Akibatnya, c2 = a2 + b2 = 9 + 4 = 13.
Titik pusat hiperbola adalah (2, -1).
Titik puncaknya adalah (2, -1 + 3) = (2, 2) dan (2, -1 – 3) = (2, -4).
Titik fokusnya adalah
Titik pusat hiperbola adalah (2, -1).
Titik puncaknya adalah (2, -1 + 3) = (2, 2) dan (2, -1 – 3) = (2, -4).
Titik fokusnya adalah
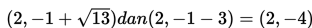
Jika ada garis yang menyinggung hiperbola pada titik R(x1, y1) yang terletak pada hiperbola itu, maka persamaan umum garis singgungnya adalah
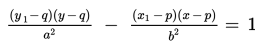
Jika garis yang menyinggung hiperbola itu diketahui gradiennya m, maka persamaan umum garis singgungnya adalah
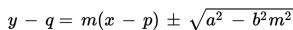
Apakah kalian sudah ingat kembali?
- Penerapan Hiperbola Persamaan hiperbola dan persamaan garis singgungnya dapat diterapkan dalam menyelesaikan masalah nyata seperti pada contoh berikut. Contoh: Ketika mengajar tentang materi jagat raya, Pak Bima Sakti mengajak siswa-siswanya untuk memeragakan model-model benda langit di laboratorium IPA. Dalam peragaan ini, ia menjelaskan bahwa ada suatu komet yang mengitari matahari dengan lintasan berbentuk hiperbola. Matahari adalah salah satu titik fokusnya. Ia membuat model lintasan itu dengan persamaan 2116x2 – 400y2 = 846400. Menurutmu seberapa dekatkah komet itu dengan matahari? Penyelesaian: Untuk memudahkan menyelesaikan masalah ini, kita dapat menggunakan gambar berikut.
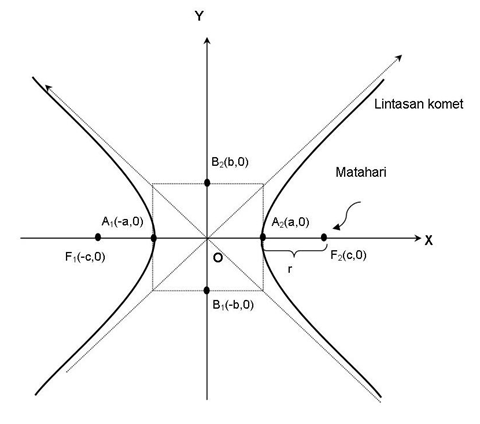
Dalam permasalahan ini, pada dasarnya kita diminta untuk menentukan jarak antara titik fokus dengan titik puncak hiperbola, yaitu r.
Mari kita selesaikan.
Mari kita selesaikan.

Jadi, a = 20 dan b = 46, sehingga c2 = 400 + 2116 => c = 50
Jarak model komet ke model matahari adalah r = 50 – 20 = 30.
Jarak model komet ke model matahari adalah r = 50 – 20 = 30.