Pemecahan masalah nyata tentang dua lingkaran yang saling beririsan

Pemecahan masalah nyata tentang dua lingkaran yang saling beririsan - Jam dinding, ban mobil, dan mata uang logam merupakan beberapa contoh benda-benda yang memiliki bentuk dasar lingkaran. Pada bab sebelumnya, kalian telah mempelajari dan mengenal tentang irisan kerucut yang terdiri atas kurva-kurva parabola, elips dan hiperbola. 

Namun dalam bentuk-bentuknya yang istimewa kita juga akan memperoleh sebuah lingkaran pada irisan kerucut. Pada irisan kerucut, lingkaran terbentuk karena bidang datar mengiris seluruh bagian dari salah satu selimut kerucut dan tegak lurus sumbu kerucut.

Mari kita ingat kembali pengertian lingkaran. Lingkaran adalah himpunan titik-titik yang berjarak sama terhadap suatu titik tertentu. Selain itu tentunya anda juga telah mempelajari topik tentang kedudukan dua lingkaran. Untuk menyegarkan ingatan anda tentang topik tersebut, silahkan perhatikan uraian materi berikut ini.

1. Kedudukan dua lingkaran

Misalkan M1M2 merupakan jarak antara dua pusat lingkaran dan r1 dan r2 merupakan jari-jari kedua lingkaran, maka berlaku :

Dua lingkaran dikatakan berpotongan jika jarak antara kedua titik pusat lingkaran 
M1M2 < r1 + r2

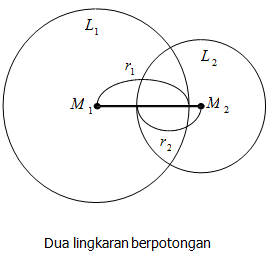
Dua lingkaran dikatakan bersinggungan luar jika jarak antara kedua titik pusat lingkaran M1M2 = r1 + r2

Dua lingkaran dikatakan bersinggungan dalam jika jarak antara kedua titik pusat lingkaran M1M2 = |r1 - r2|

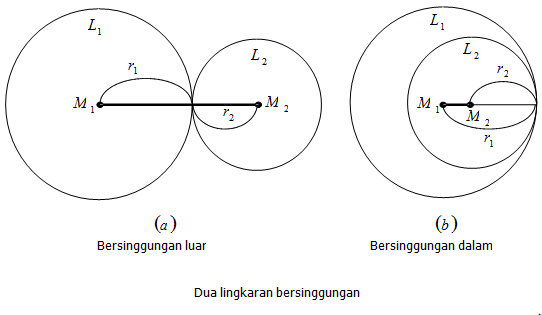
Dua lingkaran dikatakan tidak bersinggungan luar jika jarak antara kedua titik pusat lingkaran M1M2 > r1 + r2

Dua lingkaran dikatakan tidak bersinggungan dalam jika jarak antara kedua titik pusat lingkaran adalah nol (M1M2 = 0 -> M1 = M2) dan r2 > r1

Namun perlu diketahui juga, dua lingkaran dapat tidak bersinggungan dalam jika salah satu lingkaran berada di dalam lingkaran yang lain, M1 ≠ M2 dan r2 > r1

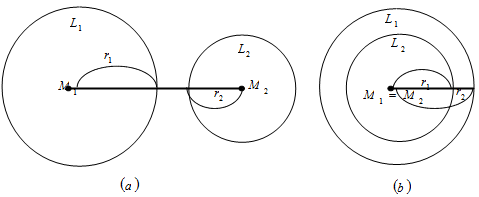
2. Panjang garis singgung persekutuan luar dua lingkaran yang memiliki jari-jari r1 dan r2 dengan r1 > r2, serta jarak kedua pusat lingkaran d adalah :

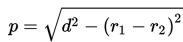
3. Panjang garis singgung persekutuan dalam dua lingkaran yang memiliki jari-jari r1dan r2 serta jarak kedua pusat lingkaran d adalah :

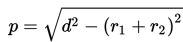
Mari kita cermati beberapa contoh soal berikut ini.

Contoh 1:

Diketahui persamaan lingkaran 
L1 : x2 + y2 + 8x + 6y - 56 = 0 
L2 : x2 + y2 - 8x - 6y - 24 = 0 
Tunjukkan bahwa kedua lingkaran tersebut berpotongan!

Penyelesaian

Syarat dua lingkaran berpotongan adalah jika jarak antara kedua titik pusat lingkaran lebih kecil dari jumlah kedua jari-jari lingkaran. Misalkan M1M2 merupakan jarak antara dua pusat lingkaran dengan r1 dan r2 adalah jari-jari kedua lingkaran, maka M1M2 < r1 + r2

L1 : x2 + y2 + 8x + 6y - 56 = 0
mempunyai pusat M1(-1/2 A , -1/2 B) = (-1/2 (8) , -1/2 (6)) = (-4, -3)
dan

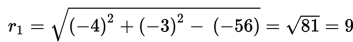
L2 : x2 + y2 - 8x - 6y - 24 = 0

mempunyai pusat M2(-1/2 A , -1/2 B) = (-1/2 (-8) , -1/2 (-6)) = (4,3)
dan

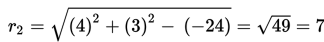
M1M2 merupakan jarak dari (-4 , -3) ke (4,3).

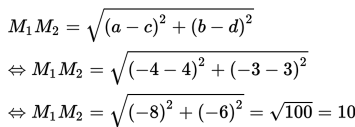
Karena r1 + r2 = 9 + 7 = 16 dan M1M2 = 10, maka M1M2 < r1 + r2.

Dengan demikian, kedua lingkaran berpotongan.

Contoh 2:

Diketahui persamaan lingkaran 
L1 : x2 + y2 + 6x - 4y - 23 = 0 
L2 : x2 + y2 - 12x + 20y + 55 = 0 
Tunjukkan bahwa lingkaran saling bersinggungan di luar!

Penyelesaian

Syarat dua lingkaran bersinggungan di luar adalah
M1M2 = r1 + r2

L1 : x2 + y2 + 6x - 4y - 23 = 0
mempunyai pusat M1(-1/2 A , -1/2 B) = (-1/2 (6) , -1/2 (-4)) = (-3, 2)
dan

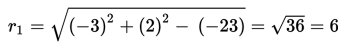
L2 : x2 + y2 - 12x + 20y + 55 = 0

mempunyai pusat M2(-1/2 A , -1/2 B) = (-1/2 (-12) , -1/2 (20)) = (6 , -10)
dan

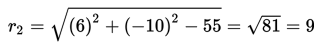
M1M2 merupakan jarak dari (-3 , 2) ke (6 , -10).

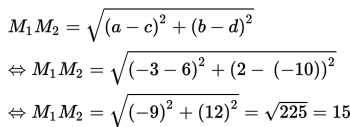
Karena r1 + r2 = 6 + 9 = 15 = M1M2 maka kedua lingkaran bersinggungan di luar.

Contoh 3:

Diketahui persamaan lingkaran 
L1 : x2 + y2 + 20x - 12y + 72 = 0 
L2 : x2 + y2 - 4x - 2y - 11 = 0 
Tunjukkan bahwa kedua lingkaran tidak berpotongan!

Penyelesaian

L1 : x2 + y2 + 6x - 4y - 23 = 0
mempunyai pusat M1(-1/2 A , -1/2 B) = (-1/2 (20) , -1/2 (-12)) = (-10, 6)
dan

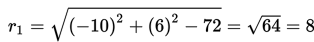
L2 : x2 + y2 - 4x - 2y - 11 = 0

mempunyai pusat M2(-1/2 A , -1/2 B) = (-1/2 (-4) , -1/2 (-2)) = (2,1)
dan

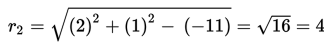
Ada dua jenis lingkaran dikatakan tidak berpotongan, yaitu dua lingkaran tidak berpotongan luar dengan M1M2 > r1 + r2 dan dua lingkaran tidak berpotongan dalam (sepusat / jarak antara dua titik pusat lingkaran (M1M2) adalah nol ⟺ M1 = M2 dan r1 > r2 dan tidak sepusat).

Sekarang, kita akan mengecek titik pusat dari kedua lingkaran tersebut untuk menunjukkan kedua lingkaran tersebut tidak berpotongan luar atau tidak berpotongan dalam.

Titik pusat lingkaran pertama terhadap lingkaran kedua.

Substitusi pusat (-10,6) terhadap lingkaran L2 : x2 + y2 - 4x - 2y - 11 = 0
Syarat titik berada di dalam lingkaran adalah K < 0

Karena
K = (-10)2 + 62 - 4(-10) - 2(6) - 11 = 100 + 36 + 40 - 12 - 11 = 153 > 0 
maka pusat lingkaran pertama berada di luar lingkaran kedua.

Titik pusat lingkaran kedua terhadap lingkaran pertama.

Substitusi pusat (2,1) terhadap lingkaran L1 : x2 + y2 + 20x - 12y + 72 = 0
Syarat titik berada di dalam lingkaran adalah K < 0

Karena
K = 22 + 12 + 20(2) - 12(1) + 72 = 4 + 1 + 40 - 12 + 72 = 103 > 0 
maka pusat lingkaran pertama berada di luar lingkaran pertama.

Jadi , dapat kita simpulkan bahwa kedua lingkaran tidak berpotongan dalam, selanjutnya akan kita tunjukkan bahwa kedua lingkaran tersebut tidak berpotongan luar.

Syarat dua lingkaran tidak berpotongan luar adalah
M1M2 > r1 + r2

M1M2 merupakan jarak dari (-10,6) ke (2,1)

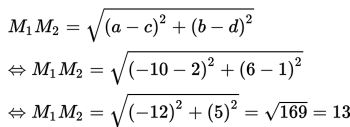
Karena
M1M2 = 13
r1 + r2 = 8 + 4 = 12
maka M1M2 > r1 + r2

Dengan demikian, kedua lingkaran tidak berpotongan di luar.

Contoh 4:

Diketahui jari-jari lingkaran L1 yaitu r1 = 13cm dan jari-jari L2 yaitu r2 = 6cm.

Jika jarak titik pusat kedua lingkaran adalah M1M2 = 25cm, maka tentukan panjang garis singgung persekutuan luar kedua lingkaran tersebut!

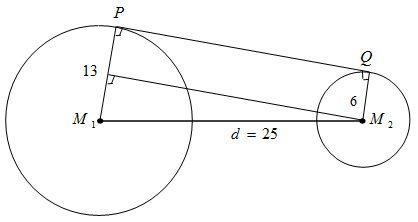
Penyelesaian

Diketahui :
• r1 = 13cm
• r2 = 6cm
• M1M2 = 25cm

Ditanyakan : panjang garis singgung persekutuan luar PQ

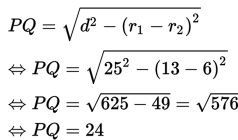
Jadi , panjang garis singgung persekutuan luar kedua lingkaran adalah 24cm.