Pertama, terdapat pasangan aturan untuk fungsi massa peluang.
1. Semua peluang pasti diantara 0 dan 1.
2. Jumlah total semua peluang sama dengan 1.
Contoh 1: Apakah berikut ini merupakan grafik fungsi massa peluang?

Tidak, grafik tersebut bukan merupakan fungsi massa peluang karena tidak memenuhi kedua syarat yang ada. Pertama, peluang mendapatkan 3 adalah 4 bukan nilai antara 0 sampai 1. Kedua, jumlah semua peluangnya adalah 8 bukan 1.
Selanjutnya, diberikan himpunan kejadian atau bilangan, kita akan mencari cara untuk membentuk sebuah fungsi massa peluang.
Contoh 2: Sebuah tas berisi 6 kelereng hijau, 4 kelereng oranye, 8 kelereng merah, 16 kelereng birum dan 6 kelereng kuning. Bentuklah sebuah distribusi fungsi massa peluang.
Pertama, kita akan menentukan peluang dari setiap hasil dengan membentuk tabel. Untuk menentukan peluang kita perlu mengambil banyaknya kajadian yang dicari dibagi jumlah semua kejadian. Sebagai contoh, untuk kelereng hijau, kita mempunyai 6 kelereng hijau dan jumlah semua kelereng adalah 6+4+8+16+6=40 kelereng. Sehingga peluang kelereng hijau adalah 6/40=.15
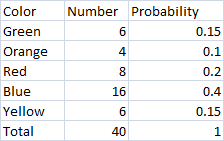
Kita dapat melihat bahwa ternyata ini merupakan fungsi massa peluang karena semua peluang terletak diantara 0 dan 1 dan jumlah semua peluang adalah 1.
Akhirnya, kita dapat menggunakan peluang di atas untuk mencari distribusi.

Membaca peluang dari bagan ini sangat mudah. Sebagai contoh, jika kita mencari pepluang dari kelereng merah atau biru maka kita hanya perlu menghitung 2+.4=.6.