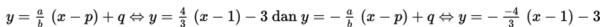Menggambar Kurva Hiperbola

Menggambar Kurva Hiperbola - Dalam topik ini kalian akan belajar tentang menggambar kurva hiperbola. Topik ini sangat berkaitan dengan topik konsep hiperbola. Oke, mari kita mulai topik ini. Tetap fokus!!!

1. Menggambar Kurva Hiperbola

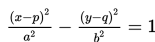
Hiperbola ini berpusat di M(p,q), sumbu utama sejajar dengan sumbu X, panjang sumbu mayor 2a, dan panjang sumbu minor 2b. 
Langkah-langkah dalam menggambar kurva parabola adalah :
a. Menentukan koordinat titik pusat M(p,q).
b. Menentukan persamaan sumbu utama (y = q) dan persamaan sumbu imajiner (x = p).
c. Menentukan koordinat titik puncak yaitu A(p+a,q) dan A’(p-a,q), 
d. Menentukan koordinat titik ujung sumbu minor yaitu B(p,q-b) B dan B’(p,q+b).
e. Menentukan koordinat titik fokus yaitu F1(p-c,q) dan F2(p+c,q).
f. Menentukan nilai eksentrisistas

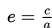
g. Menentukan persamaan direktriks yaitu

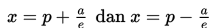
h. Menentukan persamaan asimtot yaitu

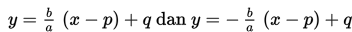
Contoh 1
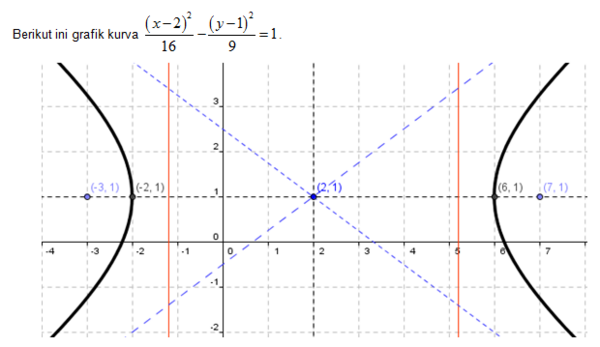
Gambarlah kurva hiperbola

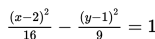
Penyelesaian:
Dari persamaan hiperbola

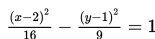
diperoleh nilai p = 2, q = 1, a2 = 16 <=> a = 4, b2 = 9 <=> b = 3. Selanjutnya, kita cari nilai c dengan

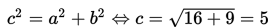
a. Koordinat titik pusat adalah M(p,q) = M(2,1).
b. Persamaan sumbu utama adalah y = 1, persamaan sumbu imajiner adalah x = 2.
c. Koordinat titik puncaknya adalah A(p+a,q) = A(6,1)dan A’(p-a,q) = A’(-2,1).
d. Koordinat titik ujung sumbu minor adalah B(p,q-b) = B(2,-2) dan B’(p,q+b) = B(2,4)
e. Koordinat titik fokus di F1(p-c,q) = F1(-3,1) dan F2(p+c,q) = F2(7,1).
f. Nilai eksentrisistas

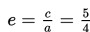
g. Persamaan direktriks adalah

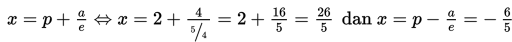
h. Persamaan asimtot adalah

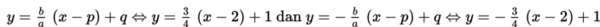
1. Menggambar Kurva Hiperbola

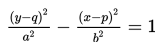
Hiperbola ini berpusat di M(p,q), sumbu utama sejajar dengan sumbu Y, panjang sumbu mayor 2a, dan panjang sumbu minor 2b.
Langkah-langkah dalam menggambar kurva hiperbola :
a. Menentukan koordinat titik pusat M(p,q).
b. Menentukan sumbu utama (x = p) dan sumbu imajiner (y = q).
c. Menentukan Koordinat titik puncak yaitu A(p,q+a) dan A’(p,q-a) 
d. Menentukan koordinat titik ujung sumbu minor yaitu B(p-b,q) dan B’(p+b,q).
e. Menentukan koordinat titik fokus yaitu F1(p,q-c) dan F2(p,q+c) 
f. Menentukan nilai eksentrisistas

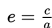
g. Menentukan persamaan direktris yaitu

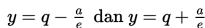
h. Menentukan persamaan asimtot yaitu

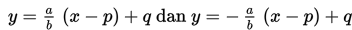
Contoh 2
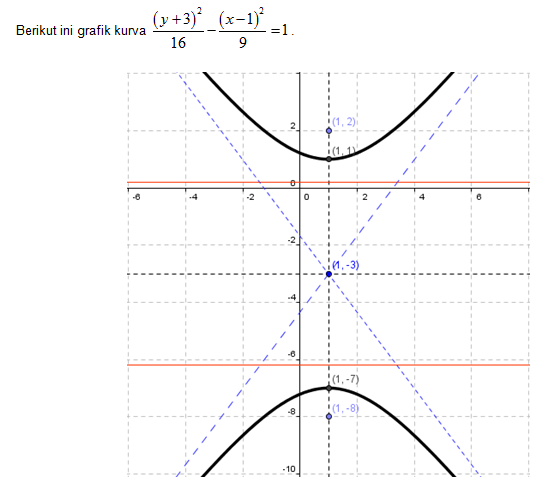
Gambarlah kurva hiperbola

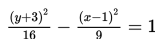
Penyelesaian:
Dari persamaan hiperbola

diperoleh nilai p = 1, q = -3, a2 = 16 <=> a = 4, b2 = 9 <=> b = 3.
Kita cari nilai c dengan

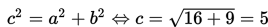
a. Koordinat titik pusat M(p,q) = M(1,-3).
b. Persamaan sumbu utama adalah x = 1, persamaan sumbu imajiner adalah y = -3.
c. Koordinat titik puncak adalah A(p,q+a) = A(1,1) dan A’(p,q-a) = A(1,-7). 
d. Koordinat titik ujung sumbu minor adalah B(p-b,q) = B(-2,-3) dan B’(p+b,q) = B(4,-3).
e. Koordinat titik fokus di F1(p,q-c) = F1(1,-8) dan F2(p,q+c) = F2(1,2) 
f. Nilai eksentrisistas

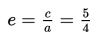
g. Persamaan direktris adalah

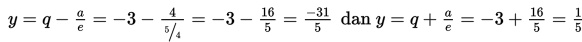
h. Persamaan asimtot adalah