Ketepatan dari perkiraan kita akan meningkat seiring dengan meningkatnya besar ruang sampel dari eksperimen tersebut. Hasil perkiraan akan sama dengan nilai mutlak dari probabilitasnya ketika ukuran ruang sampelnya mendekati tak hingga besarnya .
Probabilitas empiris P(E), dari suatu kejadian E adalah ekspektasi/harapanmunculnya kejadian E terhadap seluruh kejadian pada ruang sampel.
Kumpulan dari probabilitas dari semua hasil eksperimen yang mungkin muncul disebut dengan Distribusi Probabilitas. .
Probabilitas dari sebuah nilai dalam variabel random adalah perbandingan antara frekuensi nilai tersebut terhadap ukuran dari data sampel. Ukuran dari data sampel adalah jumlah dari semua frekuensinya. Jadi, persamaan untuk ekspektasi dari suatu variabel random X untuk kejadian empiris adalah :
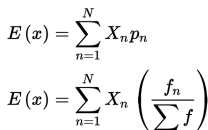
Pada pelajaran ini, kita sebut
N = semua nilai-nilai yang ada pada variable random
fn = frekuensi dari frequency of the value of random variable xn
CONTOH 1:
Kita lakukan sebuah survey acak untuk mencari tahu jumlah anak-anak di sebuah Kota. Hasilnya adalah sebagai berikut ::
Jumlah Anak | Jumlah Rumah
0 : 11
1 : 25
2 : 47
3 : 50
4 : 17
Bagaimanakah distribusi probabilitas dari anak-anak? Juga, , Berapa banyak anak yang diharapkan dalam 1000 rumah (diambil sampel random, dibulatkan ke bilangan bulat terdekat)?.
PENYELESAIAN:
Dari soal, dapat diketahui jumlah orang yang disurvey adalah :
jumlah orang yang disurvey = 11+25+47+50+17 = 150
Oleh karena itu distribusi probabilitas:
11/150, 25/150, 47/150, 50/150, 17/150
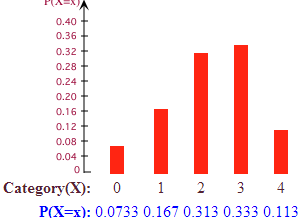
Lalu, dengan mengalikan ‘x’ dengan F(x)
0, 25/150, 94/150, 150/150, 68/150
Dengan menjumlah jumlah-jumlah diatas, kita peroleh:
337/150
dengan mengalikan dengan 1000:
2247
Jadi, nilai ekspektasi dari banyakanya anak dalam 1000 rumah yang dipilih secara acak adalah 2247.
CONTOH 2:
Sebuah permainan melempar dart , yang menembak pada titik-titik acak
dalam sebuah persegi panjang. Jika dart menembus pada lingkaran merah, pemain menang $10 , jika dart menembus lingkaran biru, pemain menang $14 dan pemain menang $20 jika dart menembus segitiga hitam manapun. pemain harus membayar $10 untuk ikut bermain dart, berapakah ekspektasi pemain untuk memperoleh/kehilangan uang?

PENYELESAIAN:
Misalkan X adalah nilai uang yang diperoleh pemain:
Nilai dari X | Probabilitas | Produk
10 Π/16 1.96
14 Π/16 2.75
20 1/4 5
Total 9.71
Jadi, pemain akan berharap kehilangan 29 sen dalam setiap permainan.