Kumpulan dari peluang semua kejadian yang mungkin terjadi adalah distribusi probabilitas.
Menentukan Probabilitas Empiris
Probabilitas empiris dihitung secara analitis, yaitu dengan menggunakan pengetahuan kita tentang sifat percobaan daripada melalui eksperimen langsung
Contoh 1:
Sebuah koin yang seimbang dilemparkan. Karena sisi gambar dan sisi angka seimbang, kita simpulkan
bahwa distribusi probabilitas empirisnya adalah
P(H) = 1/2 , P(T) = 1/2.
Contoh 2:
Melemparkan sebuah dadu yang seimbang. Karena semua hasil yang mungkin dari sebuah dadu adalah seimbang, kita peroleh
P(1) = 1/6
P(1) = 1/6
Begitu juga, P(2) = 1/6, P(3) = 1/6, . . . , P(6) = 1/6.
Contoh 3:
Melemparkan sepasang dadu yang seimbang. Terdapat sebanyak 6 x 6 kemungkinan yang bisa terjadi.
Peluang dari kejadian yang muncul tidak bisa kurang dari 1/36 .
Ada 11 variasi jumlah angka dadu:
{ (1,1), (1,2), (1,3), (1,4), (1,5), (1,6),
(2,1), (2,2), (2,3), (2,4), (2,5), (2,6),
(3,1), (3,2), (3,3), (3,4), (3,5), (3,6),
(4,1), (4,2), (4,3), (4,4), (4,5), (4,6),
(5,1), (5,2), (5,3), (5,4), (5,5), (5,6),
(6,1), (6,2), (6,3), (6,4), (6,5), (6,6) }
If E is the event that the sum of numbers is 4, then E = {(1, 3), (2, 2),
(3, 1)}. Since all 36 outcomes are equally likely, we have
P(E) = 3/36 = 1/12 = 0.8333
Distribusi probabilitas untuk kasus ini ditunjukkan oleh gambar di bawah ini.
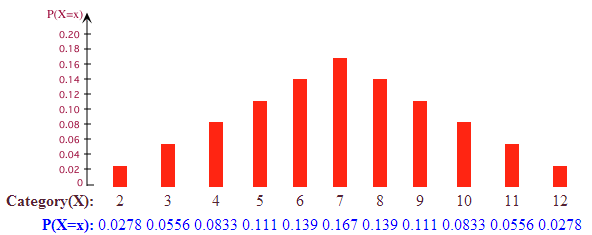
Contoh 4:
Berapakah probabilitas munculnya dua sisi gambar dan satu sisi angka pada saat tiga buah koin yang seimbang dilempar bersama-sama?
PENYELESAIAN:
Misalkan X adalah jumlah munculnya sisi gambar pada setiap pelemparan tiga buah koin.
Banyaknya kejadian yang mungkin terjadi = 23 .Ruang sampelnya adalah
{(H,H,H),(H,H,T),(H,T,H),(T,H,H),(T,T,H),(T,H,T),(H,T,T),(T,T,T)}
Jadi,
P(X = 2) = 3/8 = 0.375
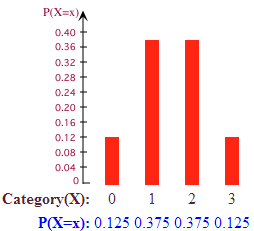
Contoh 5:
Sebuah survey acak dilakukan untuk mencari jumlah anak di sebuah kota Hasilnya adalah sebagai berikut:
Jumlah anak | Jumlah rumah
0 : 11
1 : 25
2 : 47
3 : 50
4 : 17
Berapa distribusi probabilitas dari anak-anak tersebut? Selain itu, berapa anak yang diharapkan dapat ditemukan di 1000 rumah yang dipilih secara acak? (Bulatkan hingga ke bilangan bulat terdekat)
PENYELESAIAN:
Jumlah total responden survey adalah:
Jumlah total responden survey = 11+25+47+50+17 = 150
Dengan demikian, distribusi probabilitas 'F(x)' adalah:
11/150, 25/150, 47/150, 50/150, 17/150
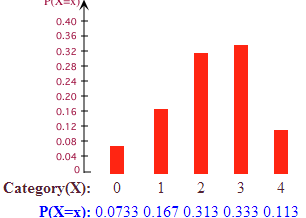
Sekarang, kalikan 'x' dengan F(x)
0, 25/150, 94/150, 150/150, 68/150
Jumlahkan nilai-nilai di atas:
337/150
Kalikan dengan 1000:
2247
Jadi, nilai harapan jumlah anak yang ditemukan di 1000 rumah yang dipilih secara acak adalah 2247.