Untuk menghitung peluang terjadinya suatu kejadian, kita membagi jumlah cara kejadian itu dapat terjadi dengan jumlah semua kemungkinan hasil yang ada.
Dalam istilah teknis, nilai harapan, E(X), sama dengan:
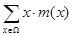
di mana x adalah jumlah kejadian di dalam ruang sampel Ω (yaitu semua kejadian yang mungkin terjadi), dan m(x) adalah fungsi distribusi (yaitu peluang suatu kejadian muncul).
Contoh 1
Misalkan kita melemparkan koin sebanyak tiga kali. Andaikan X sama dengan jumlah munculnya sisi gambar. Hitunglah nilai harapan dari X.
Ingat, nilai harapan dari kejadian tak tentu adalah jumlah dari semua kemungkinan yang ada dikalikan masing-masing peluang kejadian tersebut. Kejadian yang mungkin dari X adalah 0, 1, 2, dan 3. Dengan kata lain, lemparan tersebut dapat memunculkan 0 sisi gambar, 1 sisi gambar, 2 sisi gambar, atau semua 3 sisi gambar.
Peluang munculnya 0 sisi gambar adalah 1/8 .
Peluang munculnya 1 sisi gambar adalah 3/8.
Peluang munculnya 2 sisi gambar adalah 3/8.
Peluang munculnya 3 sisi gambar adalah 1/8.
(Untuk memperoleh peluang-peluang ini, kita dapat membuat daftar semua kejadian yang mungkin dari pelemparan sebuah koin sebanyak 3 kali/ ada 8 kemungkinan.)
Jadi, nilai harapan dari X sama dengan 0(1/8)+1(3/8)+2(3/8)+3(1/8) = 3/2.
Contoh 2
Ben ingin bermain judi, jadi dia menawari kita permainan seperti ini: Untuk bermain, kita harus melemparkan sebuah dadu dan membayar $2 setiap lemparan. Jika dari lemparan itu muncul angka 1, Ben akan membayar kita $5. Jika muncul angka genap (2, 4, atau 6), dia akan memberi kita $3. Jika tidak, kita tidak mendapatkan apa-apa. Haruskan kita memainkan permainan ini dengannya?
Kita akan mengalikan pembayaran yang diperoleh ($) dari masing-masing kemunculan angka dengan peluang masing-masing kejadian yang mungkin terjadi. Jumlah dari hasil perkaliannya adalah nilai harapan.
Ada enam kejadian yang mungkin, yaitu munculnya angka 1, 2, 3, 4, 5, dan 6. Peluang masing-masing kejadian adalah 1/6 . Pembayaran yang diperoleh adalah $5 untuk angka 1, $3 untuk angka 2, 4, atau 6, dan $0 untuk angka 3 atau 5.
Dengan demikian, nilai harapannya adalah: 5(1/6)+3(1/6)+ 3(1/6)+3(1/6)+0(1/6)+0(1/6)= 14/6 = 2.33… , jadi secara umum kita mempunyai harapan untuk menang $2.50 pada setiap kali lemparan. Jika kita hanya membayar $2 untuk setiap kali melempar, maka kesempatan untuk mendapatkan untung lebih besar. Jadi kalau kita senang berjudi, kita harus ikut bermain.
Contoh 3
Bill-Fold Company membutuhkan $5 untuk membuat sebuah dompet kanvas dan $12 untuk membuat sebuah dompet kulit. Dompet kanvas dijual $9 dan dompet kulit dijual $20. Perusahaan itu telah memperhitungkan bahwa sekitar 40% dari dompet yang terjual adalah dompet kanvas, dan 60% -nya dompet kulit. Berapakah keuntungan yang bisa mereka harapkan dari setiap dompet?
Pertama, hitunglah keuntungan penjualan dari setiap dompet. Keuntungan dari penjualan sebuah dompet kanvas adalah $4 sedangkan keuntungan dari penjualan sebuah dompet kulit adalah $8. Prosentase setiap jenis dompet yang terjual dapat dipandang sebagai peluang – peluang seseorang akan memberi dompet kanvas adalah 40%, atau 0.4, dan peluang seseorang akan membeli dompet kulit adalah 60%, atau 0.6. Keuntungan yang diharapkan adalah 0.4(4) + 0.6(8) = 6.4 , jadi keuntungan yang diharapkan dari setiap dompet adalah $6.40.