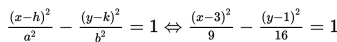Irisan kerucut adalah tempat kedudukan titik-titik pada bidang. Perbandingan jarak dari titik itu ke titik tertentu dengan jarak dari titik itu ke garis tertentu selalu tetap. Harga tetap ini disebut eksentrisitas (ditulis e), titik tertentu disebut fokus dan garis tertentu disebut direktris.
a. Jika e = 1, maka irisan kerucut itu berbentuk parabola
b. Jika 0 < e < 1, maka irisan kerucut itu berbentuk ellips
c. Jika e = 0, maka irisan kerucut itu berbentuk lingkaran
d. Jika e > 1, maka irisan kerucut itu berbentuk hiperbola
a. Jika e = 1, maka irisan kerucut itu berbentuk parabola
b. Jika 0 < e < 1, maka irisan kerucut itu berbentuk ellips
c. Jika e = 0, maka irisan kerucut itu berbentuk lingkaran
d. Jika e > 1, maka irisan kerucut itu berbentuk hiperbola
PARABOLA
Tentunya kalian masih ingat materi tentang parabola. Apabila kalian lupa perhatikanlah keterangan berikut ini. Parabola adalah tempat kedudukan titik-titik, sedemikian sehingga jarak dari titik itu ke titik fokusnya sama dengan jarak dari titik itu ke garis direktrisnya. Agar kalian lebih mudah dalam mempelajari materi selanjutnya, kalian dapat menggunakan ringkasan materi dalam tabel berikut ini.


ELLIPS
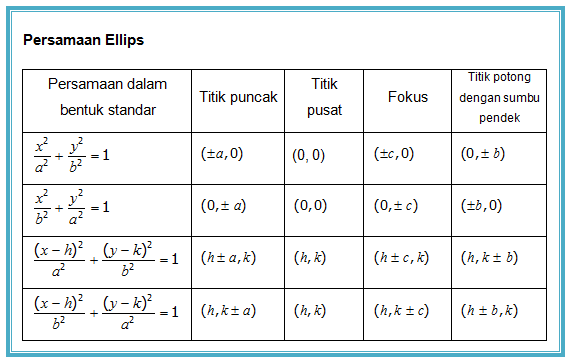
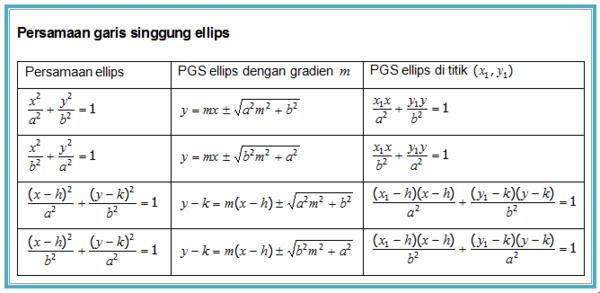
Masih ingatkah kalian materi tentang ellips? Mari kita perhatikanlah keterangan berikut ini. Ellips adalah tempat kedudukan titik-titik, sedemikian rupa sehingga perbandingan jarak dari titik itu ke titik fokusnya dan terhadap garis direktrisnya adalah tetap dan besarnya sama dengan e dengan 0 < e < 1. Ringkasan materi dalam tabel berikut ini dapat digunakan untuk mempermudah kalian dalam mempelajari materi selanjutnya.
HIPERBOLA
Mari kita ingat kembali tentang pengertian hiperbola. Hiperbola adalah tempat kedudukan titik-titik sedemikian rupa sehingga perbandingan jarak dan titik itu ke titik fokusnya dan jarak dari titik itu ke garis direktrisnya selalu tetap yaitu e dengan e > 1.
Ringkasan dalam tabel berikut ini dapat digunakan untuk mempelajari materi selanjutnya.
Ringkasan dalam tabel berikut ini dapat digunakan untuk mempelajari materi selanjutnya.

Mari kita mencermati beberapa contoh berikut ini.
Contoh 1:
Tentukan sumbu simetri, titik puncak, fokus dan direktris dari parabola yang persamaannya seperti berikut :
1. y2 = 8x
2. x2 = -4y
1. y2 = 8x
2. x2 = -4y
Penyelesaian
y2 = 8x merupakan parabola dengan persamaan y2 = 4cx.
Dengan demikian, sumbu simetrinya y =0 dan titik puncaknya di (0,0).
Selanjutnya, karena 4c = 8 ⟺ c = 2 maka fokusnya (2,0) dan direktriksnya adalah x = -2.
Dengan demikian, sumbu simetrinya y =0 dan titik puncaknya di (0,0).
Selanjutnya, karena 4c = 8 ⟺ c = 2 maka fokusnya (2,0) dan direktriksnya adalah x = -2.
x2 = -4y merupakan parabola dengan persamaan x2 = 4cy.
Dengan demikian, sumbu simetrinya x = 0 dan titik puncaknya di (0,0).
Selanjutnya, karena 4c = -4 ⟺ c = -1 maka fokusnya (0,-1) dan direktriksnya adalah y = -1.
Dengan demikian, sumbu simetrinya x = 0 dan titik puncaknya di (0,0).
Selanjutnya, karena 4c = -4 ⟺ c = -1 maka fokusnya (0,-1) dan direktriksnya adalah y = -1.
Contoh 2:
Tentukan persamaan parabola jika diketahui:
1. Fokus (3,5) dan titik puncak (3,9)
2. Titik puncak (3,5) dan direktris x = -1
1. Fokus (3,5) dan titik puncak (3,9)
2. Titik puncak (3,5) dan direktris x = -1
Penyelesaian
Fokus (3,5) dan titik puncak (3,9)
Dari koordinat titik fokus dan koordinat titik puncak yang diketahui, kita dapat mengetahui bahwa persamaan parabola yang ingin dicari adalah persamaan parabola dengan titik fokus (h , k+c) dan titik puncak (h,k).
Berdasarkan soal, maka h = 3 dan k = 9.
Akibatnya, k + c = 5 ⟺ 9 + c = 5 ⟺ c = -4.
Akibatnya, k + c = 5 ⟺ 9 + c = 5 ⟺ c = -4.
Dengan demikian, persamaan parabolanya adalah :
(x - h)2 = 4c(y - k) ⟺ (x - 3)2 = 4(-4)(y - 9) ⟺ (x - 3)2 = -16(y - 9)
(x - h)2 = 4c(y - k) ⟺ (x - 3)2 = 4(-4)(y - 9) ⟺ (x - 3)2 = -16(y - 9)
Puncak (3,5) dan direktriks x = -1
Dari koordinat titik puncak dan direktris yang diketahui, kita dapat mengetahui bahwa persamaan parabola yang ingin dicari adalah persamaan parabola dengan titik puncak (h,k) dan direktris x = h -c.
Berdasarkan soal, maka h = 3 dan k = 5.
Akibatnya, x = h - c ⟺ -1 = 3 - c ⟺ c = 4.
Akibatnya, x = h - c ⟺ -1 = 3 - c ⟺ c = 4.
Dengan demikian, persamaan parabolanya adalah :
(y - k)2 = 4c(x - h) ⟺ (y - 5)2 = 4(4)(x - 3) ⟺ (y - 5)2 = 16(x - 3)
(y - k)2 = 4c(x - h) ⟺ (y - 5)2 = 4(4)(x - 3) ⟺ (y - 5)2 = 16(x - 3)
Contoh 3:
Tentukan persamaan garis singgung ellips 4x2 + y2 = 4 dengan gradien 2.
Penyelesaian
Bentuk baku persamaan ellips 4x2 + y2 = 4 adalah x2/1 + y2/4 = 1.
Dengan demikian,
• a2 = 4 ⟺ a = 2, a > 0
• b2 = 1 ⟺ b = 1, b > 0
• a2 = 4 ⟺ a = 2, a > 0
• b2 = 1 ⟺ b = 1, b > 0
Selanjutnya, karena sumbu panjang ellips berimpit dengan sumbu Y , maka persamaan garis singgung ellips dengan gradien 2 adalah :
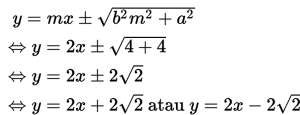
Contoh 4:
Tentukan persamaan hiperbola, jika diketahui:
1. Pusat (2,5), puncak (2,7), dan fokus (2,0)
2. Puncak (6,1) dan (0,1) ; fokus (8,1)
1. Pusat (2,5), puncak (2,7), dan fokus (2,0)
2. Puncak (6,1) dan (0,1) ; fokus (8,1)
Penyelesaian
(1)
Dari koordinat titik pusat, titik puncak, dan titik fokus yang diketahui, kita dapat mengetahui bahwa persamaan hiperbola yang ingin dicari adalah persamaan hiperbola dengan titik pusat (h,k), titik puncak (h, k ± a), dan titik fokus (h, k ± c).
Dari koordinat titik pusat, titik puncak, dan titik fokus yang diketahui, kita dapat mengetahui bahwa persamaan hiperbola yang ingin dicari adalah persamaan hiperbola dengan titik pusat (h,k), titik puncak (h, k ± a), dan titik fokus (h, k ± c).
Dengan demikian,
• Pusat (2,5) ⇒ (2,5) = (h,k) ⇒ h = 2 dan k = 5
• Puncak (2,7) ⇒ k ± a = 7 ⇒ 5 ± a = 7 ⇒ a = 2
• Fokus (2,1) ⇒ k ± c = 0 ⇒ 5 ± c = 0 ⇒ c = 5
• Pusat (2,5) ⇒ (2,5) = (h,k) ⇒ h = 2 dan k = 5
• Puncak (2,7) ⇒ k ± a = 7 ⇒ 5 ± a = 7 ⇒ a = 2
• Fokus (2,1) ⇒ k ± c = 0 ⇒ 5 ± c = 0 ⇒ c = 5
Akibatnya, b2 = c2 - a2 = 25 - 4 = 21.
Jadi, persamaan parabola yang dimaksud adalah :
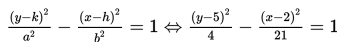
(2)
Dari koordinat titik puncak (6,1) dan (0,1) dan titik fokus (8,1), kita dapat mengetahui bahwa persamaan parabola yang ingin dicari adalah persamaan parabola dengan titik pusat (h,k), titik puncak (h ± a, k), dan titik fokus (h ± c, k).
Dengan demikian,
- Puncak (6,1) dan (0,1) ⇒ (h ± a, k) = (3 ± 3, 1) ⇒ h = 3, a = 3, k = 1
- Fokus (8,1) ⇒ h ± c = 8 ⇒ 3 ± c = 8 ⇒ c = 5
Akibatnya, b2 = c2 - a2 = 25 - 9 = 16.
Jadi, persamaan parabola yang dimaksud adalah :