Refleksi terhadap Sumbu Y

Refleksi terhadap Sumbu Y -  Pada topik sebelumnya kalian telah belajar tentang refleksi terhadap sumbu horizontal (sumbu X). Setelah mempelajari materi tersebut, tentunya kalian telah mengetahui bahwa ciri suatu refleksi adalah jarak setiap titik pada bangun semula ke cermin sama dengan jarak setiap titik pada bangun bayangan ke cermin. Selain itu, sudut yang dibentuk oleh sumbu X dengan garis yang menghubungkan setiap titik ke bayangannya berupa sudut siku-siku.

Nah, dalam topik kali ini kalian akan belajar tentang refleksi terhadap sumbu vertikal (sumbu Y).

Mari kita temukan perbedaan antara hasil refleksi suatu titik atau kurva terhadap sumbu Y dan sumbu X dalam uraian konsep dasar berikut.

Konsep Dasar

Refleksi atau pencerminan terhadap sumbu Y dari suatu bangun geometri memetakan setiap titik pada bangun geometri tersebut terhadap sumbu Y sebagai sumbu cermin atau sumbu simetri.

Mari kita perhatikan gambar berikut:

Berdasarkan gambar di atas, tampak bahwa jarak setiap titik pada segitiga ABC ke sumbu Y sama dengan jarak setiap titik bayangannya ke sumbu Y (AP= A’P, BQ= B’Q, dan CR = C’R). Tampak pula bahwa sudut yang dibentuk oleh sumbu Y dengan garis yang menghubungkan setiap titik ke bayangannya berupa sudut siku-siku.

Selanjutnya mari perhatikan gambar berikut:

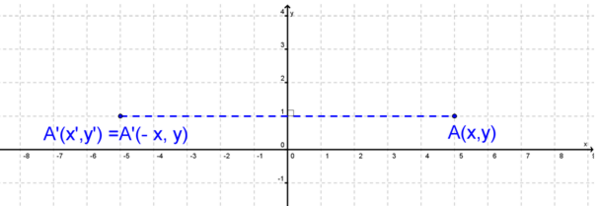
Dalam gambar di atas, dapat kita tarik kesimpulan bahwa hasil refleksi titik A(x, y)terhadap sumbu Y adalah titik A'(x, y), dimana x’ = -x dan y’ = y.

Selanjutnya, karena x' = -x = (-1)x + (0)y dan y' = y = (0)x + (1)y, maka hasil refleksi titikA(x, y) terhadap sumbu Y dapat dinyatakan dalam bentuk persamaan matriks sebagai berikut: (x′y′ )=(−1001 )(xy ) $\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)$.

Nah, agar kalian lebih mudah memahami konsep refleksi terhadap sumbu Y, mari kita cermati beberapa contoh soal berikut.

Contoh 1

Tentukan bayangan titik A(5, 12) oleh refleksi terhadap sumbu Y.

Penyelesaian:

Kalian dapat menyelesaikan soal ini menggunakan dua cara.

Cara 1

Oleh karena hasil refleksi titik A(x, y) terhadap sumbu Y adalah titik A'(-x, y), maka titikA(5, 12) akan dipetakan ke titik A'(-5, 12). Dengan demikian, bayangan titik A(5, 12) oleh refleksi terhadap sumbu Y adalah A'(-5, 12).

Cara 2

Berdasarkan matriks transformasi refleksi terhadap sumbu Y, diperoleh hubungan sebagai berikut:

(x′y′ )====(−1001 )(xy )(−1001 )(512 )((−1)(5)+(0)(12)(0)(5)+(1)(12) )(−512 ) $\begin{array}{lll}\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)& =& \left(\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)\\ & =& \left(\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right)\left(\begin{array}{c}5\\ 12\end{array}\right)\\ & =& \left(\begin{array}{c}(-1)(5)+(0)(12)\\ (0)(5)+(1)(12)\end{array}\right)\\ & =& \left(\begin{array}{c}-5\\ 12\end{array}\right)\end{array}$

Dengan demikian, bayangan titik A(5, 12) oleh refleksi terhadap sumbu Y adalah A'(-5, 12).

Nah, berdasarkan kedua cara di atas, manakah yang lebih mudah?

Contoh 2

Diberikan persegi ABCD dengan koordinat keempat titik sudutnya adalah sebagai berikut: A(-5, 1), B(-1, 1), C(-1, 5), dan D(-5, 5). Tentukan bayangan persegi ABCD oleh refleksi terhadap sumbu Y.

Penyelesaian:

Oleh karena hasil refleksi titik (x, y) terhadap sumbu Y adalah (-x, y), maka bayangan titik A(-5, 1), B(-1, 1), C(-1, 5), dan D(-5, 5) oleh refleksi terhadap sumbu Y berturut-turut adalah A'(5, 1), B'(1, 1), C'(1, 5), dan D'(5, 5).

Pada contoh 1 dan 2, kalian telah belajar tentang bagaimana cara menentukan hasil refleksi suatu titik terhadap sumbu Y. Nah, pada contoh 3 dan 4 kalian akan belajar tentang cara menentukan hasil refleksi suatu garis dan kurva terhadap sumbu Y.

Contoh 3

Tentukan bayangan garis 8x + 11y = 9 bila direfleksikan terhadap sumbu Y.

Penyelesaian:

Berdasarkan matriks transformasi refleksi terhadap sumbu Y, diperoleh hubungan sebagai berikut:

(x′y′ )=(−1001 )(xy )=(−xy )$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)=\left(\begin{array}{c}-x\\ y\end{array}\right)$

Jika kita substitusikan x = -x' dan y = y' ke dalam persamaan garis 8x + 11y = 9, maka diperoleh hasil sebagai berikut:

8x+11y=9⇔8(−x′)+11y′=9⇔−8x′+11y′=9 $\begin{array}{rl}& 8x+11y=9\\ & \iff 8(-x^{\prime })+11y^{\prime }=9\\ & \iff -8x^{\prime }+11y^{\prime }=9\end{array}$

Dengan demikian, bayangan garis 8x + 11y = 9 bila direfleksikan terhadap sumbu Yadalah -8x + 11y = 9.

Contoh 4

Diberikan persamaan parabola y = x2 + 4x + 3. Tentukan bayangan parabola ini apabila direfleksikan terhadap sumbu Y.

Penyelesaian:

Berdasarkan matriks transformasi refleksi terhadap sumbu Y, diperoleh hubungan sebagai berikut:

(x′y′ )=(−1001 )(xy )=(−xy )$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)=\left(\begin{array}{c}-x\\ y\end{array}\right)$

Jika kita substitusikan x = -x' dan y = y' ke dalam persamaan parabola y = x2 + 4x + 3, maka diperoleh hasil sebagai berikut:

y=x2+4x+3$y=x^2+4x+3$
⇔y′=(−x′)2+4(−x′)+3$\iff y^{\prime }={(-x^{\prime })}^2+4(-x^{\prime })+3$
⇔y′=(x′)2−4x′+3$\iff y^{\prime }={\left(x^{\prime }\right)}^2-4x^{\prime }+3$

Dengan demikian, bayangan parabola y = x2 + 4x + 3 bila direfleksikan terhadap sumbuY adalah y = x2 - 4x + 3.

Kadang kala, persamaan suatu kurva tidak diketahui, namun hasil refleksi kurva terhadap sumbu Y diketahui.

Nah, tahukah kalian bagaimana cara menentukan persamaan kurva semula?

Mari kita temukan jawabannya dalam contoh soal berikut.

Contoh 5

Persamaan suatu kurva oleh pencerminan terhadap sumbu Y adalah x2 + y2 + 2x - 4y - 9 = 0. Tentukan persamaan kurva semula.

Penyelesaian:

Oleh karena persamaan suatu kurva oleh pencerminan terhadap sumbu Y adalah x2 +y2 + 2x - 4y - 9 = 0, maka persamaan tersebut dapat dinyatakan dalam bentuk (x')2 + (y')2+ 2x' - 4y' - 9 = 0.

Berdasarkan matriks transformasi refleksi terhadap sumbu Y, diperoleh hubungan sebagai berikut:

(x′y′ )=(−1001 )(xy )=(−xy )$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)=\left(\begin{array}{c}-x\\ y\end{array}\right)$

Jika kita substitusikan x' = -x dan y' = y ke dalam persamaan (x')2 + (y')2 + 2x' - 4y' - 9 = 0, maka diperoleh hasil sebagai berikut:

(x′)2+(y′)2+2x′−4y′−9=0${\left(x^{\prime }\right)}^2+{\left(y^{\prime }\right)}^2+2x^{\prime }-4y^{\prime }-9=0$
⇔(−x)2+y2+2(−x)−4y−9=0$\iff {(-x)}^2+y^2+2(-x)-4y-9=0$
⇔x2+y2−2x−4y−9=0$\iff x^2+y^2-2x-4y-9=0$

Dengan demikian, persamaan kurva semula adalah x2 + y2 - 2x - 4y - 9 = 0.

Apakah kalian sudah paham dengan materi dalam topik ini?

Ayo kerjakan latihan soal dalam topik ini untuk menguji pemahaman kalian.