Penerapan Integral Tentu dalam Kehidupan Sehari-Hari

Penerapan Integral Tentu dalam Kehidupan Sehari-Hari - Pernahkah kamu memperhatikan sebuah roller coaster di taman hiburan? Jika kita mengetahui persamaan kelajuan dari roller coaster tersebut, maka dengan memanfaatkan integral tentu, kita dapat menghitung panjang rute yang telah ditempuh oleh roller coaster tersebut. 

Caranya dengan mengintegralkan fungsi kelajuan roller coaster dengan batas pengintegralan dari waktu pengamatan mula-mula hingga waktu yang diinginkan. Dengan demikian, dapat kita peroleh panjang rute yang ditempuh dalam selang waktu tersebut.

        

Permasalahan yang berkaitan dengan fungsi kecepatan seperti ini merupakan salah satu penerapan integral tentu dalam kehidupan sehari-hari. Pada materi ini, akan dibahas juga penerapan integral tentu dalam permasalahan sehari-hari lainnya. Untuk itu, perhatikanlah materi ini dengan saksama.

Penerapan integral tentu yang pertama akan kita bahas adalah mengenai penentuan luas daerah di bawah kurva. Akan tetapi sebelumnya, mari kita ingat kembali cara menentukan luas daerah yang dibatasi oleh kurva positif.

Misalkan A adalah daerah yang dibatasi kurva y = f(x), x = a, x = b dan sumbu-x, denganf(x) ≥ 0 untuk a ≤ x ≤ b, seperti pada gambar berikut.

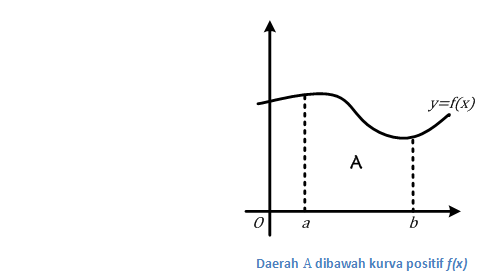
Luas daerah A tersebut, yang kita lambangkan dengan L(A) dapat dihitung dengan,

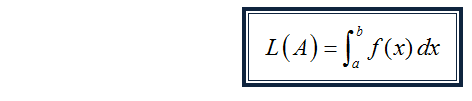
Agar lebih memahami kembali cara menentukan luas daerah di bawah kurva dengan menggunakan integral tentu, perhatikanlah contoh berikut ini.

☀ Contoh Soal 1 ☀

Sebidang tanah dibatasi oleh daerah yang berbentuk seperti pada gambar di bawah ini.

Jika seorang matematikawan merumuskan persamaan parabola pada sisi lengkung dari tanah tersebut dengan f(x)=−x2+2x+2$f(x)=-x^2+2x+2$, dengan x dalam meter dan panjang sisi di depan parabola adalah 2 m, maka luas tanah tersebut adalah….

☀ Penyelesaian: ☀

Berdasarkan informasi yang diketahui pada soal, kita dapat menggambarkan daerah tanah tersebut pada bidang koordinat, seperti pada gambar di bawah ini.

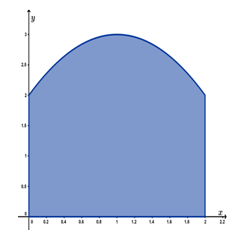
Berdasarkan gambar, terlihat bahwa kurva selalu positif dari x=0$x=0$ hingga x=2$x=2$. Dengan demikian luas daerah tersebut dapat ditentukan dengan sebuah pengintegralan sebagai berikut.

∫20f(x)dx=∫20−x2+2x+2dx=[−13x3+x2+2x]20=−1323+22+2⋅2−(−1303+02+2⋅0)=8−83=163$\begin{array}{l}{<br>}_{}^{}\end{array}$

$\begin{array}{ll}{\int }_0^{2}f(x)dx& ={\int }_0^2-x^2+2x+2dx\\ & ={\left[-\frac{1}{3}{x}^3+x^2+2x\right]}_0^2\\ & =-\frac{1}{3}{2}^3+2^2+2\cdot 2-(-\frac{1}{3}{0}^3+0^2+2\cdot 0)\\ & =8-\frac{8}{3}\\ & =\frac{16}{3}\end{array}$

Jadi, luas tanah tersebut adalah 163$\frac{16}{3}$ m2${\mathrm{m}}^2$.

Penerapan selanjutnya dari integral tentu yaitu menentukan jumlah perubahan pada suatu objek yang diketahui fungsi laju perubahannya. Contohnya, laju perubahan posisi yang kenal sebagai kecepatan dan biaya marginal sebagai perubahan harga akibat penambahan produksi. Jika diketahui fungsi laju perubahan tersebut maka kita dapat menentukan jumlah perubahan yang terjadi pada selang waktu yang diinginkan dengan mengintegralkan fungsi perubahan tersebut dengan batas pengintegralan sesuai dengan selang waktu yang diinginkan.

Misalkan laju perubahan objek diketahui sebagai fungsi f(t), maka jumlah dari perubahan objek dalam interval waktu t=a$t=a$ hingga t=b$t=b$ atau untuk selang a≤t≤b$a\le t\le b$yaitu:

∫baf(t)dt${\int }_a^{b}f(t)dt$

Berikut ini adalah beberapa kasus terkait dengan laju perubahan.

Kecepatan, perpindahan dan panjang lintasan 
Misalkan v(t) adalah fungsi kecepatan objek, maka:

• perpindahan objek dari posisi saat t=a$t=a$ dan posisi saat t=b$t=b$, (selang a≤t≤b$a\le t\le b$) yaitu ∫bav(t)dt${\int }_a^{b}v(t)dt$; dan
• panjang lintasan yang telah ditempuh objek pada interval a≤t≤b$a\le t\le b$ yaitu ∫ba|v(t)|dt${\int }_a^b|v(t)|dt$.

Laju perubahan volume dan perubahan volume
Misalkan V′(t)$V^{\prime }(t)$ adalah fungsi laju perubahan volume, maka total perubahan volume pada interval waktu a≤t≤b$a\le t\le b$ yaitu ∫baV′(t)dt${\int }_a^b{V}^{\prime }(t)dt$.

Laju perubahan biaya produksi dan biaya marginal (C'(x)): 
Misalkan C' (x) adalah biaya marginal dari produksi x unit suatu produk maka perubahan biaya produksi jika banyak barang yang diproduksi diubah dari a menjadi bunit yaitu ∫baC′(x)dx${\int }_a^b{C}^{\prime }(x)dx$.

Sebenarnya masih banyak kasus laju perubahan lain karena kehidupan tidak pernah terlepas dari laju dan perubahan. Namun demikian, kasus di atas adalah kasus-kasus yang dianggap umum. Untuk lebih memahami penerapan ini perhatikan contoh berikut.

☀ Contoh Soal 2 ☀

Sebuah kereta wisata bergerak dengan kecepatan 6t−t2$6t-t^2$. Perpindahan objek dari posisi awal ke posisi saat t=8$t=8$ adalah ….

☀ Penyelesaian: ☀

Jika kita asumsikan posisi awal objek adalah pada saat t = 0, maka perpindahan objek dari posisi awal ke posisi saat t = 8, dapat ditentukan dengan menghitung integral dari fungsi kecepatan 6t−t2$6t-t^2$ dengan rentang 0≤t≤8$0\le t\le 8$.

∫80v(t)dt=∫80(6t−t2)dt=3t2−13t3∣80=3.82−13.83−(3.02−13.03)=643=2113$\begin{array}{rl}{\int }_0^{8}v(t)dt& ={\int }_0^8(6t-t^2)dt\\ & =3t^2-\end{array}$

$\begin{array}{r}\frac{1}{3}{t}^3{\mid }_0^8\\ & ={3.8}^2-\frac{1}{3}{.8}^3-({3.0}^2-\frac{1}{3}{.0}^3)\\ & =\frac{64}{3}\\ & =21\frac{1}{3}\end{array}$

Jadi perpindahan objek dari posisi mula-mula adalah 2113$21\frac{1}{3}$.

Nah, sekarang kamu tentu telah memahami tentang penerapan integral dalam permasalahan sehari-hari bukan? Selanjutnya, kerjakanlah latihan soal berikut, agar kemampuanmu semakin terlatih.