
Untuk menghitung luas danau tersebut, kita dapat membagi (mempartisi) permukaan danau menjadi bangun datar seperti persegi, persegipanjang, segitiga, dan lain-lain. Selain itu, kita juga dapat menghitung luas danau tersebut dengan konsep yang akan kita pelajari berikut ini. Kita dapat mengkombinasikan fungsi-fungsi yang dapat diperoleh pada pinggiran danau sebagai suatu pembatas daerah, kemudian menghitung luas daerah tersebut dengan konsep integral luas. Bagaimana caranya? Mari kita pelajari bersama-sama.
🏠 KONSEP
▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩
Pada topik kali ini, konsep luas daerah yang akan kita pelajari adalah luas daerah yang dibatasi oleh dua fungsi/ kurva. Posisi dua kurva ini menentukan rumus integral yang akan digunakan. Untuk lebih jelasnya, perhatikan uraian berikut ini ya.
☀ Luas daerah antara dua kurva tanpa melalui titik potong
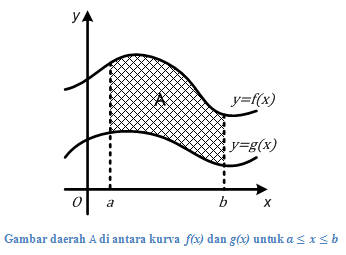
Misalkan A adalah daerah yang dibatasi kurva , , , dan dengan , untuk . Luas daerah A yang dilambangkan dengan L(A) dapat kita hitung dengan integral berikut.
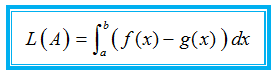
☀ Luas daerah antara dua kurva yang berpotongan di kedua ujungnya
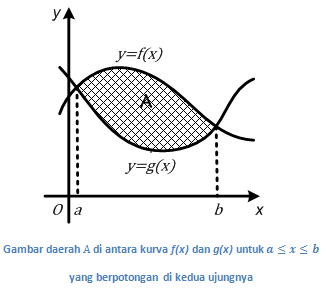
Penentuan luas daerah A pada gambar di atas juga dapat dilakukan dengan menggunakan rumus yang kita peroleh sebelumnya. Misalkan A adalah daerah yang dibatasi kurva dengan dan yang berpotongan di dan dengan , untuk . Luas daerah A yang dilambangkan dengan L(A) dapat kita hitung dengan integral berikut.
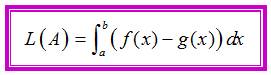
☀ Luas daerah antara dua kurva yang berpotongan di tengahnya
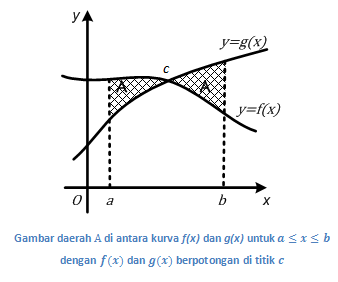
Misalkan A adalah daerah yang dibatasi kurva , , , dan dengan dan berpotongan di dengan sehingga untuk , dan untuk . Luas daerah A yang dilambangkan dengan L(A) dapat kita hitung dengan integral berikut.
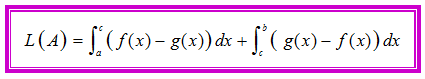
☀ Luas daerah antara dua kurva yang berpotongan di beberapa titik yang bukan titik ujungnya
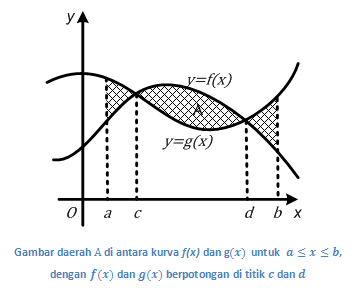
Misalkan A adalah daerah yang dibatasi kurva , , , dan dengan dan berpotongan di dan dengan sehingga untuk , dan untuk , dan untuk . Luas daerah A yang dilambangkan dengan L(A) dapat kita hitung dengan integral berikut.
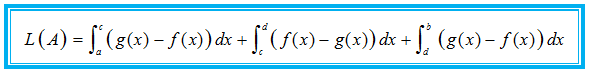
▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩
Oleh karena terdapat empat kasus di atas, maka untuk menentukan rumus yang akan digunakan, kamu perlu memperhatikan hal-hal berikut.
☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲
𝟙. Jika gambarnya diketahui
Jika gambarnya diketahui, maka cukup perhatikan posisi fungsi dan selangnya untuk menentukan batas dan rumus yang akan digunakan.
♫ Contoh 1
Perhatikan gambar di bawah ini.
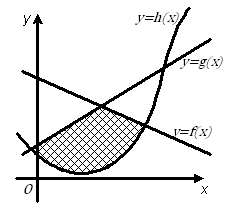
Jika diketahui dan berpotongan di titik , dan berpotongan di titik , dan dan berpotongan di titik di bagian kiri dan di bagian kanan, maka rumus untuk menghitung luas daerah yang diarsir adalah ….
Jawab:
Tambahkan keterangan pada absis dari masing-masing titik potong seperti gambar di bawah ini.
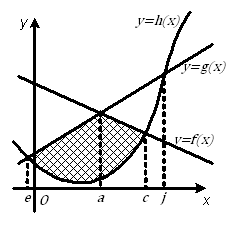
Perhatikan bahwa untuk , kurva di atas atau . Untuk , kurva di atas atau . Dengan demikian, luas daerah yang diarsir pada gambar adalah:
𝟚. Jika hanya fungsinya yang diketahui
Jika hanya fungsi kedua kurva saja yang diketahui, maka untuk menghitung luas daerah tersebut dapat dilakukan dengan langkah-langkah berikut.
Misalnya terdapat fungsi dan .
➤ Tentukan titik potong kedua fungsi dengan menentukan solusi dari persamaan
➤ Perhatikan apakah titik potong tersebut masuk dalam interval pengintegralan (selang )
- Jika tidak, tentukan nilai fungsi mana yang lebih besar antara dengan . Nilai fungsi yang lebih besar berarti fungsi tersebut di atas fungsi lain sehingga integralnya bertanda positif.
- Jika ya, bagilah (partisilah) selang dengan titik potong tersebut. Misalkan titik potongnya adalah dan , maka untuk setiap selang , , dan tentukan nilai fungsi yang lebih besar antara dengan . Nilai fungsi yang lebih besar berarti fungsi tersebut di atas fungsi lain sehingga integralnya bertanda positif.
➤ Gunakan rumus integral luas yang sesuai dengan permasalahan pada soal untuk menghitung luas daerah tersebut.
☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲
Untuk lebih memahami cara menentukan luas daerah yang dibatasi dua kurva, perhatikan contoh berikut ini.
Contoh 1
Luas daerah yang dibatasi oleh kurva , , , dan adalah ….
Jawab:
Oleh karena pada soal hanya diketahui fungsinya, maka ikuti langkah berikut ini.
➤ Tentukan titik potong kedua kurva
Substitusi y = x ke y = x3 , sehingga diperoleh:
➤ Perhatikan bahwa ketiga titik potong tersebut tidak berada dalam selang dan untuk , sehingga luas daerah yang dibatasi kedua kurva tersebut adalah:
Jadi, luas daerah tersebut adalah 54 satuan luas.
Contoh 2
Luas daerah yang dibatasi oleh kurva dengan kurva adalah ….
Jawab:
Oleh karena pada soal hanya diketahui fungsinya, maka ikuti langkah berikut ini.
➤ Tentukan titik potong kedua kurva
Substitusi y = 7 - x2 ke y = x2 - 2x + 3, sehingga diperoleh:
➤ Oleh karena kurva berpotongan di x = -1 dan x = 2, maka batas integralnya adalah -1 ≤ x ≤ 2. Selanjutnya, periksalah manakah fungsi yang lebih besar di antara kedua fungsi tersebut. Caranya, cukup ambil satu titik uji dalam selang tersebut dan substitusikan pada masing-masing fungsi, misalkan x = 0.
Ini berarti, untuk .
Dengan demikian, luas daerah yang dibatasi kedua kurva tersebut adalah:
Jadi, luas daerah tersebut adalah 9 satuan luas.
Contoh 3
Luas daerah yang dibatasi oleh kurva , , , dan adalah ….
Jawab:
Perhatikan gambar berikut.
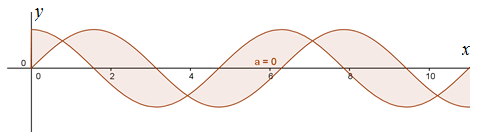
Mula-mula, tentukan titik potong antara kedua kurva.
Untuk , diperoleh .
Oleh karena titik potong berada dalam selang pengintegralan, maka bagilah selang tersebut menjadi 2 bagian. Kemudian, periksalah manakah fungsi yang lebih besar di antara kedua fungsi pada selang tersebut.
Untuk dan untuk
Dengan demikian, luas daerah yang dibatasi oleh kurva , , dan adalah:
Jadi, luas daerah tersebut yaitu satuan luas.
Nah, kamu telah selesai belajar tentang luas daerah yang dibatasi oleh dua kurva. Agar pemahamanmu bertambah lagi, yuk kerjakan latihan soal-soal berikut ini. Selamat