Apabila pusat lingkaran adalah (a,b). Maka semua titik-titik yang berjarak r dari titik pusat (a,b) akan membentuk sebuah lingkaran.
Mari sekarang kita turunkan persamaan lingkaran.
Kita buat sebuah segitiga di dalam lingkaran seperti yang ditunjukkan pada gambar di bawah ini.
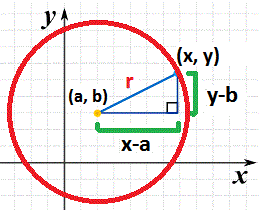
Dengan menggunakan teorema Pythagoras(a2 + b2 = c2), kita dapatkan:
(x-a)2 + (y-b)2 = r2
yang merupakan "BENTUK BAKU PERSAMAAN" dari sebuah lingkaran.
Seringkali persamaan lingkaran tidak diberikan dalam bentuk baku seperti ini. Mari kita mulai dari bentuk baku persamaan yang kemudian dijabarkan sebagai berikut.
(x-a)2 + (y-b)2 = r2
x2 + a2 -2ax + y2 + b2 - 2by = r2
x2 + y2 - 2ax - 2by = r2 - a2 - b2
x2 + y2 - 2ax - 2by = r2 - a2 - b2
x2 + y2 - 2ax - 2by + c = 0
di mana c = √(a2 + b2 - r2)
Persoalan berikut ini adalah tentang menggunakan persamaan lingkaran untuk menemukan titik pusat dan jari-jari lingkaran. Berikut ini adalah beberapa contoh yang akan membantu kita dalam memahami konsep.
CONTOH 1:
Carilah persamaan lingkaran yang berpusat di (4,-3) dan mempunyai keliling 10π?
PENYELESAIAN:
kita ketahui bahwa keliling lingkaran dinyatakan dengan
C = 2πr
Karena diketahui keliling lingkaran adalah 10π, maka kita dapatkan r = 5 units
Jadi, persamaan lingkaran yang didapatkan adalah:
(x-4)2 + (y+3)2 = 52
CONTOH 2:
Carilah persamaan lingkaran yang mempunyai (2, 4)dan (-2, 0) sebagai titik-titik akhir dari diameternya.
PENYELESAIAN:
Pusat lingkaran akan terletak pada titik pertengahan diameternya.
Jadi,
titik pusat = ( (2-2)/2 , (4+0)/2 ) = (0, 2)
Dengan menggunakan rumus jarak, jari-jari 'r' dapat ditemukan seperti dibawah ini:
r = √{ (2-0)2 + (4-2)2 } = 2√2
Jadi persamaan lingkaran yang didapatkan adalah:
(x-0)2 + (y-2)2 = (2√2)2
ATAU x2 + y2 -4y = 8