Lingkaran dan kesebangunan

Lingkaran dan kesebangunan - Semua benda di sekitar kita dapat didefinisikan dalam 2 faktor, yaitu : bentuk dan ukuran. Dua benda dengan bentuk yang sama dikatakan serupa. Selanjutnya, karena dua benda tersebut serupa, maka ukuran keduanya adalah sama. Dengan demikian, keduanya dikatakan kongruen atau sama.

Lingkaran adalah gambar geometris yang terdiri atas himpunan titik yang berjarak sama jika diukur dari titik pusat. Seperti halnya bujur sangkar, namun berbeda dengan segitiga maupun jajar genjang, lingkaran hanya berbeda dalam hal ukuran.

Selanjutnya, dengan memperhatikan sifat-sifat bentuk, nilai numerik yang diperoleh dari beberapa lingkaran adalah sama. Sebagai contoh : garis keliling dari satu lingkaran penuh (Keliling lingkaran : K), nilainya bergantung pada diameter lingkaran (d). Hal ini selalu berlaku untuk semua lingkaran.

Selanjutnya, keberadaan π sebagai suku dalam persamaan K = πd dilandaskan pada kenyataan bahwa semua lingkaran adalah serupa dan mempunyai bentuk yang sama. Adapun, nilai π ini dapat diestimasi dengan cara sebagai berikut :

1. Gambarlah 2 buah lingkaran dengan diameter berbeda.
2. Hitunglah panjang diameternya dengan menggunakan penggaris.
3. Hitunglah keliling dari kedua lingkaran dengan tali/senar.
4. Carilah rasio antara keliling dan diameter dari masing-masing lingkaran.

Perhatikan contoh berikut :

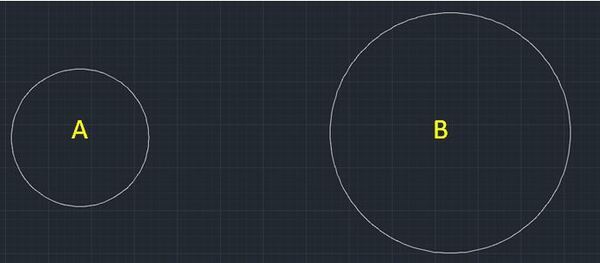
1. Lingkaran A mempunyai diameter 8 cm, sedangkan lingkaran B mempunyai diameter 14 cm.
   
   3. Dengan menggunakan tali/senar dan penggaris dengan akurasi sampai satu desimal, kalian akan memperoleh keliling lingkaran A = 25,1 cm dan keliling lingkaran B = 44 cm.
   
   4. Rasio antara keliling dan diameter dari masing-masing lingkaran adalah sebagai berikut :

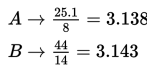
Seperti yang kalian lihat, nilai yang diperoleh hampir sama. Pada kenyataannya, jika kita menghitungnya sampai 2 desimal, kita akan memperoleh nilai 3,14. Jika cara pengukuran yang lebih akurat telah tersedia (memungkinkan), maka kita akan mendapatkan hasil yang sama dengan 3,14. Lebih lanjut, nilai ini dikenal dengan nama pi (π =3,14). Sebagai catatan, percobaan di atas juga dapat dilakukan dengan menggunakan dua lingkaran yang lain, untuk melihat apakah kedua lingkaran tersebut memberikan hasil yang sama.