Lingkaran didefinisikan sebagai the himpunan semua titik yang mempunyai jarak sama jika diukur dari titik pusat.
Jika titik pusat lingkaran adalah (a,b), maka semua titikyang mempunyai jarak sebesar r jika dihitung dari titik pusat (a,b) akan membentuk sebuah lingkaran.
Mari kita turunkan persamaan lingkaran dengan cara sebagai berikut :
Buatlah sebuah segitiga siku-siku di dalam sebuah lingkaran, seperti yang ditunjukkan oleh gambar di bawah ini.
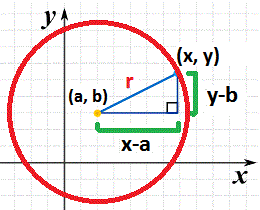
Dengan menggunakan theorema Phytagoras : (a2 + b2 = c2), diperoleh :
(x-a)2 + (y-b)2 = r2
yang mana merupakan"PERSMAAN LINGKARAN SECARA UMUM (BENTUK STANDAR)".
Catatan : seringkali persamaan lingkaran yang diberikan tidak dalam bentuk standar. Selanjutnya, dengan menjabarkan bentuk kuadrat dari persamaan lingkaran secara umum, maka diperoleh :
(x-a)2 + (y-b)2 = r2
x2 + a2 -2ax + y2 + b2 - 2by = r2
x2 + y2 - 2ax - 2by = r2 - a2 - b2
x2 + y2 - 2ax - 2by = r2 - a2 - b2
x2 + y2 - 2ax - 2by = c2
dimana c2 = r2 - a2 - b2
Dalam pelajaran ini, kalian akan belajar tentang bagaimana mencari persamaaan persamaan lingkaran jika diketahui jari-jari lingkaran atau titik pusat. Berikut ini adalah beberapa contoh yang akan membatu kalian dalam memahami materi ini :
CONTOH 1 :
Carilah persamaan lingkaran dengan titik pusat (4, -3) dan keliling sebesar 10π!
PENYELESAIAN :
Seperti yang telah kita ketahui, keliling lingkaran adalah
K = 2πr
Karena keliling lingkaran adalah 10π, maka r = 5 satuan panjang.
Dengan demikian. persamaan lingkaran yang dicari adalah :
(x-4)2 + (y+3)2 = 52
CONTOH 2 :
Carilah persamaan lingkaran yang terbentuk jika diketahui titik-titik ujung dari diameter lingkaran adalah (2, 4) dann(-2, 0)!
PENYELESAIAN :
Titik pusat lingkaran akan berada pada titik tengah dari diameter lingkaran.
Dengan demikian,
titik pusat lingkaran = ( (2-2)/2 , (4+0)/2 ) = (0, 2)
Selanjutnya, dengan menggunakan rumus jarak, panjang jari-jari lingkaran (r) dapat dicari dengan cara sebagai berikut :
r = √{ (2-0)2 + (4-2)2 } = 2√2
Jadi, persamaan lingkaran yg dicari adalah :
(x-0)2 + (y-2)2 = (2√2)2
ATAU x2 + y2 -4y = 8